关键路径 学习笔记
首先需要理解AOE网络，它表示的含义是，网络中的每个节点表示一个事件，每条边表示一个活动。

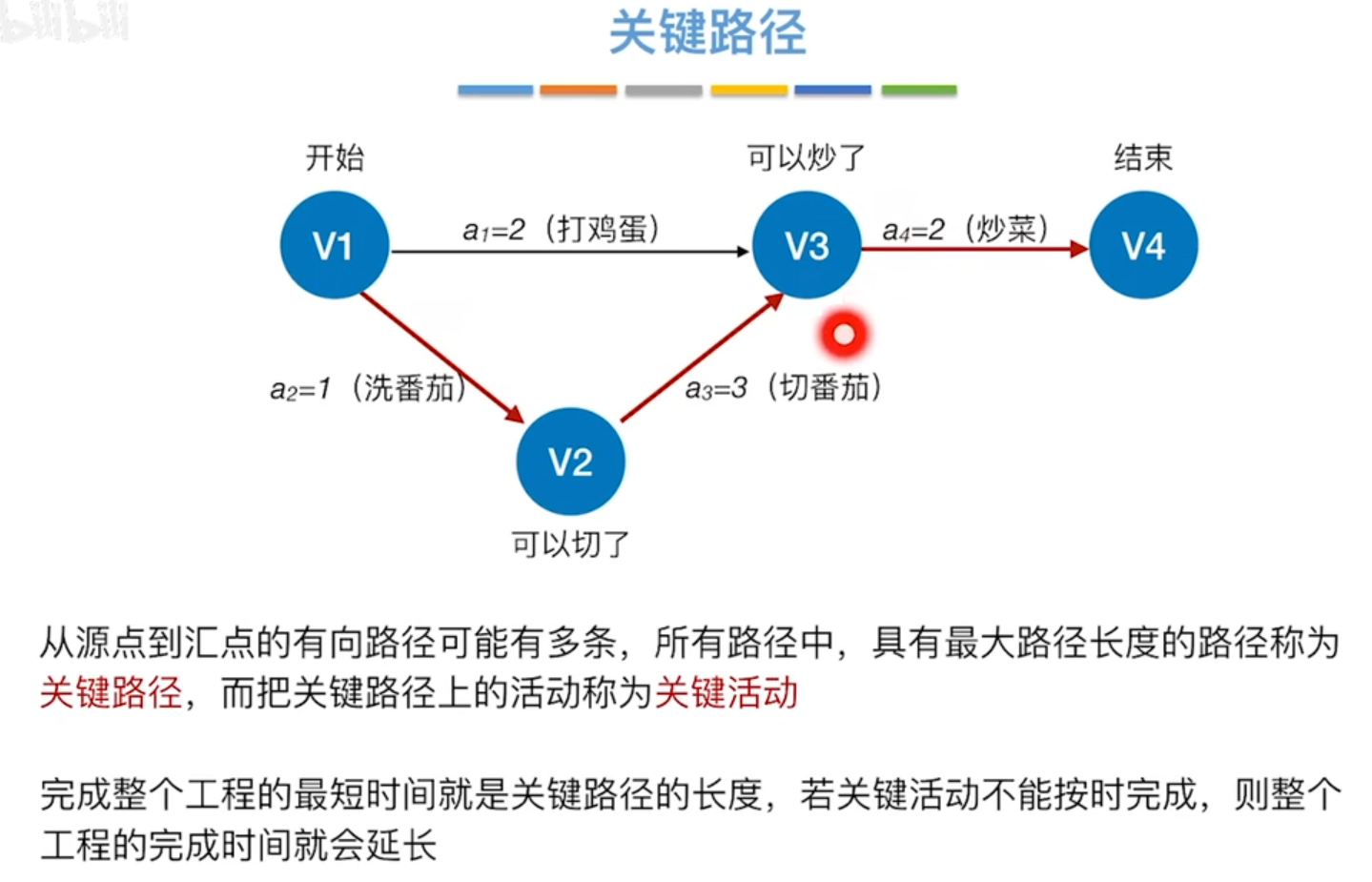
AOE网络中，当然还涉及到一些概念，关键路径，关键活动，关键活动的性质。
接着，对于给定的AOE网络，如何求解关键活动，关键路径呢？
举个例子：

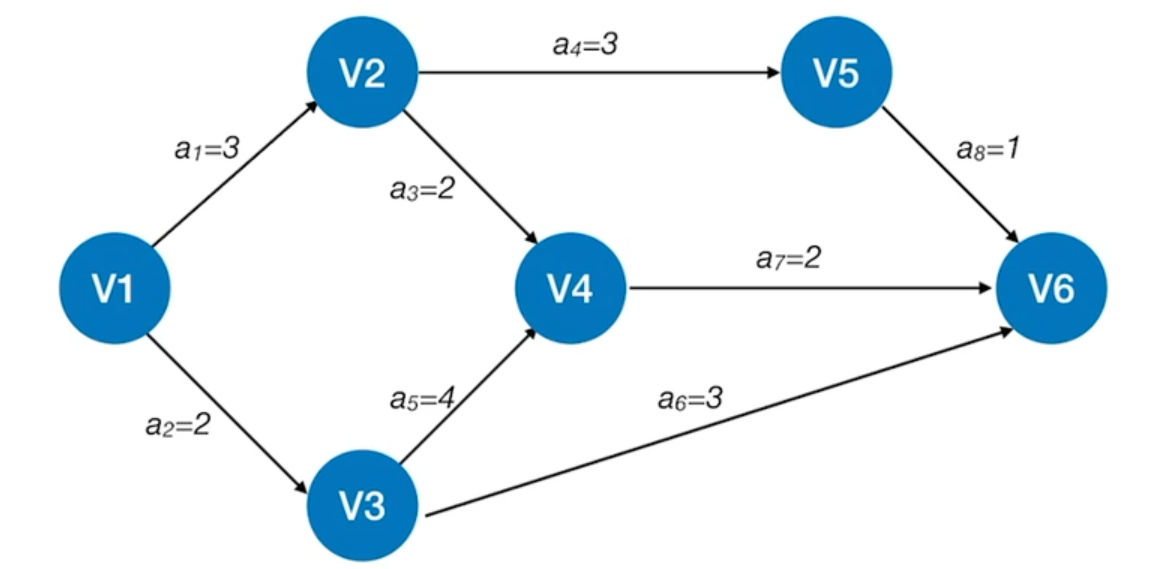
对于给定的AOE网络，求解关键活动和关键路径非常的简单。
步骤：
1. 求解每个事件(节点)的最早发生时间。
2. 求解每个事件(节点)的最迟发生时间。
3. 求解每个活动(边)的最早发生时间。
4. 求解每个活动(边)的最迟发生时间。
5. 计算每个活动的时间余量，余量为0的活动就是关键活动。

具体而言，对于步骤(1)：
1.求得原图的拓扑序列，按照拓扑序列来求可以保证结果的正确性。
2.将源点最早发生时间记为0
3.对于任意节点$v_{k}$,依照递推公式$v_{k}$ = $max$ { $v_{j} + w_{jk}$} 其中，$j$是$k$的前驱。
表示的含义是当事件$k$的前驱事件全部被处理完，事件$k$才能开始。

对于步骤(2):
1.按照拓扑序列的逆序列求解，对于汇点(终点)而言，最迟开始时间等于最早开始时间
2.按照递推公式，对于任意的节点$v_{k}$,$v_{k}$ = $min$ { $v_{j} - w_{kj}$}, 其中，$j$是$k$的后继。

对于步骤(3):
对于任意活动$a_{i}$,它的开始时间等于 该活动对应的边的尾部(箭头段的另一侧)所指的事件的最早开始时间。
画个图 简单明了

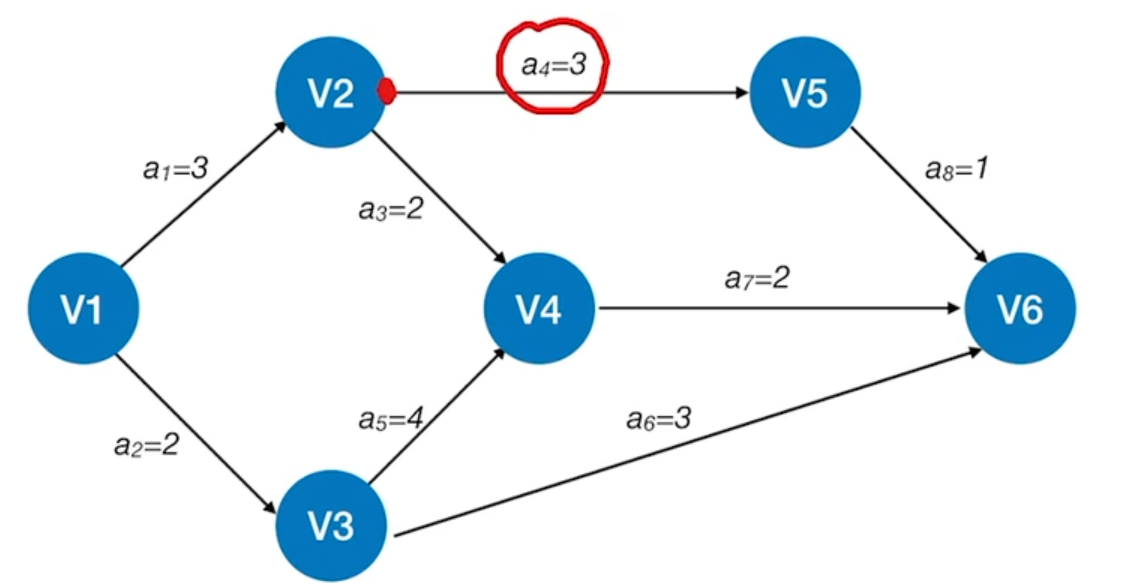
活动$a_{4}$的最早发生时间 等于 事件$v_{2}$的最早发生时间。

对于步骤(4)：
利用事件的最迟发生时间，以及活动的持续时间。它依赖于该活动尾部所指的事件。举个例子

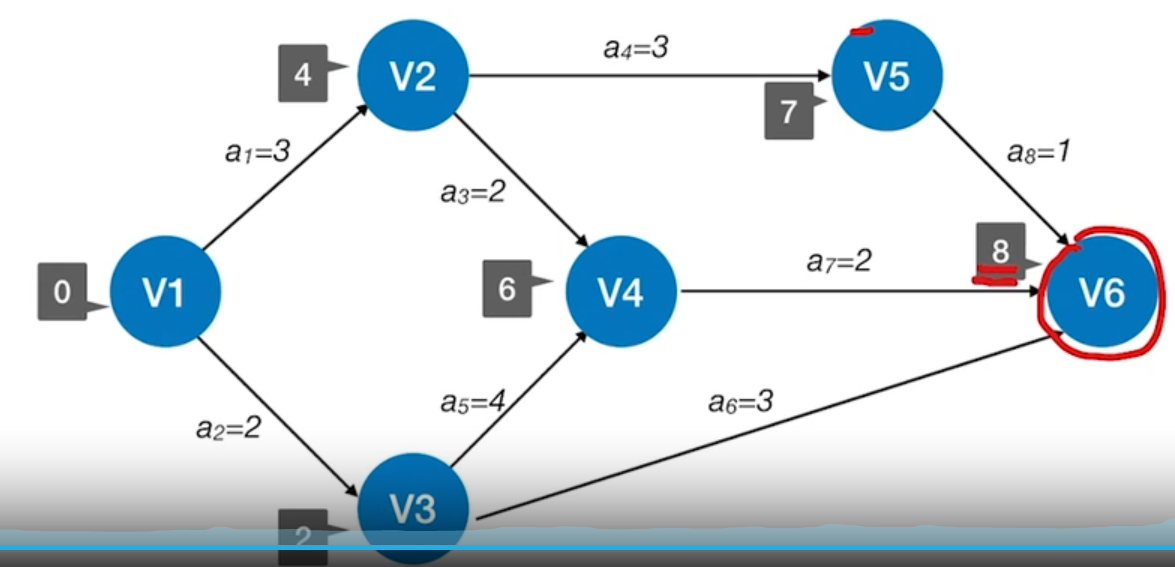
对于活动$a_{8}$,它的持续时间$t_{1}$是1,它指向的事件是$v_{6}$最晚发生时间记为$t_{2}$
那么，活动$a_{8}$的最迟开始时间$t = t_{2} - t_{1} $

对于步骤(5):
利用活动的最迟开始时间-活动的最早开始时间，为0的活动就是关键活动，关键活动构成的路径就是关键路径。