求N中所有与N互质的个数
N可以表示成N = p1^a1 + p2^a2 ... pk^ak(p1-pk是N的质因子)
1.从1-N中去掉多有p1 , p2 , p3 ... pk 的倍数
2.由于一个数可能是p1和p2 ， p1 和p3 .... pi 和pj的倍数 他们都被减掉了2次
所以再加上pi * pj 的倍数
3.如果一个数是p1p2p3的倍数，他会先被p1减一次 ， p2减一次 ，p3减一次
然后被p1p2的倍数加一次，p1p3的倍数加一次,p2p3的倍数加一次 ，等于没有减没有加
所以我们还需要减去pipjpk的倍数 以此类推 看下图

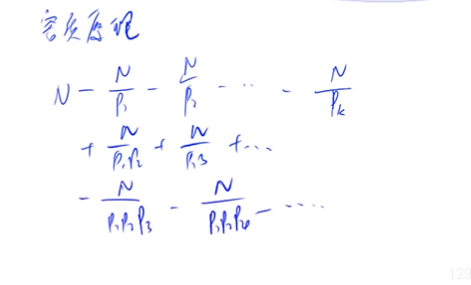
上面的式子就是1-N中所有与N互质的个数
整理一下：
h(x) = N(1 - 1/p1)*(1 - 1/p2)*(1 - 1/p3)...(1 - 1/pk)
求欧拉函数的时间复杂度上界在分解质因数：O(根号n)

res = res * (1 - 1 / p1) 式子里不能有小数 所以通分得 res / p1 * (p1 - 1)

欧拉定理证明 看下图: