1.图的定义与子图

图的定义:图(Graph简写G)G由顶点集V和边集E组成,记作G=(V,E),其中V(G)表示图G中顶点的有限非空集;E(G)表示图G中顶点之间的关系(边)集合。若V= {v1,2,…,vn},则用|V|表示图G中顶点的个数,E= {(u,v)|u∈V, v∈},用|E|表示图G中边的条数。
ps:树可为空树,线性表可为空表,图不能为空图！！ 因为若图为空,则顶点集合V也为空 而V必须是是有限非空集合。但边集合E可以为空,此时,图就是只有点没有边。
子图:设有两个图,G=(V,E)和G’=(V’,E’),若V’是V的子集 且 E’是E的子集，则称G’是G的子图。
ps:Q：设有图G=(V,E),若V’是V的子集 E’是E的子集 V’和E’能构成G(V,E)的子图吗？
A:不一定,若E’的边中有顶点不存在于V’则连图都无法构成 何谈子图

2.完全图与有向完全图

完全图:有n(n-1)/2条边的无向图
有向完全图:有n(n-1)条边的有向图

3.连通与强连通

连通:无向图中,顶点v到顶点w有路径
强连通:有向图中,顶点v到顶点w和顶点w到顶点v都有路径

4.连通图与强连通图

连通图:无向图中,任意二点都是连通的。
强连通图:有向图中,任意二点都是强连通的。

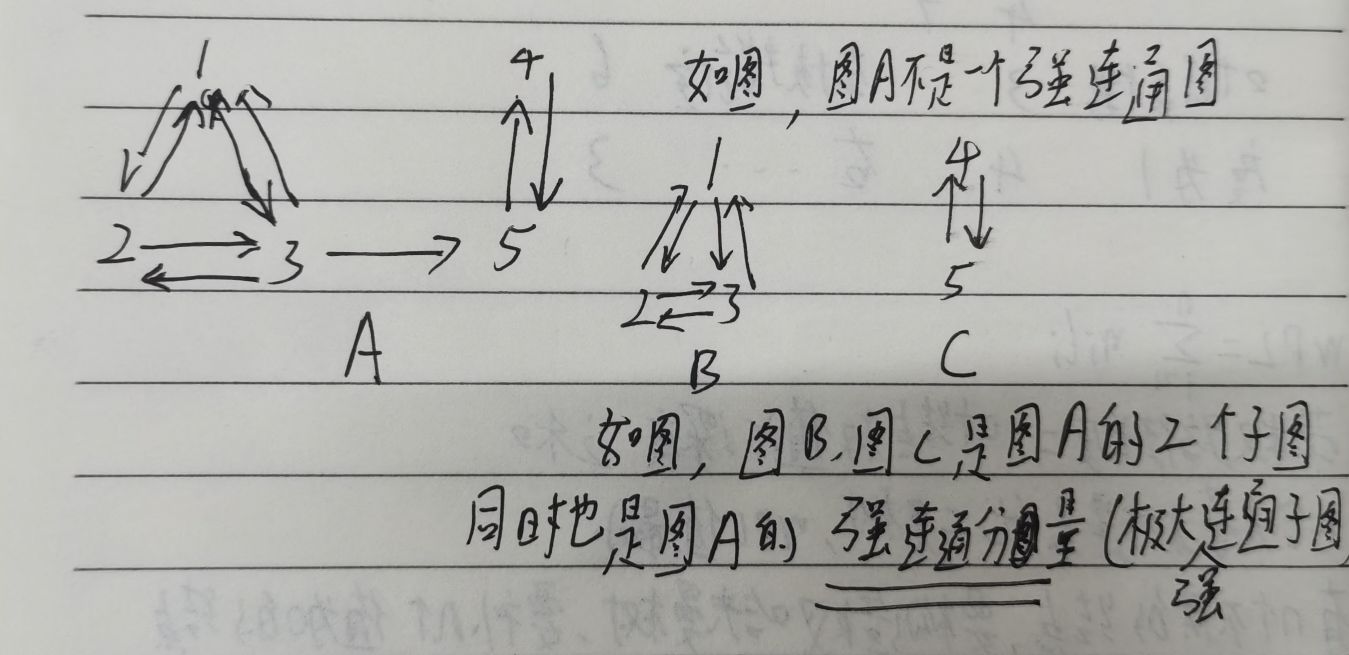
5.连通分量,极大连通子图,极小连通子图

连通分量就是极大连通子图。
极大:指包含该连通子图的所有边
极小连通子图:连通图的生成树,既要保证图的连通,又要注意边数最小,若有n个顶点,则只能有n-1条边

注意事项：此处的图指的都是无向图,无向图讨论连通性,有向图讨论强连通性。

Q1:有n个顶点的无向连通图 其边的数量最少为多少
A1:构成一棵树 n-1条边

Q2:有n个顶点的有向强连通图 其边的数量最少为多少
A2:构成一个有向环 n条边

Q3:若有无向图G=(V,E),G有n个顶点,请问至少要多少条边能确保G是连通图
A3:取n-1个点 将其构造成完全图 再加一条边将第n个点与完全图连接 共计(n-2)*(n-1)/2+1条边

6.邻接表 邻接矩阵存什么图

邻接表一般存稀疏图。
邻接矩阵一般存稠密图，同时由于对称,可以压缩存储,只存主对角线以上或以下
ps：判断图是否稠密一般是看边的数量|E|是否<$|V|*log_2{|V|}$

7.十字链表 邻接多重链表存什么图

十字链表存有向图
邻接多重表存无向图

8.dfs遍历邻接表与邻接矩阵的时空复杂度

1. dfs遍历邻接表
   时间复杂度:$O(|V|+|E|)$
   空间复杂度:$O(|V|)$
2. dfs遍历邻接矩阵
   时间复杂度:$O(|V|^2)$
   空间复杂度:$O(|V|^2)$

9.bfs遍历邻接表与邻接矩阵的时空复杂度

1. bfs遍历邻接表
   时间复杂度:$O(|V|+|E|)$
   空间复杂度:$O(|V|)$
2. bfs遍历邻接矩阵
   时间复杂度:$O(|V|^2)$
   空间复杂度:$O(|V|^2)$

10.无向图与有向图中顶点的度

无向图中顶点的度:依附顶点v的边的条数
有向图中顶点的度:度=入度+出度 入度=以v为终点的有向边的数目 出度=以v为起点的有向边的数目

11.邻接表与临界矩阵中图顶点的度

1. 邻接表
   有向图:度=入度+出度 出度=以v为顶点表的边表节点数量 入度=含v的边表节点数量
   无向图:度=以v为顶点表的边表节点数量

2. 邻接矩阵
   有向图:度=入度+出度 出度=第i行的非0非无穷元素数量 出度=第i列的非0非无穷元素数量
   无向图:第i行(或列)的非0非无穷元素数量

补丁

简单路径

在路径序列中,顶点不重复出现的路径称为简单路径。