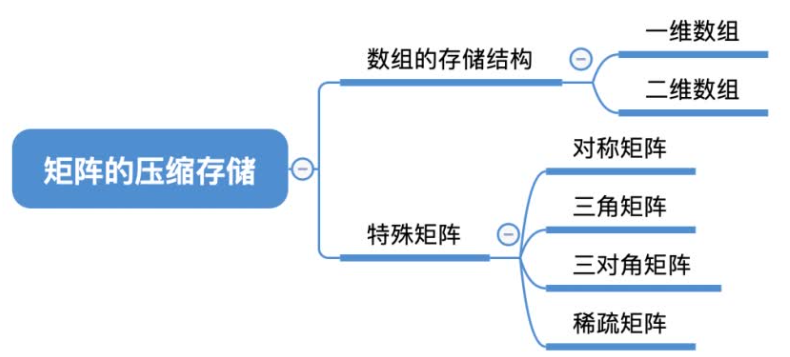
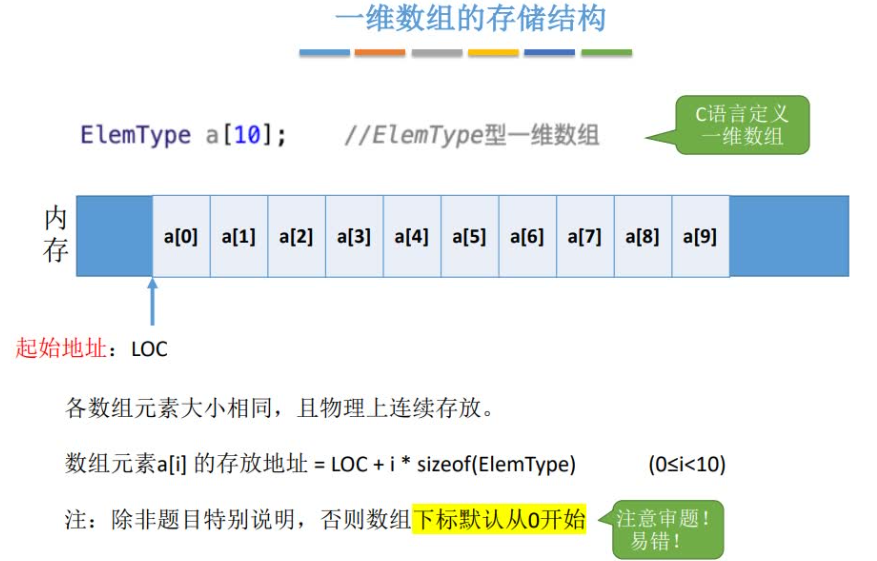
一维数组

一个数组中的所有元素在内存中占用一段连续的存储空间。

二维数组

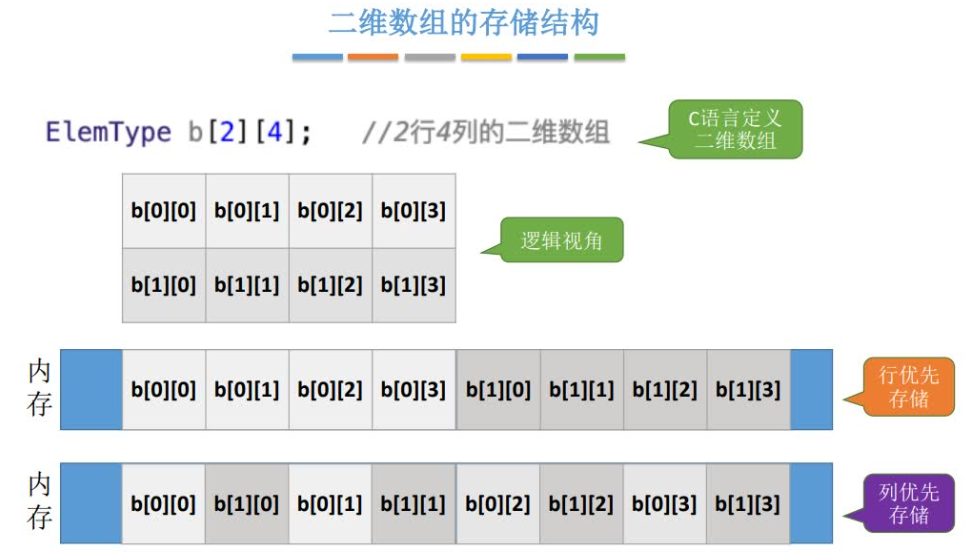
对于多维数组，有两种映射方法：按行优先，按列优先。以二维数组为例：按行优先存储的基本思想是：先行后列，先存储行号较小的元素，行号相等先存储列号较小的元素。

普通矩阵

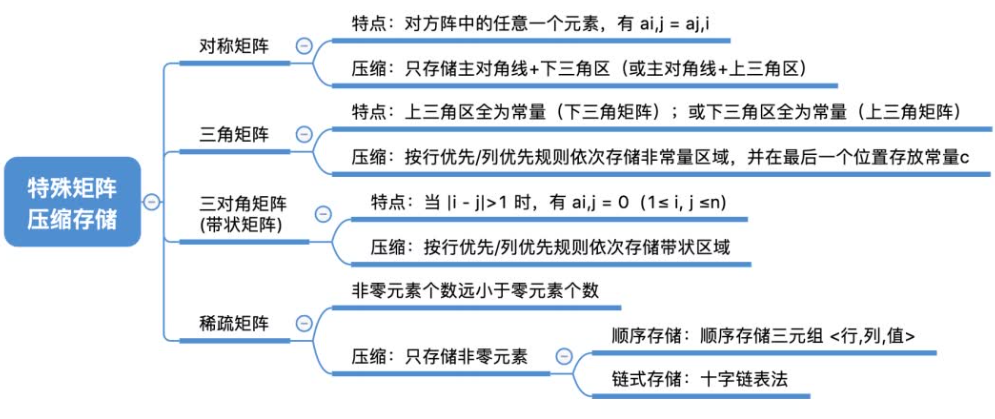
特殊矩阵的压缩存储

压缩存储：指为多个值相同的元素只分配一个存储空间，对零元素不分配存储空间。目的是为了节省存储空间。

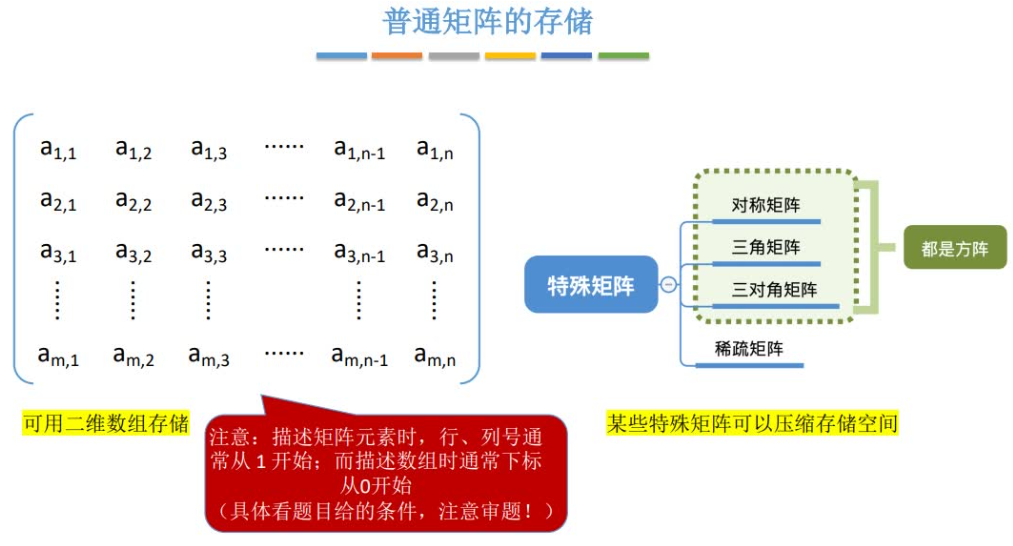
特殊矩阵：指具有许多相同矩阵的元素或零元素，并且这些相同矩阵沿元素或零元素的分布有一定规律性的矩阵。常见的特殊矩阵有 对称矩阵，上（下）三角矩阵，对角矩阵。
注意：它们都是⽅阵，即⾏数和列数相同。

主对⾓线：在矩阵中每个元素的⾏标等于纵标（i==j）。

上三⾓：在矩阵中每个元素的⾏标⼩于纵标（i < j）。

下三⾓：在矩阵中每个元素的⾏标⼤于纵标（i > j）。

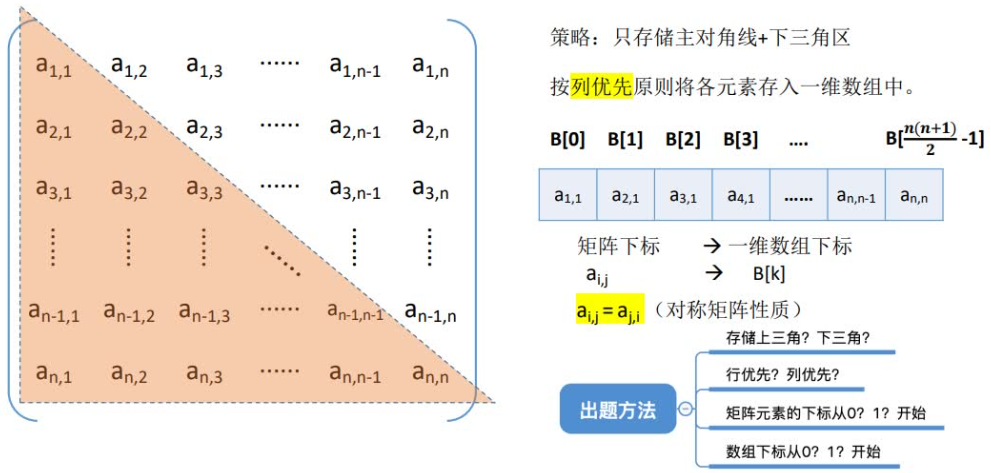
对称矩阵

若一个n阶方阵A[n][n]中的元素满足a i,j=a j,i（0≤i，j≤n-1），则称其为n阶对称矩阵。

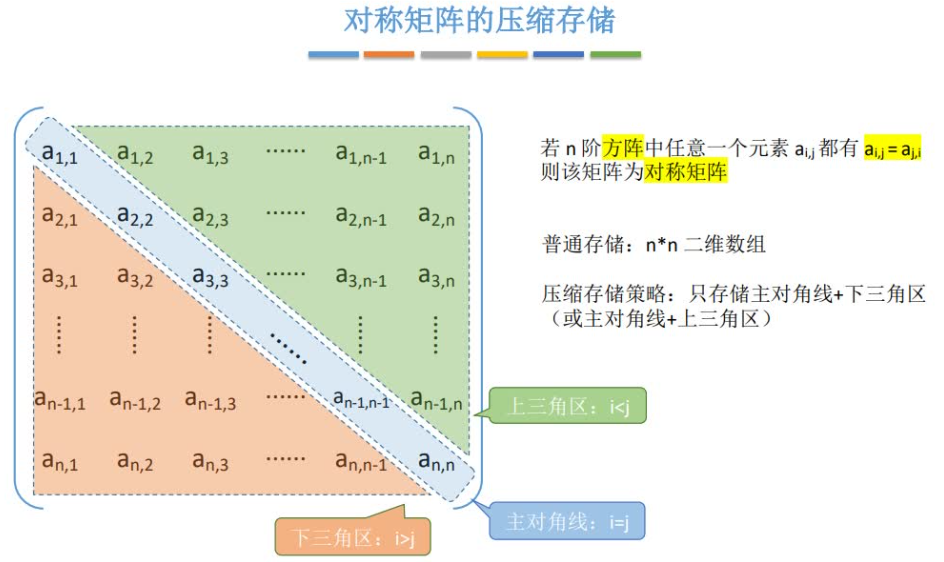
由于对称矩阵中的元素关于主对角线对称，因此在存储时可只存储对称矩阵中上三角或下三角中的元素，使得对称的元素共享一个存储空间。

这样，就可以将n2个元素压缩存储到n(n+1)/2个元素的空间中。以行序为主序存储其下三角＋对角线的元素。

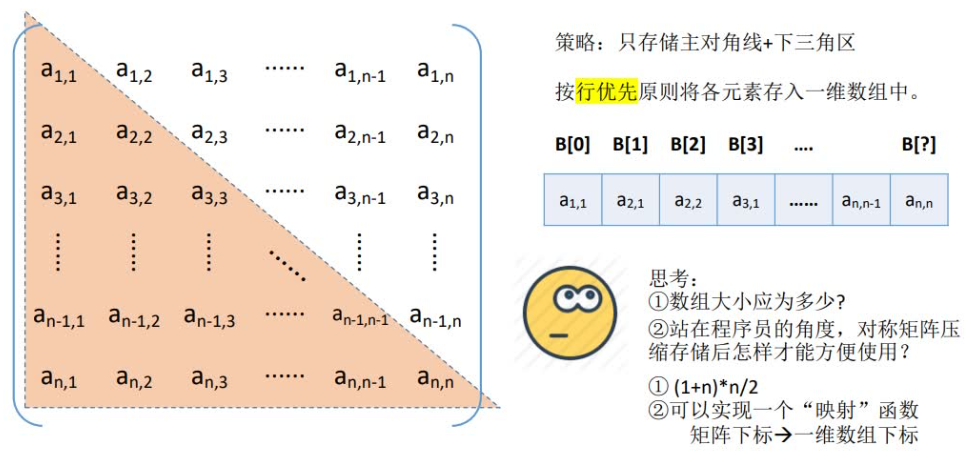
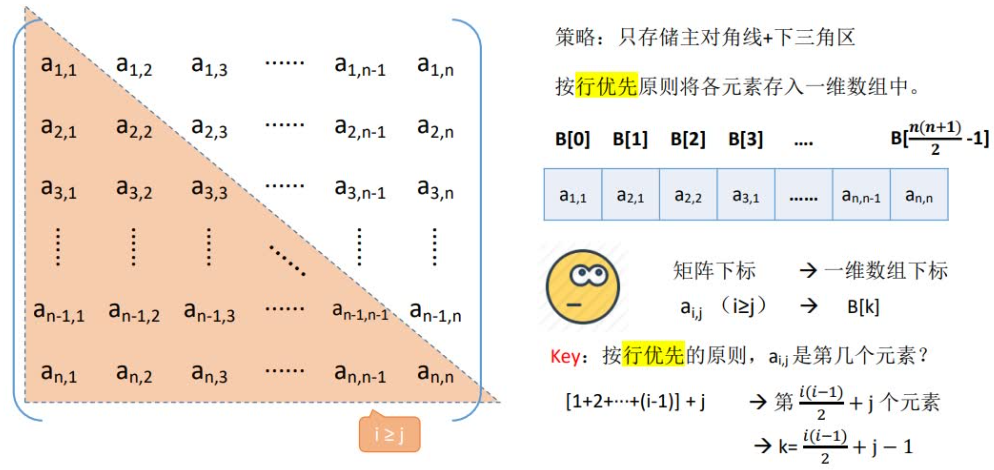
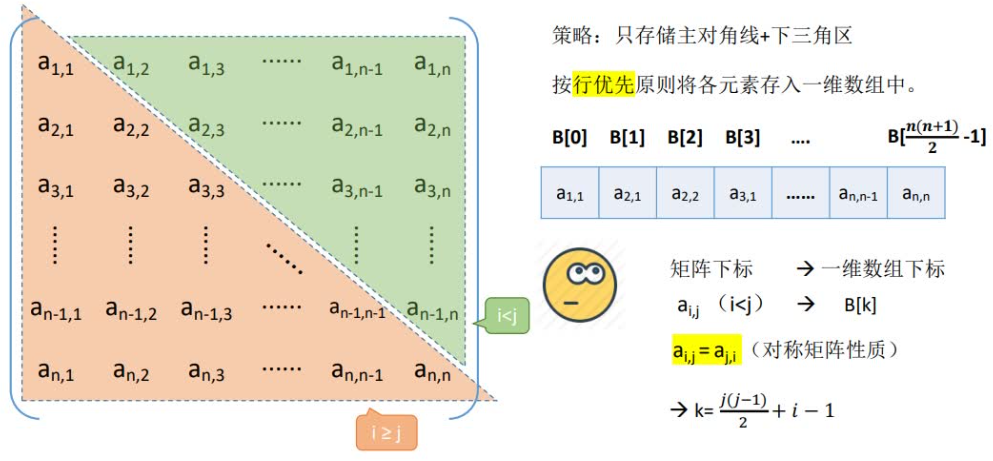
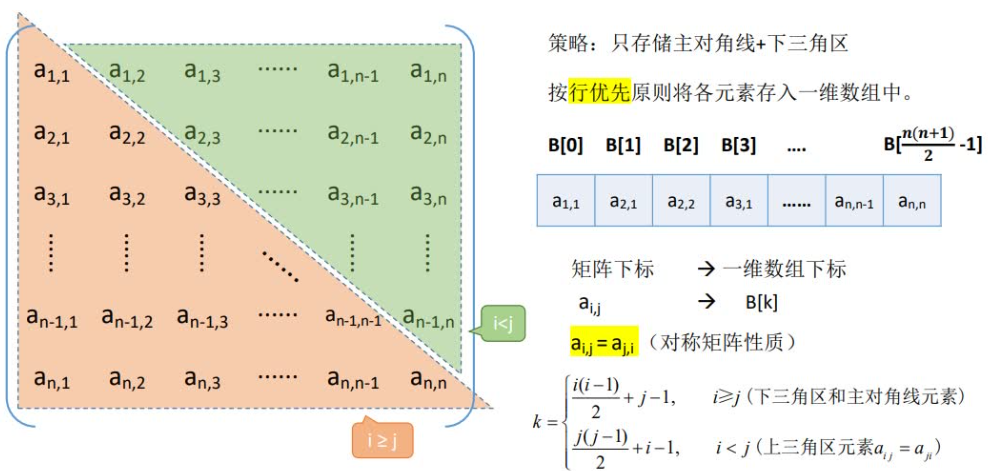
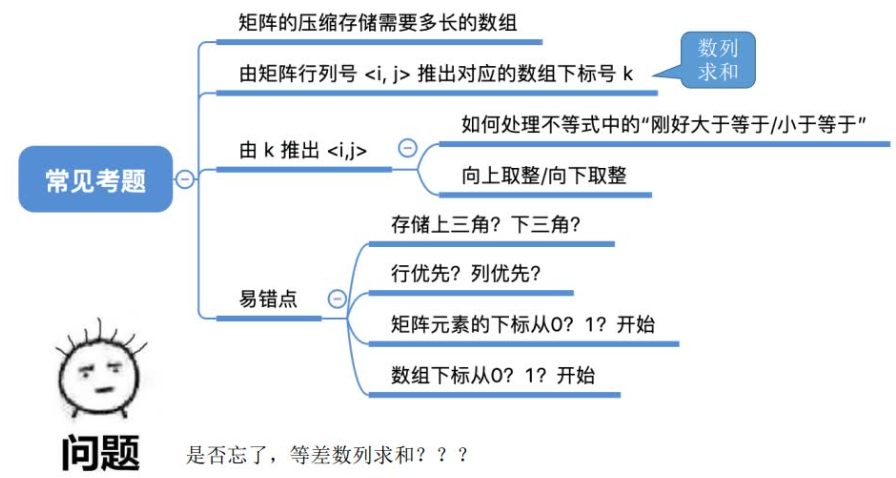
由于k的序号=所有它前⾯元素的个数=所在⾏前⾯⾏的所有元素+所在⾏它前⾯的元素（包括本⾝）。

⼀维数组k与与⼆维数组元素的i、j之间的关系：
当i>=j时，k=i(i+1)/2 + j;//本例都是以0为开始的下标，以下也是类同。
当i<j时，k=j(j+1)/2+i;

三角矩阵

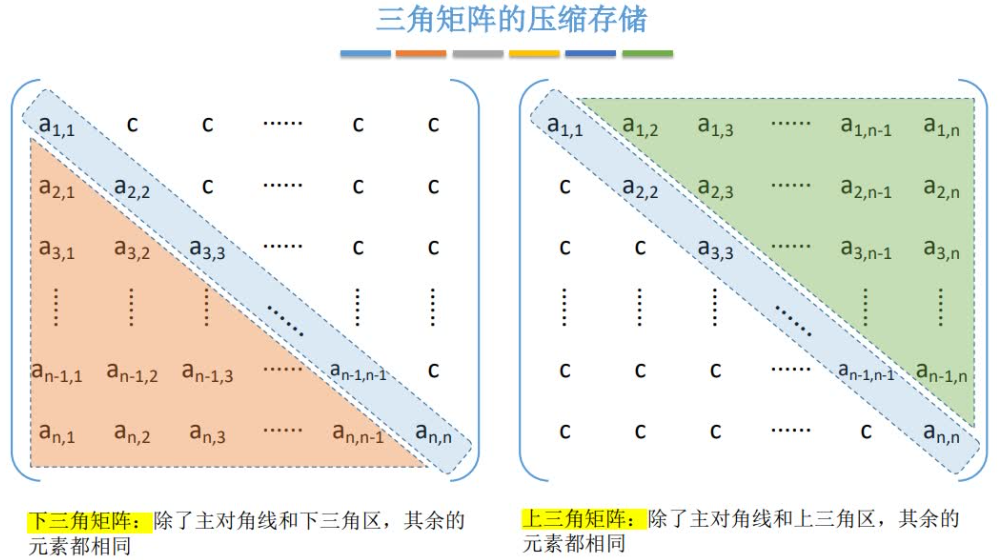
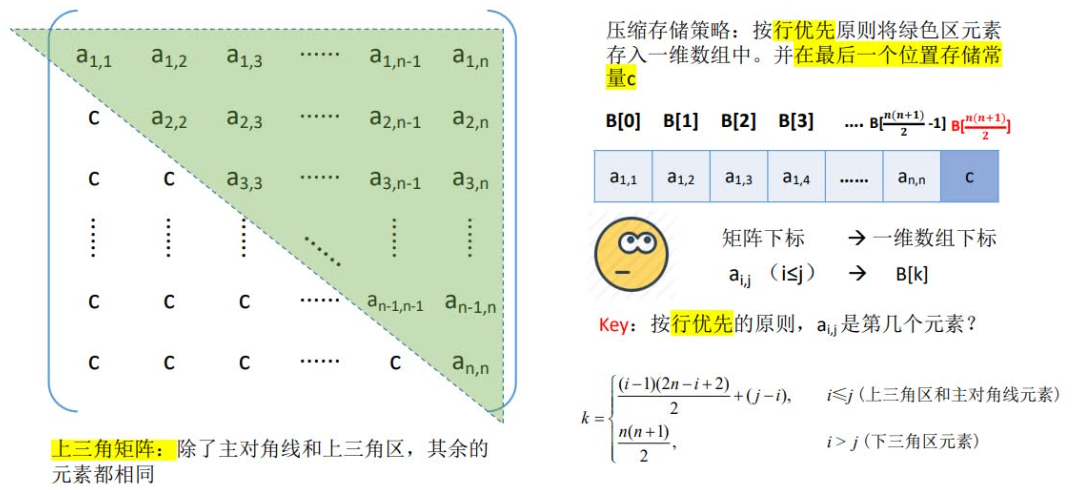
上三⾓矩阵：当⼀个⽅阵的主⾓线以下的所有元素皆为零；
当i< = j 时，k = ( i - 1 ) * ( 2n - i + 2 ) / 2 + j - 2;(以下公式为了⽅便理解，i,j,k都是从1开始)

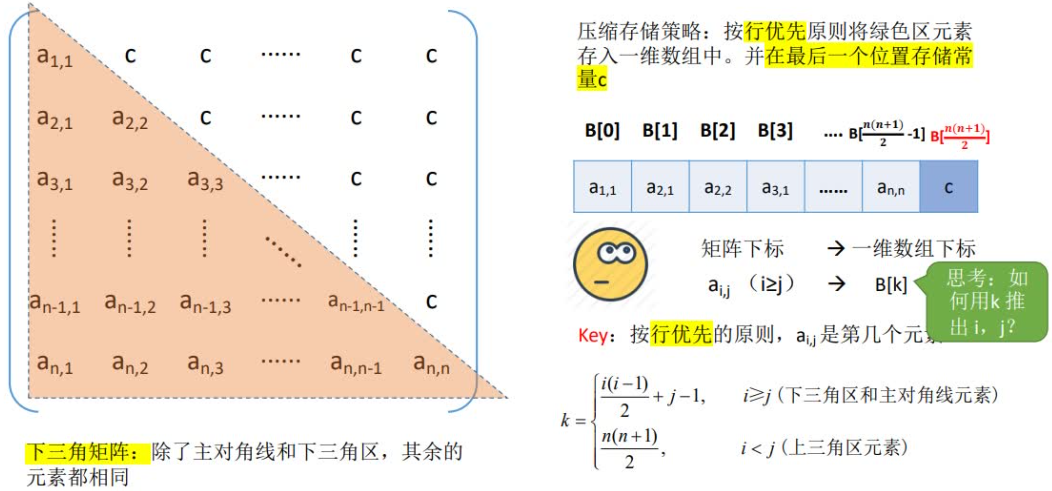
下三⾓矩阵：当⼀个⽅阵的主⾓线以上的所有元素皆为零；
当i > = j时，k = i * ( i + 1 ) / 2 + j - 2;

三对角矩阵

若一个n阶方阵A满足其 所有非零元素 都集中在以主对角线为中心的 带状区域中 ，则称其为 n阶对角矩阵 。
其主对角线上下方各有b条次对角线，称b为矩阵半带宽，(2b+1)为矩阵的带宽。

对于半带宽为b（0≤b≤(n-1)/2）的对角矩阵，其|i-j|≤b的元素ai,j不为零，其余元素为零。

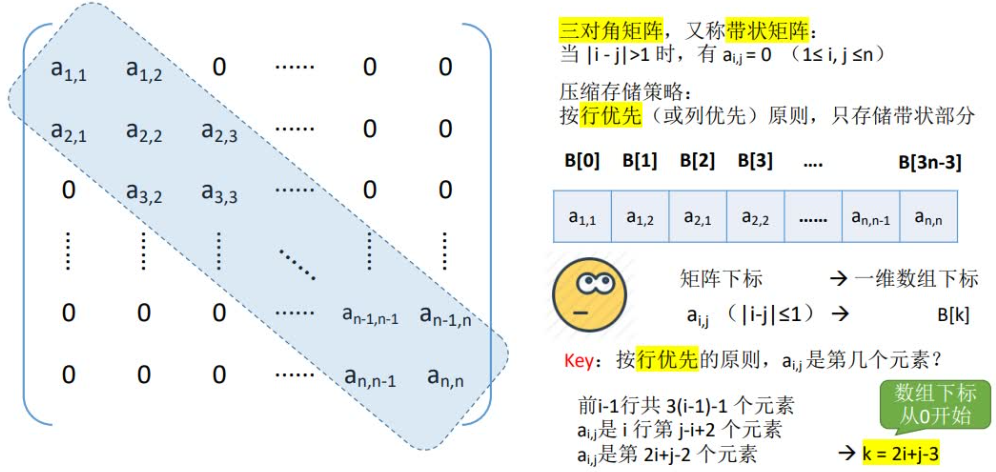
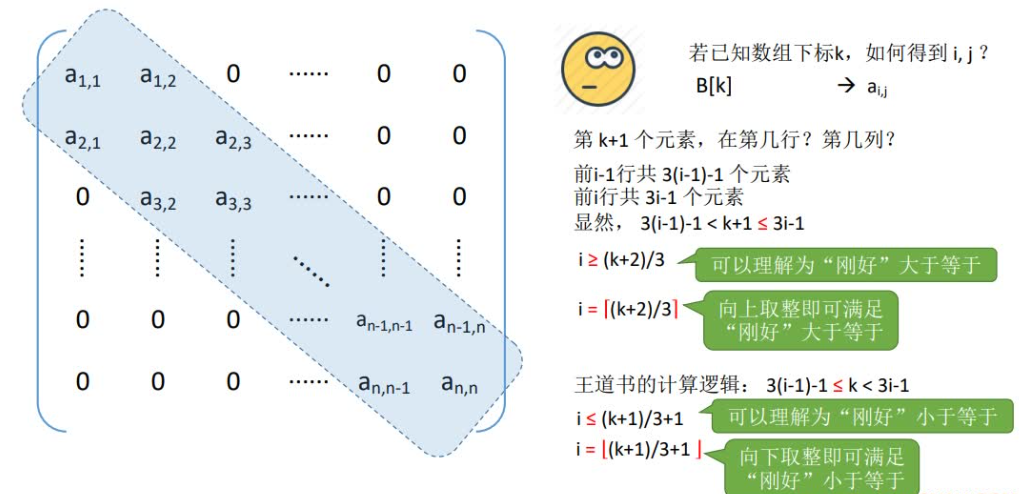
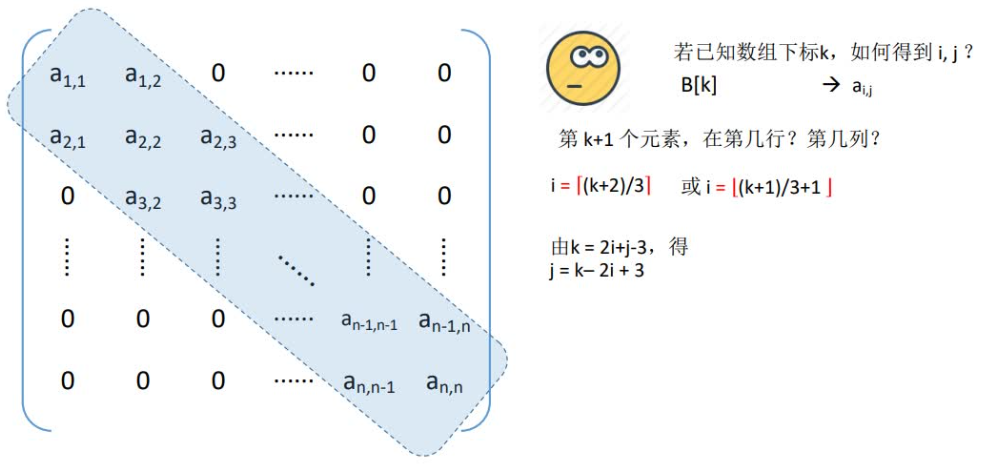
三对角矩阵其压缩地址计算公式如下： k = 2i + j

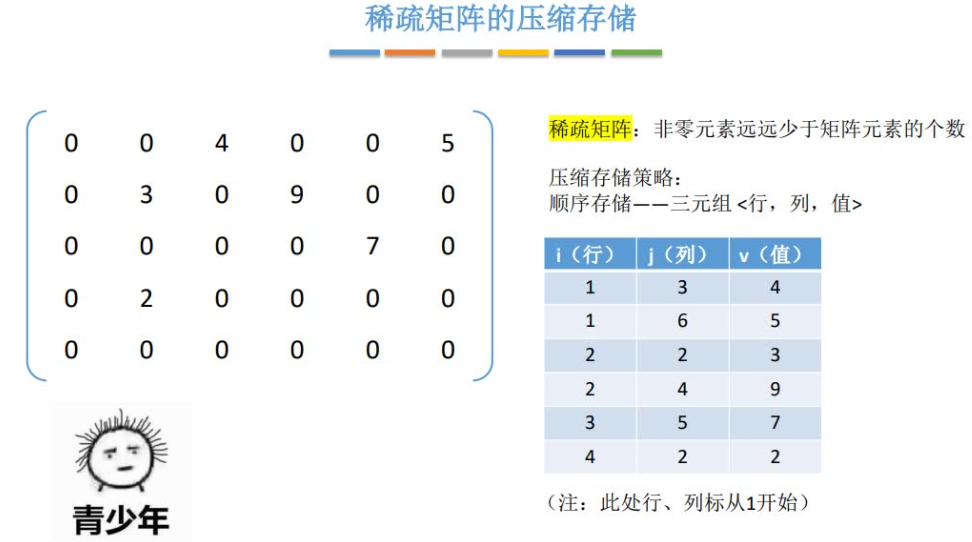
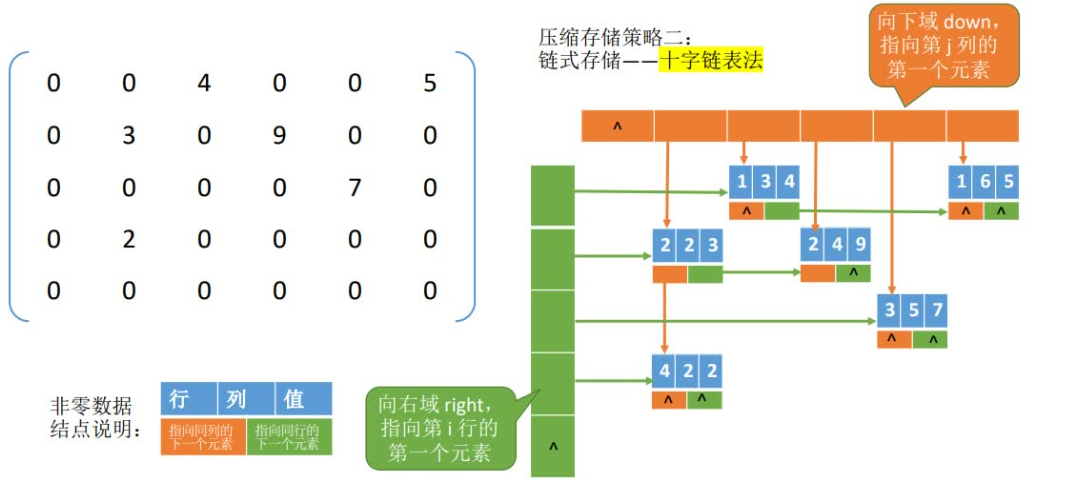
稀疏矩阵

如果矩阵中的非零元素的个数相对整个矩阵的元素个数来说非常少，则将这样的矩阵称为稀疏矩阵。

存储稀疏矩阵，我们一般构造三元组存储矩阵非零元素。系数矩阵压缩存储后便失去了随机存取的特性。

总结