$Least$ $comment$ $ancestors$
$1$. 向上标记法$O(N)$
从$a$开始向上将所有父节点全部标记,然后从$b$开始往上走到的第一个被标记的点,就是最近公共祖先
$2.$ 倍增$O(NlogN)$
$depth[i]$表示每个结点在树中的深度
$fa[i][j]$表示从$i$开始,向上走$2^j$步能走到的结点($0≤j≤logn$)
哨兵:如果从$i$开始条$2^j$会跳到根节点上面(外),那么$fa[i][j]=0$,$depth[0]=0$
跳的时候$k$从大到小才能保证每个$2^j$只选一次
(1) 预处理$f[i][j]$
① $j=0$,即往上跳0步,$fa[i][j]$那么就是$i$的直接父节点
② $j≠0$,那么$f[i][j]=f[f[i][j-1]][j-1]$,即$i$先跳$2^{j-1}$步到达$f[i][j-1]$,再从$f[i][j-1]$跳$2^{j-1}$步,就可以向上跳$2×2^{j-1}$步,即用向上跳两次$2^{j-1}$步算出来了向上跳$2^j$步可以到达的点
(2) $LCA$步骤:
① 先将两个点跳到同一层
② 让两个点同时往上跳,一直跳到他们的最近公共祖先的下一层
因为如果不要求跳到公共祖先的下一层,那么可能a和b同时跳到最近公共祖先的上面的公共祖先,这样就不满足最近的要求了,所以我们判断是否可以往上跳的条件是$fa[a][k] != fa[b][k]$,因为我们不执行最后一步跳0步真正跳到最近公共祖先上的操作,只跳到最近公共祖先的下一层(满足$fa[a][k] != fa[b][k]$),最后要求最近公共祖先只需返回$f[a][0]$即可(再向上跳一步)
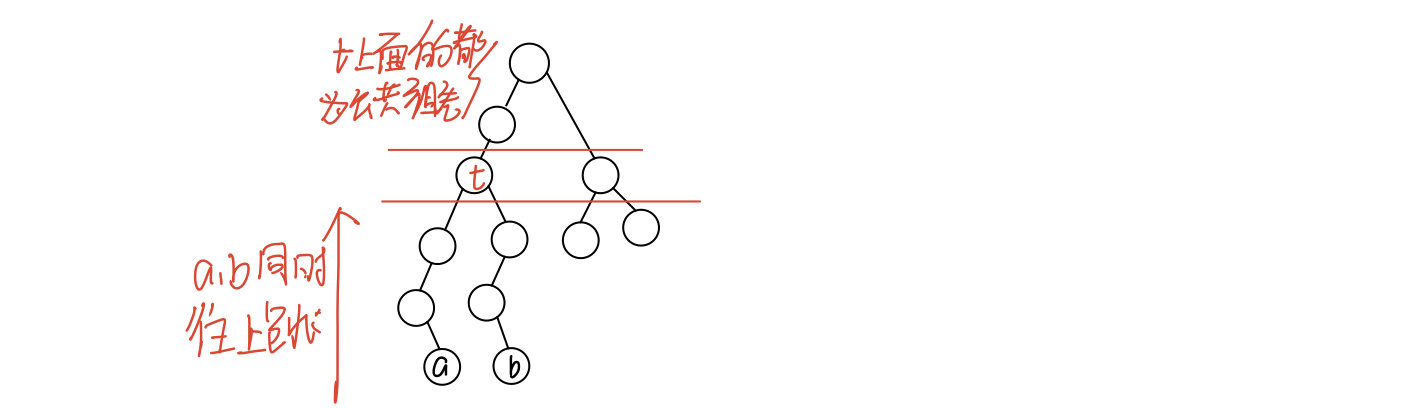
(3) $LCA$往上跳举例
假如$a$要跳到它上面$11$步的祖先的下一层,$11=1011$,那么就是依次往上跳$8$、$2$步,即从大往小跳,在枚举往上跳$8$步后枚举往上跳$4$步的时候就会出现跳到最近公共祖先的上面的公共祖先的问题,在$(2)$中有解释,我们会不执行向上跳$4$的操作,继续往上跳$2$步的操作,最后组合出跳到$a$上面$11$步的下一层的跳法,跳到该层结点
$(1)$ 往上跳的过程中是从大的步数往小的跳
① $depth[fa[a][k]] >= depth[b]$保证$a$往上跳到$b$的相同高度的时候不会跳到更高的地方,且会将所有组成a到b之间距离的二进制数全部跳了。
② $fa[a][k] != fa[b][k]$保证不会跳到最近公共祖先的面的点,且会将两个点到最近公共祖先的下一层之间的距离的二进制数全部跳了,保证只会跳到最近公共祖先的下一层
$(2)$ 预处理的时候是是从小的步数往大二的步数跳,即$k$从大枚举,且不能枚举到$0$($0$已经特殊处理),因为$f[j][k]$依赖于更小的$f[j][k-1]$先算出来
fa[j][0] = t;
for (int k = 1; k <= 16; k ++)
fa[j][k] = fa[fa[j][k - 1]][k - 1];
即把所有合法的跳完,一定在最近公共祖先的下一层
预处理出$fa[i][j]$时间复杂度$O(NlogN)$,查询的时间复杂度$O(logN)$,因此总的时间复杂度为$O(NlogN)$
$Example:$
模板题:$Acwing1172$.祖孙询问
利用$LCA$求两个点之间之间的最大边权和次大边权:$Acwing356$.次小生成树
利用$LCA$实现两点计数数中环上边被覆盖的次数:$Acwing352$.闇の連鎖
$3.tarjan$离线求$LCA$-$O(N+M)$
在深度优先遍历的时候将所有点分成$3$类:
① 已经遍历过的点,且回溯过的点-标记为$1$
② 正在搜索的分支上的点(在递归搜索栈中的点)-标记为$2$
③ 还未搜索过的点-标记为$0$
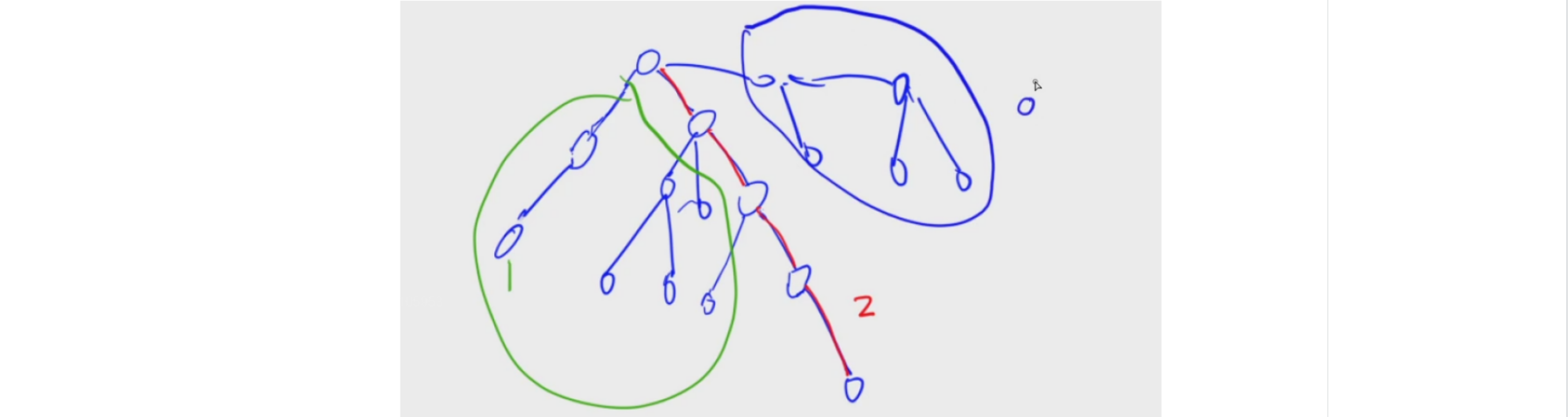
然后利用并查集,将所有标记为$1$的点都合并到它的父节点上面,然后每次搜索到标记为2的点的时候,就将符合另一个点标记为$1$的询问,最近公共祖先记录为标记为$1$的点合并到的父节点编号
求距离
利用最近公共祖先求两个点之间的距离,用$d[ ]$数组记录所有点到根节点之间的距离,设$x$、$y$的最近公共祖先为$p$,那么$x$和$y$之间的距离就为$d[x]+d[y]-2×d[p]$
$tarjan$逻辑
① 遍历到$u$这个点的时候先将这个点标记为1类点
② 访问$u$的所有子节点,同时回溯之后才能将子节点合并到$u$上
回溯前合并可能对子树中求最短距离造成影响,因为子树$j$中的点是都要合并到$j$上,如果回溯前合并就路径压缩到了$u$上
③ ②中已经将u的所有子节点都标记为2类点了,现在$u$为一类点,因此可以遍历所有询问,将满足询问$u$和已经确定的2类点之间的距离算出来
④ $u$的所有子节点回溯完过后要将$u$标记问2类点

