bellman-ford 算法

bellman算法可以检测负环
如果第n次循环更新了边，说明一条最短路上有n个点，也就是有n+1条边 根据抽屉原则 有两个点是同样的点
就形成了负环 
打个比方说 3个点 3条边 必定为环

但不是有负环的一定求不出最短路 参考上图
如果2的负环边不在1-n的最短路上，就没有影响

backup数组的作用

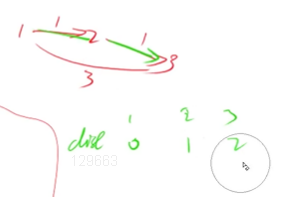
前提：k = 1 ，也就是只能用1条边来更新数组
第0次：dist[1] = 0 dist[2] = 正无穷 dist[3] = 正无穷
如果我们不备份，那么可能出现以下的状况：

更新语句:dist[b] = min(dist[b] , dist[a] + w);
第一次内层循环：
dist[2] = 1 
dist[3] = 2
重点：更新了两条边，在一次循环内(内层循环)

如果我们用备份来更新:
dist[b] = min(dist[b],backup[a] + w)
第0次：dist[1] = 0 dist[2] = 正无穷 dist[3] = 正无穷
第1次: dist[2] = backip[1] + w = 2 , dist[3] = backup[2] + w = 正无穷
也就不会被更新成2了

为什么要用0x3f3f3f3f / 2
看下图：

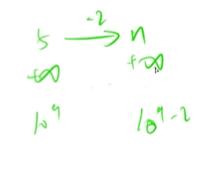
如果我们的判断最后dist[n] 是不是无解
之前用的语句是 if(dist[n] == 0x3f3f3f3f)
那么如果存在负权边 
dist[5] = 正无穷 5到n的距离是-2 那么就会把n的dist更新为正无穷-2 初始的判断条件就不能判断是否是无解了
m给定的范围为10000 k给定的范围是500 也就是最多会产生 0x3f3f3f3f - 5x10^6的值 
这个值是大于0x3f3f3f3f / 2的
所以我们把条件变为dist[n] < 0x3f3f3f3f / 2 作为dist[n] 有解