朴素版dijkstra算法

S:表示已经确定最短路的点

① dist[1] = 0 dist[1到其他点的距离] = 正无穷
② for v(点) 1 - n (迭代n次)
    找到t(不在s中，距离最短的点 也就是当前没有确定的点的最小值) 距离指的是1号点到当前这个点(t)的最短距离（迭代n次）
    把t加到s中
    用t更新其他点的距离（迭代n次）

总时间复杂度是O(n^2)

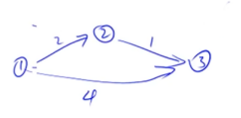
第一步: dist[1] = 0 , dist[2] = dist[3] = 正无穷
第二步: 找到不在s中，距离最近的点 也就是dist[1] （一号点）（加入s）
第三步：用一号点更新一下其他所有点到起点的距离 dist[2] = 2 dist[3] = 4 (2,3点还没被加到s中)
第四步：找到不在s中，距离最近的点 也就是dist[2] （二号点）（加入s）
第五步：用二号点更新一下其他所有点到起点的距离 dist[3]（原本） > dist[2] + 1（2->3的权值） dist[3] = 3
第六步：找到不在s中，距离最近的点 也就是dist[3] （三号点）（加入s）

堆优化版dijkstra算法

① dist[1] = 0 dist[1到其他点的距离] = 正无穷

② for v(点) 1 - n (迭代n次)
    找到t(不在s中，距离最短的点 也就是当前没有确定的点的最小值) 距离指的是1号点到当前这个点(t)的最短距离（用堆来存储 堆取最小值是O(1) 循环n个点 总复杂度是O(n)）
    把t加到s中 O(n)
    用t更新其他点的距离（堆修改一个点是logn 循环m次）也就是O(mlogn)