题目分析:
因为木块的摆放方式有两种,一种横着放,一种竖着放;
如果我们先横着摆放木块直到横着摆放已经不可以了,在将剩余的空格用竖着的木块进行填充,使得整个长方形容器没有空余的格子这就是我们想要的一种状态。
DP思路:
已经确定了木块横着摆放的所有方式就是题目的解。
DP数组为f[i][j],该集合划分的的意义是:
长方形容器中前列木块已经摆好不会再向前i列中进行填充了,第i列木块状态的十进制表示数为j。
集合的属性是种类的数量,集合的计算划分是重点,
对于集合的划分我们从最后一步开始看,
第i列时,我们看i-2列到i-1列的状态,首先第i列的状态j有2^n种,0000–>2^n - 1
这每一种我们不是都要,这时候我们要建立筛选条件,什么状态是我们需要保留的。
条件1:
因为我们是先摆放横着的木块,竖着的木块来填充,因为每一个木块的规格都是12的,那么在第i列每两个由第i-1列伸过来的木块之间的空余出来的空间格子数必须为偶数,如果是奇数,那么这种状态筛掉,因为奇数我们竖着填充进木块那么这个长方形容器一定有空余的格子,按照题意这是非法的
条件2:*
如果在某一行t,i-2列向i-1列伸出一个木块,但是第i列的j在改行的二进制状态值为1,那么这就会产生冲突,因此遇到这样的情况我们也应该吧该种j状态筛掉。
如图所示:
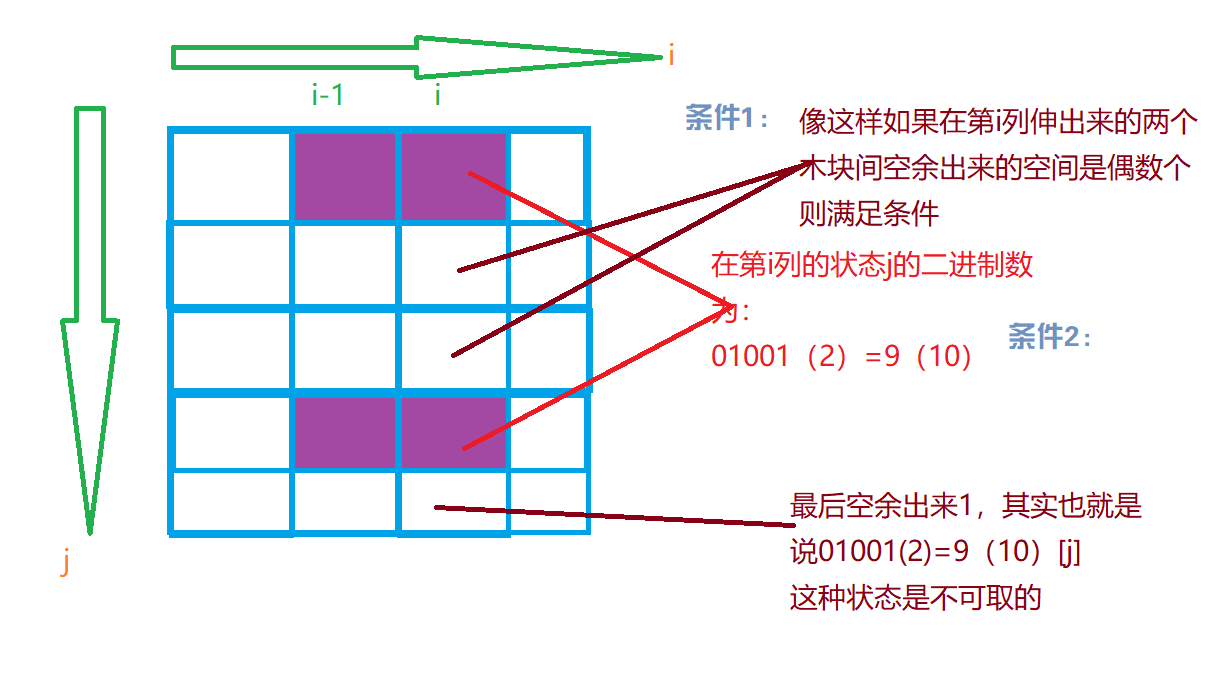
代码:
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=12,M=1<<12;
typedef long long ll;
ll f[N][M];
vector<vector<int>>cot(M);
bool st[M];
int main(){
int n,m;
while(cin>>n>>m,m||n){
//如果m&n==0则退出
//先进行条件1的判断,并存储合理的状态j
memset(st,0,sizeof st);
for(int i=0;i<(1<<n);i++){
int flag=1;
int cnt=0;
for(int j=0;j<n;j++){
if((i>>j)&1){
if(cnt&1){
//当前Dp列两个由上一列伸出的块之间的空格数量为奇数
flag=0;//当前状态i不可取
cnt=0;
break;
}
cnt=0;
}
else
cnt++;
}
//对最后一个伸出的块到最后一行的空格数量进行特判
if(cnt&1)
flag=0;
st[i]=flag;
}
//根据条件2对状态j进行筛选
for(int i=0;i<(1<<n);i++){
cot[i].clear();//!!!!!!!!!
for(int j=0;j<(1<<n);j++){
if(st[i|j]&&(i&j)==0){//!!!!!!!!!!!!!!
cot[i].push_back(j);
//对上一列的状态j进行遍历,如果与当前列的
//状态j不冲突就存入数组
}
}
}
//Dp过程
memset(f,0,sizeof f);
f[0][0]=1;
//由于当前列为第0列,前0列已经填充完毕,也就是第-1列
//当然0列的状态中没有二进制为1的位,因为第-1列其实
//并没有数字,也就是没有伸进来的木块,因此
//合法状态j=0;这样填充方式也就是1
for(int i=1;i<=m;i++){
for(int j=0;j<(1<<n);j++){
for(auto t:cot[j]){
f[i][j]+=f[i-1][t];
}
}
}
cout<<f[m][0]<<endl;
}
return 0;
}
解释:
!!!!!!!!代码中这样的符号是我写这道题目的时候学会了这道题目的思路后因为这两个地方而不能AC的点,
1. 为什么是12呢而不是11呢,因为是0~2^11这个范围一共有2^11+1个数,如果我们将数组的范围开到2^11,那么数组越界,其实也可以写成2^11+2这种

