2020江西省ACM省赛题解
A-Simple Math Problem
思路:分解质因数+容斥定理
对于$j\in[1,n]$,如果有$i\in[j,n]$并且$gcd(i,j)==1$,则$ans$加上$j$的数位和$f(j)$。我的做法是,对于每一个$j$求出有在$[j,n]$范围内有多少个数与它互质,然后加上$f(j)*cnt$就可以,问题转换成了经典问题:求出与$[l,r]$范围内与$x$互质数的个数,我们可以用前缀和的思想,先求出$[1,r]$与x互质数的个数,之后减去$[1,l-1]就行$。
定理1:$[1,n]$中,x的倍数有$\lfloor n/x\rfloor$个
定理2:两个数互质,则质因子互不相同。两个数不互质,至少存在一个质因子相同
定理3:若$n$能被$x,y$整除,并且$x$和$y$是质数,则$n$一定也能被$x*y$整除。当$x,y$不是质数的时候不满足
求互质的个数不好求,就求出不互质的个数,即两个数有相同的质因子的时候,我们对x进行分解质因数,若不互质,$x$的质因数必定能够整除与$x$不互质的数,个数就是$\lfloor n/质因数\rfloor$,这样会有重复,所以需要用到容斥定理处理一下。
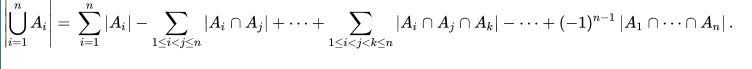
代码
#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long LL;
typedef pair<int,int>PII;
const int N=1e6;
int get(int x)
{
int sum=0;
while(x)
{
sum+=x%10;
x/=10;
}
return sum;
}
LL solve(int x,int n)
{
vector<int>v;
for(int i=2;i<=x/i;i++)//分解质因数
{
if(x%i==0)
{
v.push_back(i);
while(x%i==0)
{
x/=i;
}
}
}
if(x>1) v.push_back(x);
int cnt=v.size();
LL cnt1=0;
for(int i=1;i<1<<cnt;i++)//枚举每一种情况
{
LL p=1,s=0;
bool flag=true;
for(int j=0;j<cnt;j++)
{
if(i>>j&1)
{
if(p*v[j]>n)
{
flag=false;
break;
}
p*=v[j];
s++;
}
}
if(flag)//容斥定理
{
if(s&1) cnt1+=n/p;
else cnt1-=n/p;
}
}
return n-cnt1;
}
int main()
{
int n;
cin>>n;
LL ans=0;
for(int i=1;i<=n;i++)
{
ans+=get(i)*(solve(i,n)-solve(i,i-1));
}
cout<<ans;
return 0;
}
B-Apple
思路:思维
第一个人分1个,第2个人分两个,最后一个人分n个是合法的最优策略,如果苹果数$n>=sum$就合法,否则不合法。
代码
#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long LL;
typedef pair<int,int>PII;
const int N=1e6;
int main()
{
int T;
cin>>T;
while(T--)
{
LL n,m;
cin>>n>>m;
LL sum=(m)*(1+m)/2;
if(sum<=n) cout<<"possible"<<endl;
else cout<<"impossible"<<endl;
}
return 0;
}
C-Charging
思路:二分
我不会
D-Chinese Valentine’s Day
思路:SA
我不会
E-Color Sequence
思路:状压+异或前缀和
如果$sum[i]$为数组$a$的前$i$项的异或和,则$a$数组$l$到$r$的异或和就等于$sum[r] \bigoplus sum[l-1]$
那么对于一段$[1,r]$来说,异或前缀和为$b[r]$,那么如果想要以$r$结尾的异或为0的子段的右半部分,那么只需要前面出现过一个数$b[i] == b[r]$,那么$[i + 1,r]$这一段异或和为0,就是:如果在$r$的前面出现一个i,使得$b[i]==b[r]$则$i+1$到$r$的异或和为0。
有了这些前置知识,这题只要状态压缩一下就行。用一串二进制表示颜色是奇数还是偶数,偶数置0,奇数置1,20种颜色,最多$2^{20}$个状态。
代码^
#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long LL;
typedef pair<int,int>PII;
const int N=1e6+10;
int a[N],cnt[1<<21];
LL ans;
int main()
{
CLOSE;
int n;
cin>>n;
cnt[0]=1;
for(int i=1;i<=n;i++)
{
int x;
cin>>x;
a[i]=a[i-1]^(1<<x);//状态压缩
ans+=cnt[a[i]];
cnt[a[i]]++;
}
cout<<ans;
return 0;
}
F-Magical Number
思路
DFS,不会。。
G-Mathematical Practice
思路:推公式+快速幂
一个集合有n个元素,则有$2^n$个子集,然后推出来一个二项式展开式,最后就是$(m+1)^n$
代码
#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long LL;
typedef pair<int,int>PII;
const int N=1e6;
LL qpow(LL a,LL b,LL p)
{
LL ans=1;
while(b)
{
if(b&1) ans=ans*a%p;
b>>=1;
a=a*a%p;//这里别忘了mod
}
return ans;
}
int main()
{
LL n,m;
cin>>n>>m;
cout<<qpow(m+1,n,998244353);
return 0;
}
H-Sequence
思路:线段树+二分
线段树维护区间最小值,然后二分查找$x$位置往左能走到的极限位置$l$,往右能走到的极限位置$r$,答案就是$(x-l+1)*(r-x+1)$
代码
#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define ul u<<1
#define ur u<<1|1
using namespace std;
typedef long long LL;
typedef pair<int,int>PII;
const int N=1e5+10;
struct node{
int l,r,v;
}t[4*N];
int a[N];
void pushup(int u)
{
t[u].v=min(t[ul].v,t[ur].v);
}
void build(int u,int l,int r)
{
t[u].l=l,t[u].r=r;
if(l==r)
{
t[u].v=a[l];
}
else
{
int mid=(l+r)>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
pushup(u);
}
}
void modify(int u,int x,int c)
{
if(t[u].l==t[u].r&&t[u].l==x)
{
t[u].v=c;
}
else
{
int mid=(t[u].l+t[u].r)>>1;
if(x<=mid) modify(ul,x,c);
else modify(ur,x,c);
pushup(u);
}
}
int query(int u,int l,int r)
{
if(l<=t[u].l&&t[u].r<=r)
{
return t[u].v;
}
else
{
int mid=(t[u].l+t[u].r)>>1;
int ans=0x3f3f3f3f;
if(l<=mid) ans=min(ans, query(ul,l,r));
if(r>mid) ans=min(ans,query(ur,l,r));
return ans;
}
}
int main()
{
CLOSE;
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
while(m--)
{
int op;
cin>>op;
if(op==1)
{
int x,y;
cin>>x>>y;
modify(1,x,y);
}
else
{
int x;
cin>>x;
int minn=query(1,x,x);
int ll,rr;
int l=1,r=x;
while(l<r)
{
int mid=(l+r)>>1;
if(query(1,mid,x)>=minn) r=mid;
else l=mid+1;
}
ll=l;
l=x,r=n;
while(l<r)
{
int mid=(l+r+1)>>1;
if(query(1,x,mid)>=minn) l=mid;
else r=mid-1;
}
rr=l;
cout<<1ll*(x-ll+1)*(rr-x+1)<<"\n";
}
}
return 0;
}
I-Simple Math Problem
思路:等差数列求和
推公式就行
#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long LL;
typedef pair<int,int>PII;
const int N=1e6;
int main()
{
LL n,x,y;
cin>>n>>y>>x;
y=-y;
LL k=abs(y-x);
if(k<=n-1)
{
cout<<k*(k+1)/2+k-x<<endl;
}
else
{
LL sum=(1+n)*n/2;
LL cnt=(k-n);
LL temp=cnt*(n-1)-cnt*(cnt-1)/2+n-x-1;
cout<<sum+temp<<endl;
}
return 0;
}
J-Split Game
思路:SG函数
不会
K-Travel Expense
思路:floyd+二分答案
天数就是距离,用floyd跑出,直接二分答案就行
代码
#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long LL;
typedef pair<int,int>PII;
const int N=105;
int a[N][N];
bool check(LL x,int d,LL w)
{
LL sum=0;
LL t = x;
for(int i=1;i<=d;i++)
{
sum+=x;
x*=t;
if(sum>w) return false;
}
return true;
}
int main()
{
CLOSE;
int n,m;
cin>>n>>m;
memset(a,0x3f,sizeof a);
for(int i=1;i<=n;i++) a[i][i]=0;
for(int i=1;i<=m;i++)
{
int x,y;
cin>>x>>y;
a[x][y]=a[y][x]=1;
}
for(int k=1;k<=n;k++)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
}
}
}
int T;
cin>>T;
while(T--)
{
int x,y;
LL w;
cin>>x>>y>>w;
int d=a[x][y];
LL l=0,r=1e9+10;
while(l<r)
{
LL mid=(l+r+1)>>1;
if(check(mid,d,w)) l=mid;
else r=mid-1;
}
cout<<l<<endl;
}
return 0;
}
L-WZB’s Harem
思路:状态压缩+记忆化搜索
记忆化搜索就是dp,复杂度是一样的。要注意记忆化搜索的时候必须返回值,不是普通的dfs。这题每行摆放皇后的时候与前面所有行的状态有关系,所有需要状压一下,最后别忘了乘上一个排列数。
代码
#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long LL;
typedef pair<int,int>PII;
const int mod=1e9+7;
int a[21][21],n;
int f[21][1<<20];
int dfs(int x,int state)
{
if(x==n+1) return 1;
if(~f[x][state]) return f[x][state];
LL sum=0;
for(int i=1;i<=n;i++)
{
if(a[x][i]==1||state>>(i-1)&1) continue;
sum=(sum+dfs(x+1,state|1<<(i-1)))%mod;
}
f[x][state]=sum;
return sum;
}
int main()
{
CLOSE;
cin>>n;
memset(f,-1,sizeof f);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cin>>a[i][j];
}
}
LL x=1;
for(int i=1;i<=n;i++) x=x*i%mod;
cout<<x*dfs(1,0)%mod;
return 0;
}
M-Zoos’s Animal Codes
思路:输出答案
签到题
代码
#include <bits/stdc++.h>
#define CLOSE ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long LL;
typedef pair<int,int>PII;
const int N=1e6;
int main()
{
string a,b;
cin>>a>>b;
cout<<a<<b;
return 0;
}

