拆点思考方式和应用场景

正常当我们求最短路，或者是最短路相关的问题时，我们往往认为，图中的一个点就是实实在在存在的一个点。但是实际上，对于问题中的一个点，我们之所以只把它当作”一个点”，是因为它只存在一种我们需要的状态，即最短路长度，我们仅仅需要一个dist数组即可表示。但是实际上，我们图中的点，往往不止一种可能的状态。举几个例子:

• 拯救大兵瑞恩

拯救大兵瑞恩这一题中，我们如果把每个(x, y) 当作一个实际存在的点(具象)，我们发现是不够的。因为一个点具有很多状态。此时我们不妨把每个点假想成多个状态点，让它们平等地存在于图中，联系这些点的东西就是点的编号(坐标)。

• 观光这一题中， 我们需要求最短路径的同时，需要求次短路径。实际上，统计路径的条数只是附带的。在这种情况下，我们每个点相当于具有两种不同状态，在图中以两种形态存在: 1. 经过这点的最短路径 2. 经过这点的次短路径。所以此时我们可以将点拆开，每个点具有两种状态，分别存储最短路径的长度和次短路径的长度。我们可以论证:

• 存储最短路径的点一定具有正确性。因为如果不考虑次短路，就是简单的单状态下的最短路。

• 存储次短路径的点需要有以下考虑:
  1. 每个点的最短路径绝对不会被前驱的次短路径更新。反证法可以论证。
  2. 每个点的次短路径可以由前驱的次短路径、最短路径、自身的当前最短路径更新。(因为算法过程中直至出队前最短路径都没有确定，次短路径也就因此没有确定)
  3. 每个点(包含最短路径状态点和次短路径状态点)，在出队时，距离都确认了，并且不会再有所更改。
• 每一个点(具象的点)都被分到了两个不同的层次，因为具象的点之间我们连了边，我们可以认为拆分后如下图:

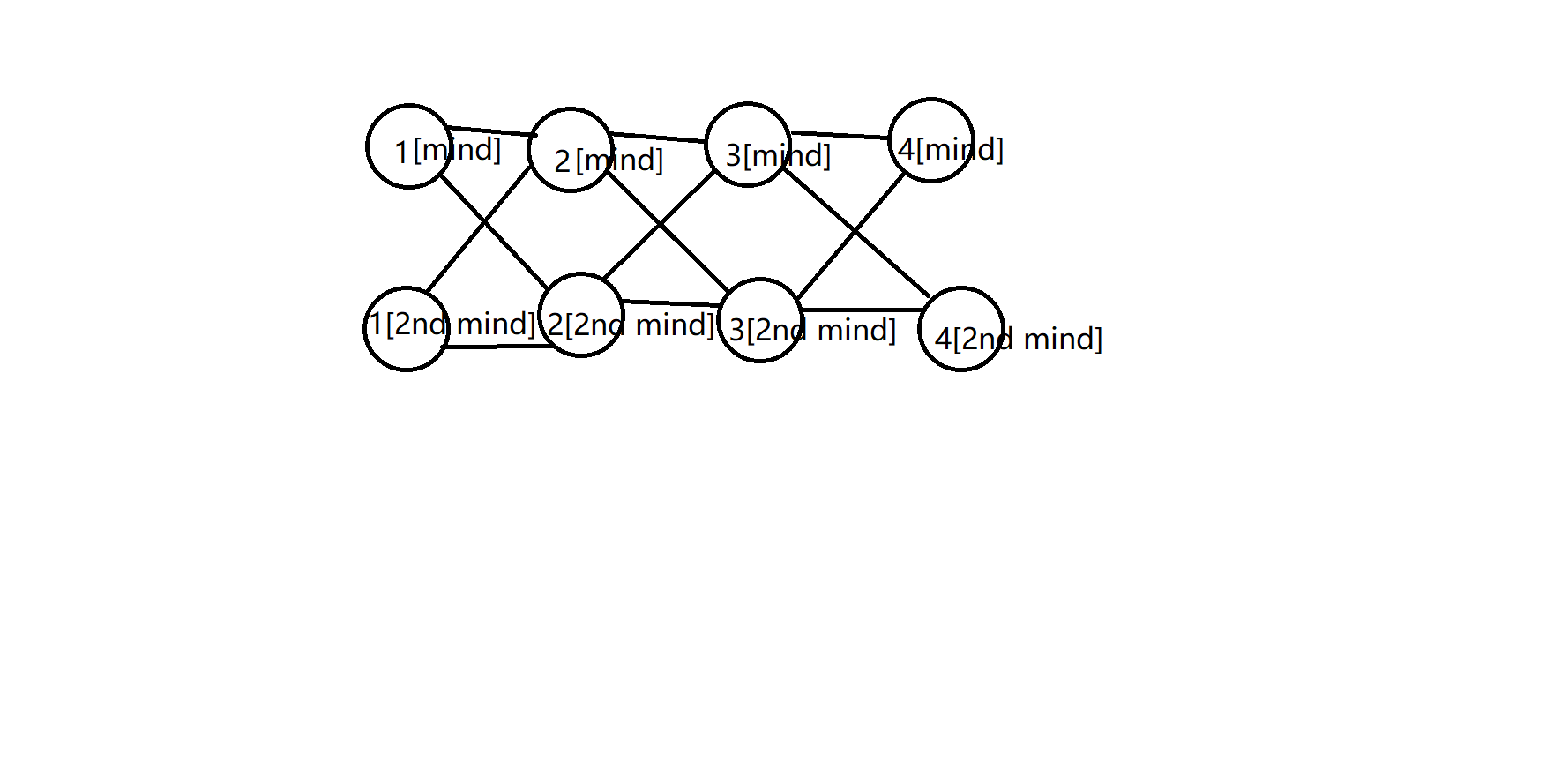
总而言之: 图中的点应该是抽象的状态点，而不是图像上具象的点。