流网络 是由一些点和有向边组成的可以有环的图。记作：$G = (V, E)$ ( $V$ 表示点集，$E$ 表示边集 )。流网络中有两个特殊的点，源点 和 汇点。

流网络 里的每一条边都有一个属性，记录该边的 容量（该边每秒最多能流过的单位流量），一般用 $c$ 表示。

源点 拥有源源不断的流量可以流出去。汇点 可以容纳无穷多的流量。

注意： 我们在讨论流网络时为了简化讨论，默认不存在反向边，因为就算存在反向边，我们也可以将反向边中间加上一个点，这样就从两个点之间的双向边变成了三个点之间的环。并且如果有一条边不存在，我们就定义它的容量为 $0$。

如下图，为一个流网络，有一个源点和一个汇点，每条边上都有对应的容量。

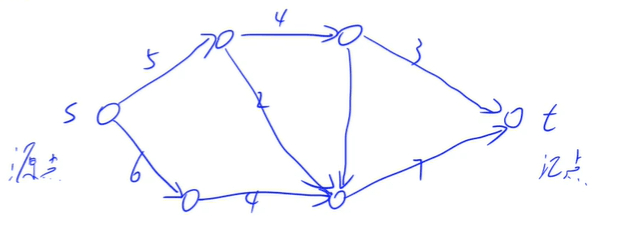
可行流： 对于任意满足以下两个条件的流，被称为 可行流，记作：$f$。

1. 容量限制，$0 \leq f(u, v) \leq c(u, v)$
2. 流量守恒，$\forall x \in V / \lbrace s, t \rbrace，\sum_{(v, x) \in E}f(v, x) = \sum_{(x, v) \in E}f(x, v)$

注意： 到此为止都不需要考虑反向边。

可行流的流量值： 我们将每秒从源点流出的流量（每秒流入汇点的流量）作为可行流的流量值，记作：$\vert f \vert = \sum_{(s, v) \in E} f(s, v) - \sum_{(v, s) \in E} f(v, s)$

如下图，为上文中的流网络对应的一个可行流，每条边的红字容量为该边在可行流中的容量。

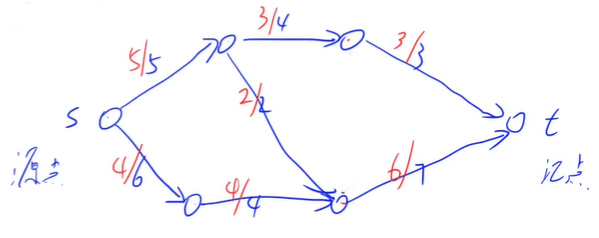
最大流： 流网络中流量值最大的一个 可行流 被称为该流网络的 最大流，因此又称为 最大可行流。

残量网络： 对于任意一个流网络 $G$ 中的任意一个可行流 $f$，都能对应一个残量网络，记作 $G_f$。

对于定义一个可行流的残量网络，$V_f = V, E_f = E$ 和 $E$ 中的所有反向边。当 $(u, b) \in E$ 时，$c’(u, v) = c(u, v) - f(u, v)$。当 $(v, u) \in E$ 时，$c’(u, v) = f(v, u)$

如下图，为上文中的可行流对应的残量网络，蓝边为正向边，红边为反向边，每条边上都有对应的容量。

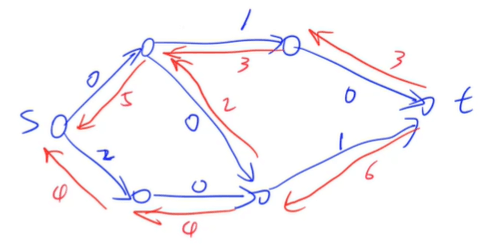
割： 对于流网络 $G = (V, E)$，将点集$V$ 分成两个子集 $S, T$（子集中的节点不需要连通），保证 $S \cup T = V, S \cap T = \emptyset $，且 $s \in S, t \in T$，像这样的一种将点集划分的结果，就称为 割。

割的容量： 所有从 $S$ 指向 $T$ 的边的容量之和，即 $c(S, T) = \sum_{u \in S} \sum_{v \in T} c(u, v)$。

最小割： 从流网络中割的所有划分方案中找出割的容量的最小值，被称为该流网络的最小割，又叫最小割的容量。$n$ 个节点的流网络中存在 $2^{n-2}$ 种割的划分方案。

割的流量： 流网络中所有从 $S$ 流到 $T$ 的流量，减去所有从 $T$ 流到 $S$ 的流量，即 $f(S, T) = \sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{u \in T} \sum_{v \in S} f(u, v)$

性质 $1$： 对于 $\forall [S, T], \forall f$ 都有 $f(S, T) \leq c(S, T)$

证明 $1$： 因为 $f(S, T) = \sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{u \in T} \sum_{v \in S} f(u, v)$，且 $\sum_{u \in T} \sum_{v \in S} f(u, v) >= 0$，所以 $f(S, T) \leq \sum_{u \in S} \sum_{v \in T} f(u, v) \leq \sum_{u \in S} \sum_{v \in T} c(u, v) = c(S, T)$，由此得出 $f(S, T) \leq c(S, T)$

性质 $2$： 对于 $\forall [S, T], \forall f$ 都有 $f(S, T) = \vert f \vert$

证明 $2$： 因为 $f(S, V) = f(S, S) + f(S, T)$，而 $f(S, S) = 0$，所以 $f(S, T) = f(S, V) = f(\lbrace s \rbrace, V) + f(S - \lbrace s \rbrace, V)$，而 $f(S - \lbrace s \rbrace, V)$ 中 $S - \lbrace s \rbrace$ 不包含 $t$ 也不包含 $s$，由于 $f(S - \lbrace s \rbrace, V)$ = 出去的流量 - 回来的流量，在不包含源点和汇点的前提下，其他点的流量的流出和流入都是固定的，流出多少就流回来多少，所以 $f(S - \lbrace s \rbrace, V) = 0$。因此 $f(S, T) = f(\lbrace s \rbrace, V) = \vert f \vert$。

性质 $3$： $f(X, Y) = -f(Y, X)$。

证明 $3$： $f(X, Y) = \sum_{u \in X} \sum_{v \in Y} f(u, v) - \sum_{u \in X} \sum_{v \in Y} f(v, u) = - (\sum_{u \in X} \sum_{v \in Y} f(v, u) - \sum_{u \in X} \sum_{v \in Y} f(u, v)) = -f(Y, X)$

性质 $4$： $f(Z, X \cup Y) = f(Z, X) + f(Z, Y)$

证明 $4$： $f(Z, X \cup Y) = (\sum_{u \in Z} \sum_{v \in X} f(u, v) + \sum_{u \in Z} \sum_{v \in Y} f(u, v)) - (\sum_{u \in Z} \sum_{v \in X} f(v, u) + \sum_{u \in Z} \sum_{v \in Y} f(v, u)) = f(Z, X) + f(Z, Y)$

性质 $5$： $f(X, X) = 0$

证明 $5$： $f(X, X) = \sum_{u \in X} \sum_{v \in X} f(u, v) - \sum_{u \in X} \sum_{v \in X} f(v, u) = 0$

推论： 通过 性质 $1$ 和 性质 $2$ 可知，对于 $\forall [S, T], \forall f$，都有 $\vert f \vert \leq c(S, T)$，所以就有 最大流 $\leq$ 最小割（对于证明 最大流最小割定理 有重要作用）

最大流最小割定理

对于任意一个流网络 $G = (V, E)$ 都满足：

$(1)$ 可行流 $f$ 是最大流 $<=>$ $(2)$ 可行流 $f$ 的残量网络中不存在增广路径 $<=>$ $(3)$ 存在某个割 $[S, T], \vert f \vert = c(S, T)$

证明：

$(1) => (2)$，反证法，假设 $f$ 是最大流，且 $G_f$ 中存在增广路径，意味着 $G_f$ 中存在一个流量 $> 0$ 的可行流 $f’$，那么就可以发现 $f + f’$ 同样是原网络的一个可行流，并且由于 $\vert f’ \vert > 0$，所以 $\vert f + f’ \vert > \vert f \vert$，说明 $f$ 不是原网络的最大流，与假设矛盾，证毕。

$(2) => (3)$，我们只需要构造一个割，使得它在残量网络中不存在增广路径，且 $\vert f \vert = c(S, T)$。定义集合 $S$ 为在 $G_f$ 中从 $s$ 出发沿着容量 $> 0$ 的边走，能走到的所有的点。因为残量网络中不存在增广路径，所以集合 $S$ 中不可能包含 $t$，再定义集合 $T = V - S$。这就是借助残量网络在原网络中构造的一个合法的割。对于点 $x \in S, y \in T$ 连成的正向边 $xy$，由于 $x$ 和 $y$ 在残量网络中不相通，所以 $f’(x, y) = 0$，即 $c(x, y) - f(x, y) = 0$，得出 $f(x, y) = c(x, y)$。对于点 $a \in T, b \in S$ 连成的反向边 $ab$，由于残量网络中不无法从 $b$ 走到 $a$，因此得出 $c’(b, a) = 0$，即 $f(a, b) = 0$。这样就可以发现，在原网络中所有从 $S$ 走向 $T$ 的边的流量 $=$ 容量，所有从 $T$ 走向 $S$ 的边的流量 $= 0$，因此 $\vert f \vert = f(S, T) = \sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{u \in S} \sum_{v \in T} f(v, u) = \sum_{u \in S} \sum_{v \in T} f(u, v) = \sum_{u \in S} \sum_{v \in T} c(u, v) = c(S, T)$，证明如果残量网络中不存在增广路径，则一定存在某个割 $[S, T]$，使得 $\vert f \vert = c(S, T)$

$(3) => (1)$，由上文最小割的推论中已知 $\vert f \vert \leq c(S, T)$，且最大流是可行流的一种，所以最大流 $\leq c(S, T)$。由于最大流是最大的可行流，可得 $\vert f \vert \leq$ 最大流，而 $\vert f \vert = c(S, T) \geq$ 最大流，即 $\vert f \vert \geq$ 最大流。综上得出 $\vert f \vert = $ 最大流。并且！已证最大流 $\leq$ 最小割，而最小割又是割的容量的最小值，得出最小割 $\leq c(S, T) = \vert f \vert \leq $ 最大流，即最小割 $\leq$ 最大流，最终得出最大流 $=$ 最小割。

原网络 $G$ 的可行流 $f$ 和残量网络 $G_f$ 的可行流 $f’$ 的关系

$f + f’$ 也是 $G$ 的一个可行流。

$\vert f + f’ \vert = \vert f \vert + \vert f’ \vert$

证明：

首先定义一下两个可行流的相加。如果是两个同向边相加，则将容量累加，如果是反向边，就把残量网络里的流量在原网络里减去。

然后看可行流需要满足的两个条件。

首先看是否满足容量限制。对于同向边，由于 $0 \leq f’(u, v) \leq c’(u, v) = c(u, v) - f(u, v)$，因此同向边是满足 $0 \leq f’(u, v) + f(u, v) \leq c(u, v)$ 的。

对于反向边，由于 $0 \leq f’(u, v) \leq c’(u, v) = f(v, u) \leq c(v, u)$，因此反向边是满足 $0 \leq f(v, u) - f’(u, v) \leq c(v, u)$ 的。

综上可知，两个可行流相加是满足容量限制的。

对于是否满足流量守恒，这不需要证明，由于原网络满足流量守恒，残量网络也满足流量守恒，那么对于同向边，流入的累加流入的，流出的累加流出的，满足流量守恒，而反向边只不过是相互抵消了一部分的流量，同样满足流量守恒。

由此得出，原网络的任意一个可行流加上残量网络的任意一个可行流所得到的流都是原网络的一个可行流。

对于计算得到的新流的流量值，因为流量值是可行流净往外流出的流量，因此新流的净往外流出的流量 = 原网络的可行流净往外流出的流量 + 残量网络的可行流净往外流出的流量

作用：

通过以上特性，任何一个在残量网络里面发现的流量 $> 0$ 的可行流，都能用来增加原网络的可行流。

同时得到一个推论，如果残量网络中存在任何一个流量 $> 0$ 的可行流，那么原网络里的可行流就一定不是最大的可行流。

对于最大流来说反过来也是正确的，即如果残量网络中不存在任何一个流量 $> 0$ 的可行流，那么原网络里的可行流就一定是最大的可行流。这个反命题可以通过上文的 最大流最小割定理 得出。

增广路径： 在残量网络中从源点出发，沿着容量 $> 0$ 的边，存在一条路径能走到汇点，这条路径被称为 增广路径。

注意： 增广路径一般指没有环的简单路径。

费用： 对于任意一个可行流 $f$，每条边 $(u, v)$ 都有流量 $f(u, v)$ 和 费用 $w(u, v)$，该可行流的费用为 $\sum f(u, v) \cdot w(u, v)$

最大费用流： 所有最大可行流中费用最大的流称为最大费用最大流

最小费用流： 所有最大可行流中费用最小的流称为最小费用最大流

注意： 一张图 $G$ 有最大流，那么就一定有最小费用最大流，但是存在一些特殊的图，图中存在一个从源点无法到达的闭环，闭环中的费用是负的，这时最小费用流可能比我们求出来的更小，因此我们求费用流的做法存在局限性，并不一定能求出最小费用最大流。

如何求最小费用最大流：

最小费用最大流是基于 EK 算法来求的，只需要把 EK 算法中找增广路径的 bfs 算法换成找最短路的 spfa 算法就可以求最小费用最大流了。

证明过程比较简单，假设当前的可行流 $f_1$ 在这个流量的前提之下费用是最小的，然后我们通过 spfa 又找到一个新的可行流 $f_2$，原可行流加上新可行流等于可行流 $f$。这里用反证法，假设 $f$ 不是费用最小的，$f_1$ 是当前费用最小的，$f_2$ 在 $f_1$ 的残量网络中是最短路，假设现在有一个可行流 $f’$，$f’$ 和 $f$ 的流量相等，但是费用更小，且 $f_2’ = f’ - f_1$，即 $f’ = f_1 + f_2’$，由于 $f’$ 和 $f$ 的流量相等，因此 $f_2’$ 和 $f_2$ 的流量也应该相等。而任何一条增广路径的费用都等于这条路径上的流量乘上路径长度，由于 $f_2$ 和 $f_2’$ 流量相等，且 $f_2’$ 的费用小于 $f_2$ 的费用，即 $f_2’$ 的路径长度比 $f_2$ 更短，说明找到了一条比 $f_2$ 更短的一条路径，和已有条件矛盾，反证得出 $f$ 是费用最小的，因此只要每次都沿着最短路来增广，最终得到的最大流的费用就一定是最小费用。

之前我们定义残量网络中反向边的流量等于正向边的容量，表示一个退流的概念，因此我们还需要定义一下反向边的费用，我们希望在退流的同时将费用也退掉，因此可以定义反向边的费用等于负的正向边的费用。

注意： 由于 spfa 算法遇到负权回路会进入死循环，所以我们常规的求最小费用最大流的算法并不能处理有负权回路的网络。如果网络中存在负权回路，就需要用消圈法来做。