$\Huge\color{BlueViolet}{大家好！今天我来讲一讲图的遍历}$

一，简介

图的遍历主要就是深度和广度优先遍历。下面引入一个图：

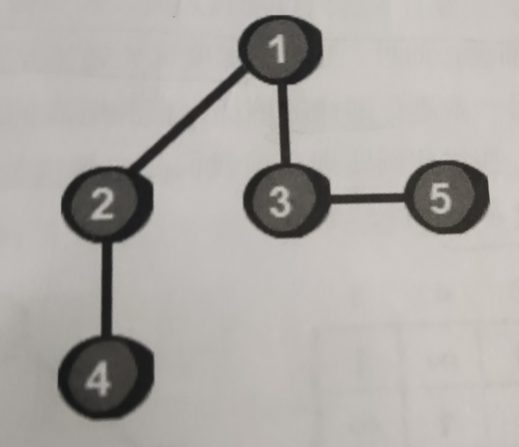
其实不难发现这个图是有两个部分组成，分别是每一个节点以及节点之间的连接。现在要遍历这个图其实就是按照编号来进行遍历，把这个图的每一个顶点遍历一遍。每一个顶点是第几个被访问到的叫做时间戳。下面是这个遍历的过程：

首先从1出发，发现2号顶点还没有走过1于是现在到了2号顶点，从2号顶点在开始，发现四号顶点没有走过，所以现在就走到四号顶点，在四号顶点发现没有没有走过的顶点了，所以现在要返回到2，在2发现还是老样子，没有可以去的地方，所以现在就再返回1，在1这个位置发现3没有走过，所以现在到了3这个位置，再从3到5.现在所有的顶点全部都走完了！！

二，图的储存

关于图的储存这里介绍一种简单的方法：邻接矩阵存储法，这个方法说白了就是用二维数组来储存这个图。看下图：

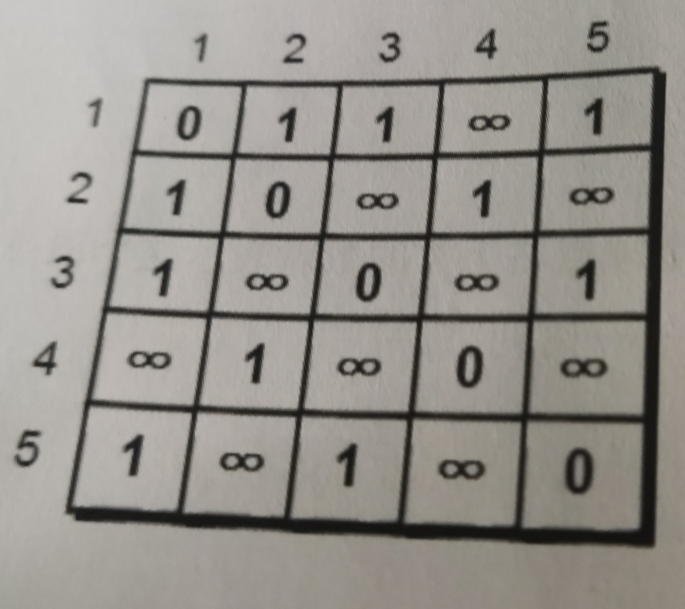
下面就来解释一下这个图吧：第一行也就是代表着第一个节点：对于第一个节点所相连的节点标记为1，看第一行，也就是1号节点和2，3，5有相连，主对角线是0是因为一个节点不能和它本身相连，没有相连的就是无穷，但是这个无穷不好表示所以就暂时用99999999来表示吧。这里还有一个细节，图分为2个类，有向图和无向图。其实从这个图里可以发现无向图矩阵是对称阵。但是如果是有向图的话，就只有在主对角线一边有路。

三，代码实现

#include <stdio.h>
int book[101] = { 0 };
int e[101][101];
int sum = 0, n;
void dfs(int cur) {//cur就是当前的编号
    int i;
    printf("%d", cur);
    if (sum == n) {//所有顶点已经访问了，所以就退出这个递归，在深度优先算法中这个退出条件非常重要
        return;//这个退出条件真的要认真思考，但是注意一下，其实这个退出条件是可以不止一个的
    }
    for (int i = 1; i <= n; i++) {//从一号到n号依次尝试，看每一个顶点是否有边相连。
        if (e[cur][i] == 1 && book[101] == 0) {//cur就是现在遍历到的节点，首先判断这个点是不是有路，接着再看这里有没有走过
            book[i] = 1;//book用来记录图是否已经遍历完了
            dfs(i);//从顶点i再开始出发             //这里其实还有一点，这种只有遍历，不是找相应的最短路径，所以没必要在函数返回的时候取消标记。                                           
        }
    }
    return;
}
int main() {
    int i, j, a, m, b;
    scanf_s("%d %d", &n, &m);
    for ( i = 1; i <= n; i++) {
        for ( j = 1; i <= m; j++) {
            if (i == j) {          //这里的意思就是对角线上的元素是0
                e[i][j] = 0;
            }
            else {
                e[i][j] = 9999;
            }
        }
    }
    //继续读入顶点的边
    for ( i = 1; i <= m; i++) {
        scanf_s("%d %d", &a, &b);
        e[a][b] = 1;
        e[b][a] = 1;//这个图是无向图,所以这个是双向的，如果是有向图就只要定义一个位置就好了
    }
    book[1] = 1;//记住第一个位置要先标记上
    dfs(1);//这里其实就是搜索的其实位置
    return 0;

这里就是有深度优先搜索来进行搜索（这里不说太多），这里补充解释一下深度优先搜索的核心代码吧：

//后面其实就是深度优先搜索的核心代码
void dfs(int step) {
    //判断边界,这里非常重要，在后续我觉得可以出一个博客专门举例子写这种边界
    //尝试每一种可能
    for (int i = 1; i <= n; i++) {
        //继续下一步
        dfs(step + 1);
        //后续操作其实在我的理解上就是递归树的返回，例如把标记取消，这个在最短路径这还是很重要的。
    }
    //返回
}

后面是广度优先搜索：

//广度优先搜索要用到队列的知识这里对队列知识还是做一个比较详细的介绍吧#include <stdio.h>
int main() {
    int i, j, n, m, a, b, cur, book[101] = { 0 }, e[101][101];
    int que[10001], head, tail;
    scanf_s("%d %d", &m, &n);
    for (i = 1; i <= n; i++) {
        for (j = 1; j <= n; j++) {
            if (i == j) {
                e[i][j] = 0;
            }
            else {
                e[i][j] = 999999999;
            }
        }
    }
    //读入顶点之间的边
    for (i = 1; i <= m; i++) {
        scanf_s("%d %d", &a, &b);
        e[a][b] = 1;
        e[b][a] = 1;
    }
    //后面开始广度搜索，现在其实也是做一个复习把
    head = 1;//这里是队列初始化
    tail = 1;
    //从一号顶点出发，说明一号顶点已经访问了
    que[tail] = 1;//这里就是把第一个节点入队。
    tail++;
    book[1] = 1;
    //后面还是老样子当队列不为空的时候来进行循环
    while (head < tail && tail <= n) {//head<tail在我的理解下好像就是队列的一个循环调节但两个相等的时候循环结束。tail<n是因为tail不能超过一行的限制
        cur = que[head];//从当前的编号开始向外拓展,首先要把这个当前编号放在头的位置
        for (i = 1; i <= n; i++) {
            //判断从顶点cur到i是否有边，并判断顶点i是否已经访问过了
            if (e[cur][i] == 1 && book[i] == 0) {
                book[i] = 1;
                //现在把上一个图相连的这个点入队
                que[tail] = i;
                tail++;
            }
            if (tail > n) {

                break;//第一行结束这个循环就break掉
            }
        }
        head++;//注意现在这个head就轮到下一个图了，比如2，也就是说现在已经到了第二行了，这个head非常重要甚至是队列遍历进行的条件。
    }
    for (i = 1; i < tail; i++)
        printf("%d", que[i]);
    return 0;
}（这些代码中的注释大多是自己的理解，可能有些错误）

这里后面再补充几个图来帮助大家理解吧。

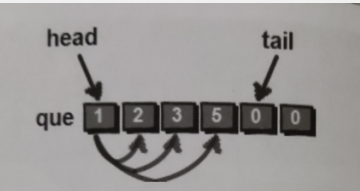
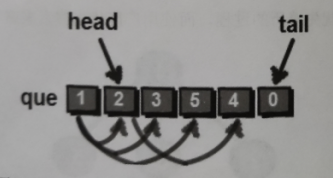
$\Huge\color{RoyalBlue}{其实这里队列还是简单的}$
$\Huge\color{RoyalBlue}{所以也没有用到结构来进行定义结构数组}$
$\Huge\color{RoyalBlue}{有的时候就要用到一个甚至多个结构数组了}$

$\Huge\color{RoyalBlue}{图的遍历其实只是一个基础}$
$\Huge\color{RoyalBlue}{本来想先想写深度优先搜索和广度优先搜索的}$

$\Huge\color{RoyalBlue}{但是想写的太多了，正好最近在看最短路径的问题}$
$\Huge\color{RoyalBlue}{所以就先写了比较基础的图的遍历，一步步来吧，加油}$

$\Huge\color{DarkTurquoise}{参考书籍 《啊哈！算法》}$
《啊哈！算法》百度百科