分析

很容易可以得到贪心策略：从叶结点开始往上搜索，如果某个节点往下的最大距离已经大于$d$，那么如果不删掉这个点，那么继续往上就需要删除两个或者更多的点才能破坏这个大于$d$的距离，所以贪心策略即从叶结点往上搜，一旦遇到往下的最大距离大于$d$,就删掉这个结点

实现

采用邻接表存图，$dfs$算点往下的最大距离，从下往上算

删点

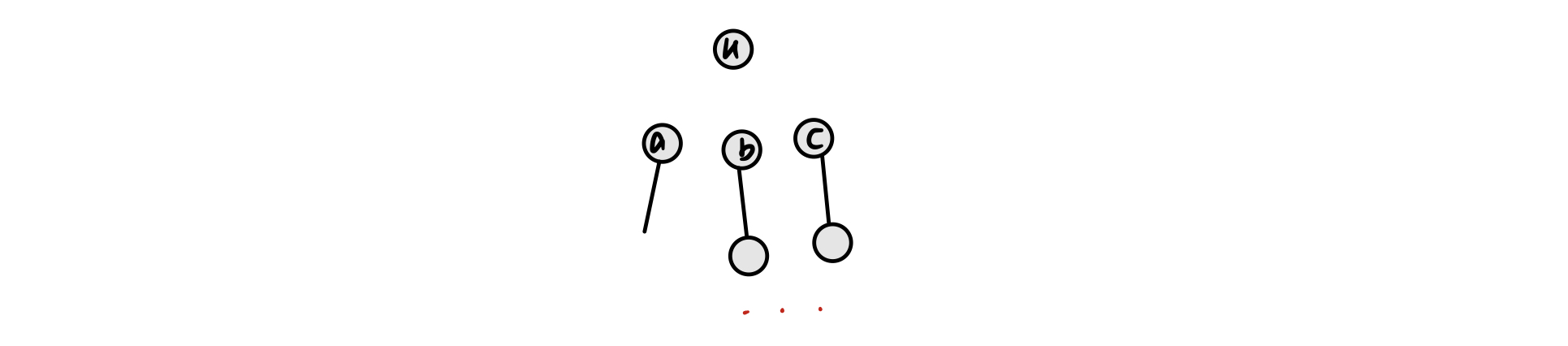
如下图，假设$u$->$a$为$u$往下的最长路径且距离大于$d$，那么根据上面可知我们要将$u$给删去

删去后如下图，但是删除$u$后我们只能保证$u$->$a$这条大于$d$的路径被删除了，并不能保证$b$,$c$作为父节点往下是否存在大于$d$的路径，所以我们删除u后不能直接$return$(这里调了一万年😭😭😭)
因为我们将$u$删除等价于对u的父节点来说$w+dfs(u)$为$0$($w$为$u$的父节点到$u$的距离)，所以我们只需要在遍历完$u$的所有子节点后返回一个很大的负数即可，在维护$u$的父节点的往下最大值的和$0$去$max$即可达到删除$u$的效果(注意是加上$w[i]$后再和$0$取$max$)

Code

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4+10;
int n, d, ans;
int h[N], e[N], ne[N], w[N], idx;
bool st[N];
void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
int dfs(int u)  // 求u往下的最长距离
{
    int res = 0;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        int dis = dfs(j);  // 先算子树
        if (!st[u]) dis = max(dis + w[i], 0);
        if (dis > d && !st[u]) // 如果u->j...的距离大于d，就应将u删除  只考虑删一次u(st[u]=false时)
        {
            ans ++;
            st[u] = true;  // 将u删除
            continue;
        }
        res = max(res, dis);
    }
    if (st[u]) return -2e9;
    else return res;
}
int main()
{
    cin >> n >> d;
    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i ++)
    {
        int k; cin >> k;
        while (k --)
        {
            int a, b; cin >> a >> b;
            a ++;  // 从1开始编号
            up[a] = b;  // 记录a到直接父节点的距离为b
            add(i, a, b);
        }
    }
    dfs(1);
    cout << ans; 
    return 0;
}