算法基础课听的不是很牢固,故听算法提高的时候边整合算法基础的内容,之后边学习边复习完善,同时补全语法基础的细节,并把相关的题目(leetcode和acwing)整理成题单,方便复习和强化思路,之后整理出一系列的总结

动态规划是算法学习中很难的部分,故听完算法基础课仿佛没听一样,还好提高课量大,帮助我理解

线性dp

状态之间有线性关系的动态规划问题。

线性dp包括数字三角形模型,最长上升子序列问题等

数字三角形模型

先说总结和核心:该类问题的一般突破口在最后的状态递推到之前的状态

• acwing 898 数字三角形
  先用闫氏dp分析,求max并且集合是从(1,1)到最底层的最大路径,
  先简化数字三角型的图,变成比较好定位的图(何必为难自己),具体见图一
  
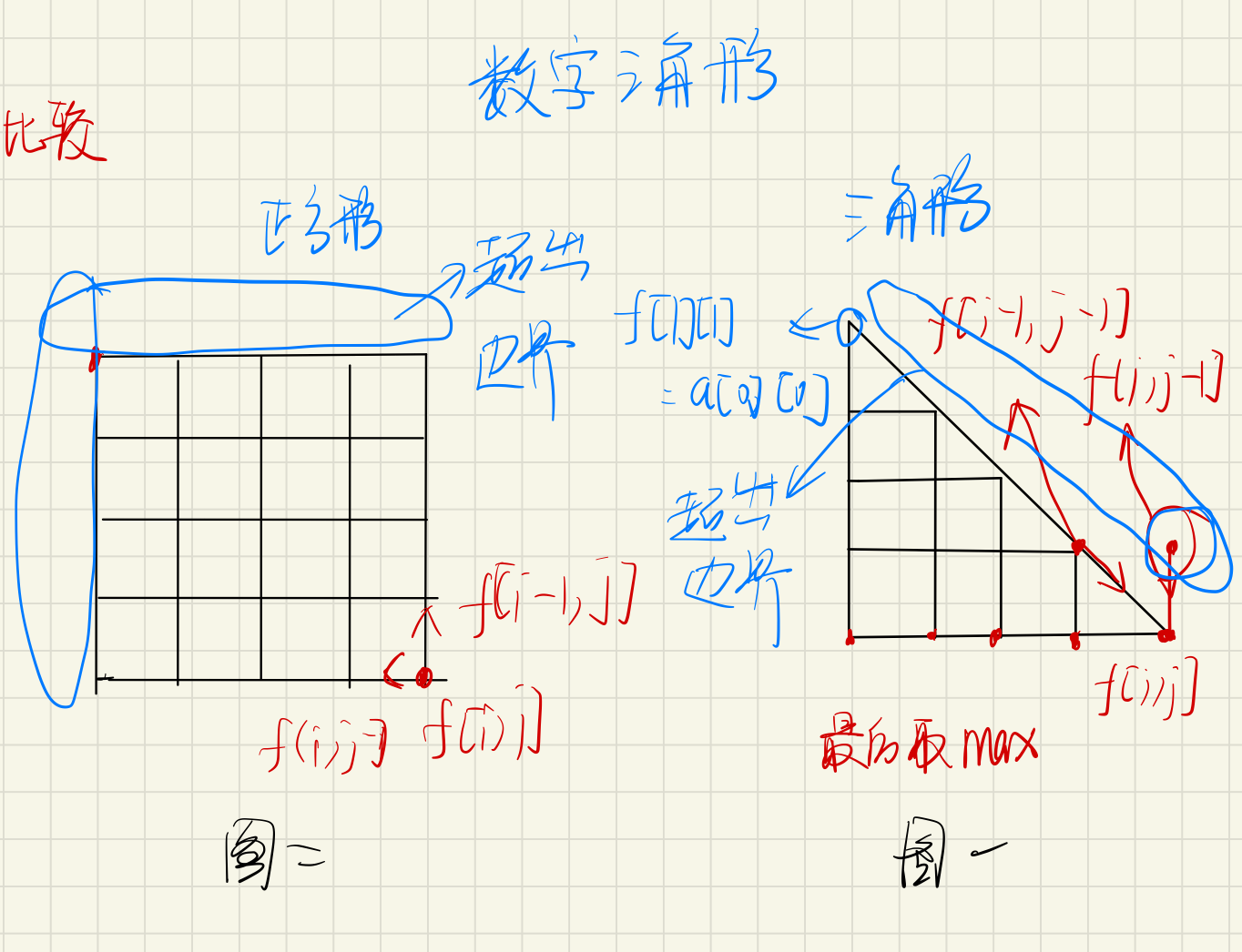
  核心代码: f[i][j] = max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j])
  需要注意的是边界条件,已经超过了所给的值,故需要初始化数组和边界条件
  注意: f[1][1] = a[1][1]; //注意初始化
  由题意,最后要对最后一行取max

• acwing 1015 摘花生
  见图二,与数字三角形进行比较,同属于max的属性,思路相同,但形状不一样
  核心代码: f[i][j] = max(f[i - 1][j], f[i][j - 1]) + a[i][j];
  该题只需要走到最后,并且是max型,故不需要初始化,直接输出

• AcWing 1018. 最低通行费
  该题和上一题的唯一区别就在于min,可用 for(int i = 2;i<=n;i++)f[0][i] = 1e9; for(int i = 2;i<=n;i++) f[i][0] = 1e9; 进行初始化值,其它类似处理

• AcWing 1027. 方格取数
  这题就在原模型上进行了综合应用,有提高课的难度,该问题的重要的地方在于将原先的一条路径推广到2条路径,从这题我们还可以到很多条,即将数组扩大的相应的维数,用来描述状态
  该题的思路:需要同时描述两条路线的路径(如果分开用st数组的话,所求的不是最大的,可能有漏的情况),k的使用是一个很妙的参数,通过k可以实现同步,有bfs的思想
  小技巧:&引用可以边更新x边更新f相对应的值
  核心代码:

for (int k = 2; k <= n + n; k ++ )
        for (int i1 = 1; i1 <= n; i1 ++ )
            for (int i2 = 1; i2 <= n; i2 ++ )
            {
                int j1 = k - i1, j2 = k - i2;
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
                {
                    int t = w[i1][j1];
                    if (i1 != i2) t += w[i2][j2];(如果没有重合,就加上第二个路径)
                    int &x = f[k][i1][i2];
                    x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1 - 1][i2] + t);
                    x = max(x, f[k - 1][i1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1][i2] + t);
                }
            }

• AcWing 275. 传纸条
  该题和方格取数本质是相同的,来回和去两趟实际上是相同的(前提是取最大值),有个证明非常妙,证明传纸条为何可以使用方格取数的代码 ,就是三角不等式两边之和大于第三边
  详细见图: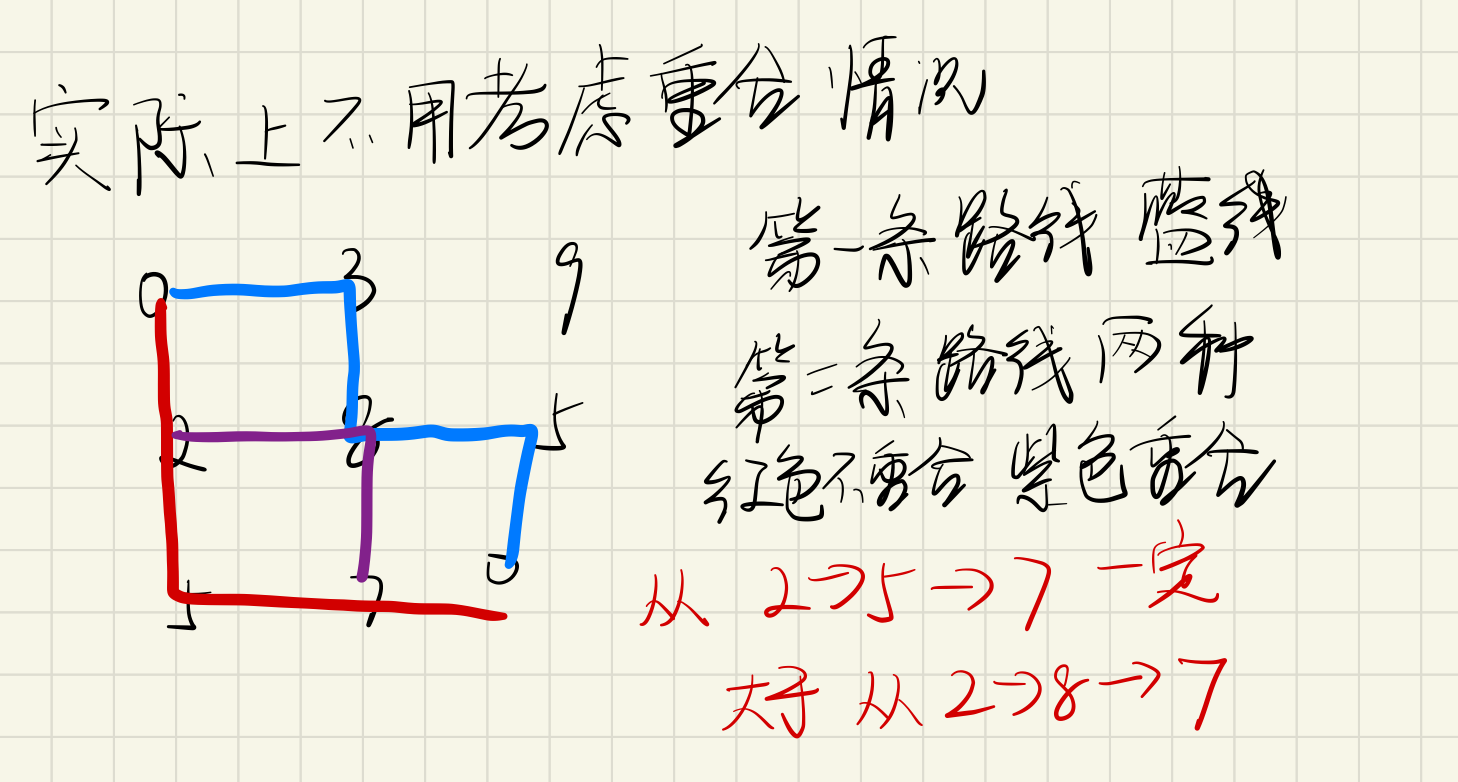

最长上升子序列问题

• 模型来历:AcWing 895. 最长上升子序列
  模板思路:闫氏dp法:以第i个数结尾的上升子序列作为划分依据(主要还是最后的情况往前递推),这样划分的好处是可以做到不重不漏
  模型代码

for(int i = 1;i<=n;i++)
    {
        f[i] = 1;
        for(int j = 1;j<=n;j++)
            if(a[i] > a[j])
                f[i] = max(f[i],f[j]+1);
    }

模型变化:

• AcWing 1017. 怪盗基德的滑翔翼
  三种情况
  
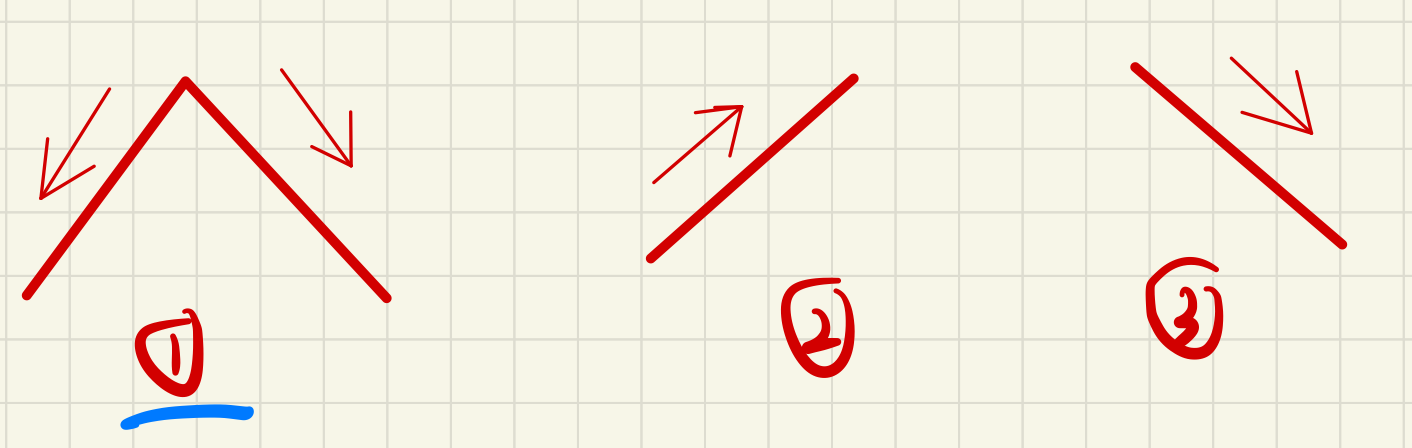
  但是只能往一边飞,所以其实想找最多的建筑,只能在第二和第三种情况,可以与下一道题比较.所以代码就是正着输一遍,再反着输一遍

• AcWing 1014. 登山
  
  这题的思路与上一题可以进行比较,这题是先上再下,上题是可上可下
  所以代码是两边往上dp一遍,对每个顶峰用f[k]+g[k]-1得到答案