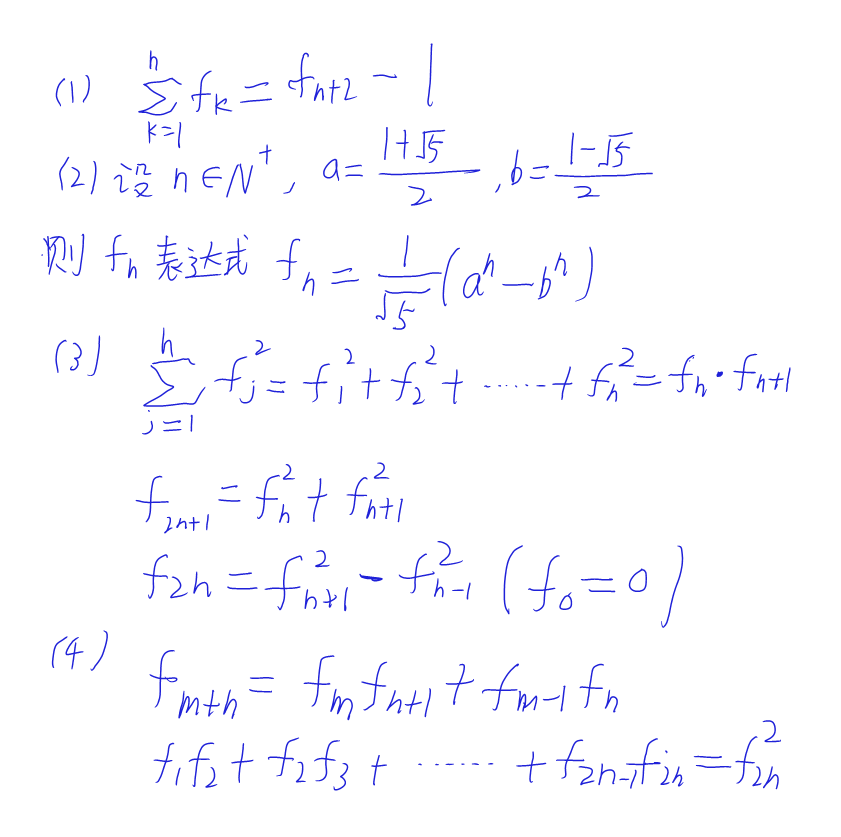# 一、整数
1.良序性质：每个非空的正整数集合都有一个最小元
2.有理数：如果存在整数p和q!=0,使得r=p/q,则称实数r是有理数，如果r不是有理数，则称为无理数。
3.代数数与超越数：如果某个数a是整系数多项式的根,即a是方程p1*x^n+p2*x^(n-1)+……pn=0关于x的一个根，则称其为代数数，否则a就是超越数。
4.最大整数函数(C++的floor函数)：即不超过x的最大正整数，记为[x],满足[x]<=x<=[x]+1。C++常用取整函数为上取整函数ceil和下取整函数floor,包含在<cmath.h>中。
y=[x]函数有如下性质：
(1)x-[x]可以求x的小数部分。(不过C++要注意精度，比如保留2位小数在后面加上0.00，三位小数就加上0.000,诸如此类,否则结果可能为0,后面不再赘述精度问题)
(2)[x]+[-x]=1,[x]+[x+1/2.0]=[2*x]对于任意实数x恒成立。
(3)[x+y]>=[x]+[y],[2x]+[2y]>=[x]+[y]+[x+y]对于任意实数x和y恒成立。
(4)当x为实数时,-[-x]是大于等于x的最小整数。
(5)通常的四舍五入表示可以写成[x+1/2]。
(6)当x为非负实数时，[sqrt([x])]=[sqrt(x)]。
(7)当m为正整数，则当x为实数时，[mx]=[x]+[x+1/m]+[x+2/m]+……[x+(m-1)/m]。

5.三大逼近原理
鸽笼原理：如果把大于等于k+1个物品放入k个盒子中，那么至少有一个盒子中有两个或者更多物体。
狄利克雷逼近原理：如果k是一个实数，n是一个正整数，则存在正整数a和b,使得|k*a-b|<1/n。
丢番图逼近原理：对于一个无理数a，存在无数多个不同的有理数p/q使得|a-p/q|<1/q^2。
6.可数与不可数：对于一个集合，如果这个集合元素个数是有限的，或者个数是无限的但与正整数集合之间存在一个映射，则称该集合为可数的，否则该集合就是不可数的。
    有理数集合是可数的，但是实数集合是不可数的。



## 
二、斐波那契数列fn
1.定义：f1=1,f2-1,当n>=3时，有fn=fn-1+fn-2。
2.斐波那契性质：