1. 概述
1.1 决策树的工作过程
决策树是一种用于分类和回归的非参数有监督学习方法;
其目标是创建一个模型,通过学习从数据特征中推断出的简单决策规则预测目标变量的值;
决策树算法的核心问题:
1)如何从数据表中找出最佳节点和最佳分支;
2)如何让决策树停止生长,防止过拟合;
1.2 sklearn中的决策树
sklearn中的决策树都在tree模块下
tree.DecisionTreeClassifier() 分类树
tree.DecisionTreeRegressor() 回归树
tree.export_graphviz() 将生成的决策树导出为DOT格式,用于画图
tree.ExtraTreeClassifier() 高版本的分类树
tree.ExtraTreeRegressor() 高版本的回归树
1.3 决策树中的参数解释
clf = tree.DecisionTreeClassifier(
criterion="gini",
splitter="best",
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.,
max_features=None,
random_state=None,
max_leaf_nodes=None,
min_impurity_decrease=0.,
min_impurity_split=None,
class_weight=None,
ccp_alpha=0.0)
1.3.1 criterion
将表格转化为一棵树,需要决策树找到最佳结点和最佳分枝方法;
衡量这个最佳的方法是基于节点的‘不纯度’,不纯度越低,决策树拟合效果越好
entropy : 使用信息熵
gini : 使用基尼系数 默认
两者使用过程中基本无区别
比起基尼系数,信息熵对于不纯度更加敏感,惩罚力度最强,决策树的生长会更加精细;对于高维度或者噪声多的数据,信息熵容易过拟合,基尼系数这方面表现比较好;
1.3.2 random_state
决策树在建树时,靠的是优节点形成一个优化的树;
优化结点相当于得到局部最优解,但局部最优不一定得到全局最优;
因此,不如建立多个不同的树,然后从中选取最优的一个;
sklearn在每次分枝时,不会使用全部特征,而是会随机选取一部分特征,从中选取指标最优的作为分支节点,每次生成的树也就不一样;
这也是randon_state参数的作用
用于设置分支中的随即参数的模式,默认为None;
这样每次生成的就会是同一个树
1.3.3 splitter
splitter也是用老控制决策树中随即选项的
best : 决策树分枝时虽然随机,但是会优先选择最重要的特征进行分支(feature_importance查看)
random : 决策树分枝时会更加随机,树会因为不必要的信息更深更大,会因为不必要的信息降低拟合程度;
这两个参数会降低过拟合的可能性;
后面还有剪枝方法在树建成后防止过拟合
剪枝参数
1.3.4 max_depth
限制树的最大深度,超过深度的全部剪掉,可以有效防止过拟合;
建议从3开始剪枝;
1.3.5 min_samples_split
限定一个节点必须含有min_samples_split个样本,节点才允许分枝;
结果:有分枝的节点样本至少是min_samples_split个
1.3.6 min_samples_leaf
限定一个节点在分枝后的每个子节点都必须包含至少min_samples_leaf个节点;
结果:决策树的所有节点都至少包含min_samples_leaf个节点;
树的精修
1.3.7 max_features
max_features限制分枝时候考虑的特征个数,超过个数的特征都会被舍弃;
用来限制高维度数据过拟合时的剪枝参数,属于暴力的直接限制;
在不知道各个特征重要性情况下,PCA等降维算法会更加合适;
1.3.8 min_impurity_decrease
限制信息增益的大小;
信息增益小于设定数值的分枝不会发生;
之前版本是:min_impurity_split
目标参数权重
class_weight:
完成样本平衡的参数;
对样本标签进行一定的均衡,加大少数类样本的话语权
min_weight_fraction_leaf
搭配class_weight使用,因为有了权重后,样本量不单单指的数目,而会收到权重影响;
作为基于权重的剪枝参数,将比min_samples_leaf更少偏向主导类,更容易优化树结构;
1.4 决策树的特点:
1.4.1 优点
- 易于解释和理解,树可以被可视化;
- 几乎不需要数据准备(如数据标准化)
- 可以处理数值型和分类型数据;
- 可以处理多输出问题
- 使用白盒模型,给定情况可以观察得到,对条件的解释容易用布尔逻辑解释(类似人工神经网络的黑盒模型很难解释)
1.4.2 缺点:
- 决策树学习器可以创建非常复杂的树,容易过拟合,所以需要剪枝叶,设置叶节点所需最小样本或者设置树的最大深度;
- 决策树可能是不稳定的,数据中小的变化可能导致生成完全不同的树,可以通过集成决策树缓解;
2. 分类决策树
2.1 初步构建
1.导入需要的算法库和模板
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn import tree
2.对数据集获取
iris_data = load_iris()
3.分为训练集和测试集
x_train,x_test,y_train,t_test = train_test_split(iris_data.data
,iris_data.target
,test_size=0.3
,random_state=22)
4.建立模型
clf = tree.DecisionTreeClassifier()
clf.fit(x_train, y_train)
5.打分
clf.score(x_test,t_test)
重要的接口与属性
feature_importances_
fit : 训练模型(输入的特征矩阵必须是一个二维矩阵,哪怕只有一个特征,目标值输入一维向量)
score(x_test,y_test) : 用测试集给模型打分
apply(x_test) : 返回每个测试样本所在叶子节点的索引
predict(x_test) : 返回每个测试样本的标签
predict_proba(x_test) : 可以预测其它样本的类别
tree.plot_tree(clf)
可以可视化决策树,但是非常难看

所以导入grapgviz库可视化决策树;
2.2 grapgviz可视化
2.2.1 grapviz的安装
下载anaconda
conda install python-graphviz
2.2.2 决策树的展示
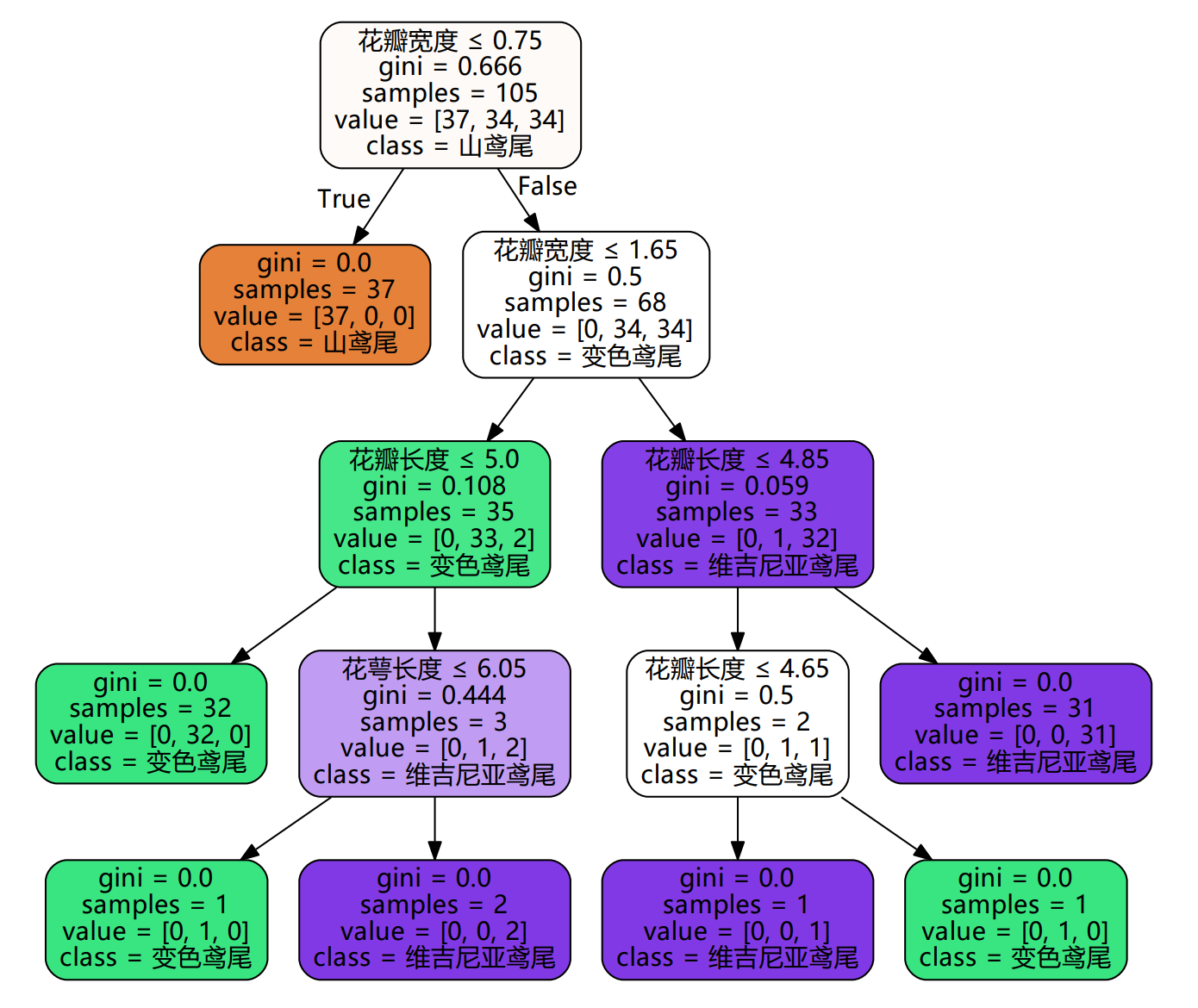
import graphviz
dot_data = tree.export_graphviz(clf
,out_file=None
,feature_names=["花萼长度","花萼宽度","花瓣长度","花瓣宽度"]
,class_names=['山鸢尾','变色鸢尾','维吉尼亚鸢尾']
,filled=True
,rounded=True
,special_characters=True
)
graph = graphviz.Source(dot_data)
graph
graph.render("iris")
这行代码会把决策树保存到一个pdf文件,format参数改变默认格式
问题:保存的pdf文件会有中文乱码
解决方法:
graph = graphviz.Source(dot_data.replace('helvetica','"Microsoft YaHei"'), encoding='utf-8')
graph.render('iris_DT')
3. 回归决策树
3.1 概述
与分类树非常类似,只是y在这里是浮点类连续型
3.2 重要参数与属性
3.2.1 criterion
mse : 使用的是均方误差,该方法使用叶子结点的均值来最小化L2损失;
friedman_mse : 改进后的均方误差
mae : 绝对平均误差,使用叶节点的中值最小化L1损失
回归树接口score返回的是R^2不是mse
from sklearn.datasets import load_boston
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor
boston = load_boston()
regressor = DecisionTreeRegressor(random_state=22)
cross_val_score(regressor
,boston.data
,boston.target
,cv=10
,scoring="neg_mean_squared_error"
)
3.3 实例:一维回归图像
# 1.导入需要的库
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
# 2.创建一条含有噪声的正弦曲线
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80,1),axis = 0)
y = np.sin(X).ravel()
# 创建噪声
y[::5] += 3 * (0.5 - rng.rand(16))
# 3.实例化训练模型
estimator1 = DecisionTreeRegressor(max_depth=2)
estimator2 = DecisionTreeRegressor(max_depth=5)
estimator1.fit(X,y)
estimator2.fit(X,y)
# 4.测试集导入模型
x_test = np.arange(0.0,5,0.01)[:,np.newaxis]
y_1 = estimator1.predict(x_test)
y_2 = estimator2.predict(x_test)
# 5.绘制图像
plt.figure()
plt.scatter(X,y,s=20
,c='darkorange'
,edgecolors='black'
,label='data')
plt.plot(x_test,y_1
,color='purple'
,label='max_depth=2')
plt.plot(x_test,y_2
,color='green'
,label='max_depth=5')
plt.legend()
plt.show()

