总结:学习新的东西和技巧才重要，不要太在意成绩

1.统计子矩阵

通过挖掘题目的性质，一步步优化时间复杂度
赛时：也在不断优化，不过也只能优化到n^3logn,发现其实和n^4差别不大，只能说离最后的正解，只差了一步

$O(n^6)$(6个暴力for循环)---->$O(n^4)$(二维前缀和优化)—>$O(n^3logn)$(前缀和+二分)—>$O(n^3)$(前缀和+双指针)

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=510;
LL s[N][N];
int n,m;
LL k;

bool check(int x,int l,int r,int y)
{
    LL sb=s[x][r]-s[x][l-1]-s[y-1][r]+s[y-1][l-1];
    return sb<=k;
}

int main()
{
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            LL x;
            scanf("%lld",&x);
            s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+x;
        }
    }
    //思路枚举矩形左右边界 
    LL ans=0;
    for(int i=1;i<=m;i++)
    {
        for(int j=i;j<=m;j++)
        {
            //双指针
            for(int l=1,r=1;l<=n;l++)
            {
                while(!check(l,i,j,r))r++;
                ans+=l-r+1;
            } 
        }
    }
    cout<<ans;
    return 0;
}

2.李白打酒加强版

dp题如何去合理的设计dp的状态表示，以及如何更好的，更直观的进行状态转移，这是我这道题学到的技巧

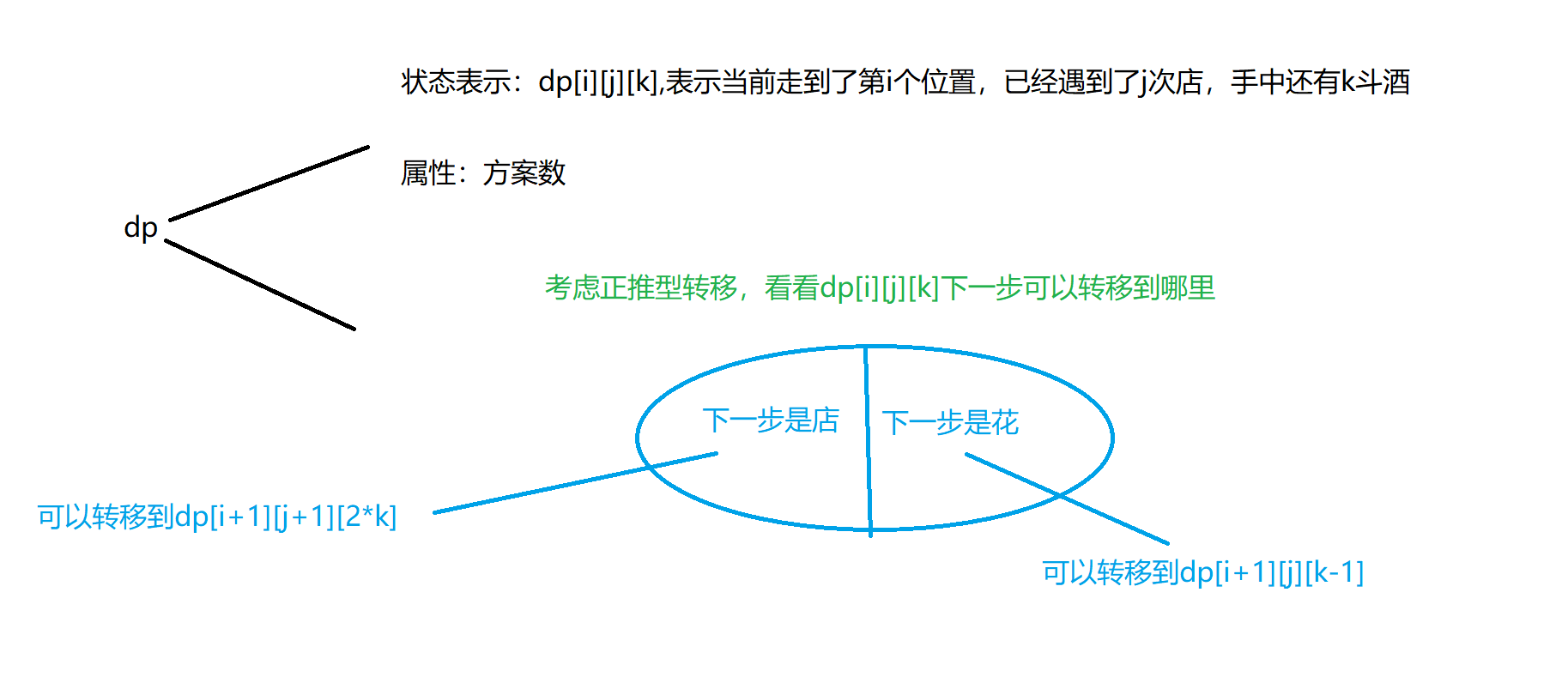
赛时：当时看到要求方案数，而且方案数很多时，就想到了dp，但这dp的状态表示和状态转移的多样化，让我在赛时想了很久，一开始想的四维dp[i][j][k][u],表示考虑前i个位置，已经遇到了j次店，k次花，手中有u斗酒,但后来发现空间可能爆了，所以优化成了三维dp，但发现状态转移依然要4个for循环，感觉还是超时，然后就一直想不到一个合理的状态表示，所以赛时实在没办法只能最后写了一个dfs交了发暴力

合理的dp表示：后来赛后一想，好像花和店不需要同时在状态表示里，如果我表示了前i个位置，j次店，有k斗酒，这样也可以达到转移的目的，因为酒的数量和店有关，而且我们发现一个位置不是店就是花，当我们走完n+m步，而且遇到了n次店，就已经说明我的状态是也已经遇到了m次花，所以只需要三维dp，然后$O(n^3)$的复杂度就可以进行状态转移,而且我们可以发现其实酒在不断加倍的过程中，它如果很大的时候，我们这个时候花的限制已经不管用，因为我的酒根本就喝不完，所以其实酒的最大值不用很大，当走到一个位置的时候，酒已经>花的数量，那么我的酒肯定是喝不完了

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL dp[210][110][310];
const LL mod=1e9+7;
int n,m;

int main()
{
    cin>>n>>m;

    dp[0][0][2]=1;
    for(int i=0;i<=n+m;i++)
    {
        for(int j=0;j<=n;j++)
        {
            for(int k=0;k<=210;k++)
            {
                if(2*k<=210)dp[i+1][j+1][2*k]=(dp[i+1][j+1][2*k]+dp[i][j][k])%mod;
                if(k>=1)dp[i+1][j][k-1]=(dp[i+1][j][k-1]+dp[i][j][k])%mod;
            }
        }
    }
    //因为最后一步要是花，所以是dp[n+m-1][n][1],前n+m-1步遇到了n次店，手中还有1斗酒，然后最后一步会喝完这斗酒
    cout<<dp[n+m-1][n][1];  
    return 0;
}

3.扫雷

卡常题，很容易就会TLE(卡map，需要用自己写哈希或者转化成unordered_map)，学习到的新东西：通过数据合理枚举，发现半径r<=10，所以我们枚举半径来搜索点,以及题目中说了有重合的雷，为了减少搜索量，我们考虑合并雷，保留重合雷中半径最大的那个

赛时：没有想到枚举半径，所以只能枚举了所有炸雷，所以只能过40%样例

代码还没过全部样例，已经转化把坐标映射到一个值，然后用unordered_map,但是还是被卡了，感觉还是得是手写哈希表

//被卡常了，可能unordered_map也不太行，估计要手写哈希了


#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10;
typedef long long LL;
typedef pair<LL,LL>PII;
struct node
{
    LL x,y,r;
    int sum;
};
node a[N],b[N];
unordered_map<LL,int>ma,mb; //存对应点的下标 
bool st[N];
int n,m;

LL get(LL x,LL y){
    return x*(1e9+7)+y;
}

LL pf(LL x,LL y){
    return abs(x-y)*abs(x-y);
}

void dfs(LL x,LL y,LL r)
{

    //枚举半径
    for(int i=-r;i<=r;i++){
        for(int j=-r;j<=r;j++){
            LL ux=x+i,uy=y+j;
            LL gg=get(ux,uy);
            if(!ma.count(gg))continue;
            int sb=ma[gg];
            if(!st[sb]&&pf(ux,x)+pf(uy,y)<=r*r){
                st[sb]=true;
                dfs(ux,uy,a[sb].r);
            }
        }
    } 


}


int main()
{


    scanf("%d%d",&n,&m);
    int cnt=0; //存下标 
    for(int i=1;i<=n;i++){
        LL x,y,r;
        scanf("%lld%lld%lld",&x,&y,&r);
        LL gg=get(x,y);
        if(!ma.count(gg)){ //没出现过 
            ma[gg]=cnt;
            a[cnt++]={x,y,r,1};
        }
        else{
            int sb=ma[gg];
            a[sb].sum++; //合并坐标相同的 
            a[sb].r=max(a[sb].r,r);
        }
    }
    int cmp=0;
    for(int i=1;i<=m;i++)
    {
        LL x,y,r;
        scanf("%lld%lld%lld",&x,&y,&r);
        LL gg=get(x,y);
        if(!mb.count(gg)){ //没出现过 
            mb[gg]=cmp;
            b[cmp++]={x,y,r,1};
        }
        else{
            int sb=mb[gg];
            b[sb].sum++; //合并坐标相同的 
            b[sb].r=max(b[sb].r,r);
        }
    }

    for(int i=0;i<cmp;i++){
        LL x=b[i].x,y=b[i].y,r=b[i].r;
        dfs(x,y,r);
    }

    int ans=0;
    for(int i=0;i<cnt;i++)if(st[i])ans+=a[i].sum;
    cout<<ans;

    return 0;   
} 

4.积木画

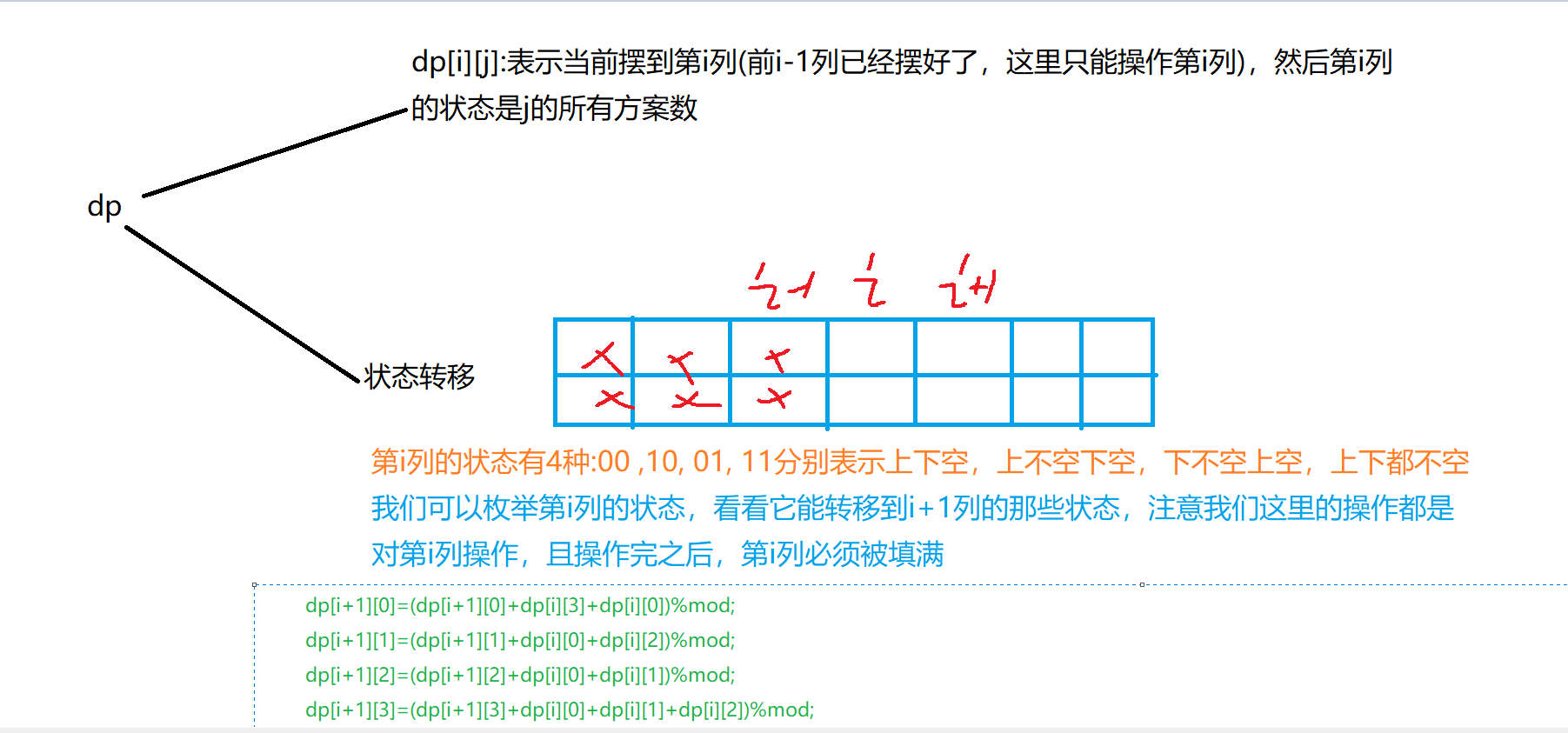
状压dp，棋牌式类型的状压dp

赛时：由于不太会状压dp，所以只能找规律，推递推式，后来推了半天，然后验证了前几项，感觉对了，然后就交了，赛后发现其实递推式的根本不对，感觉只是碰巧满足前几个而已，呜呜！

#include<bits/stdc++.h>
using namespace std;
const int N=1e7+10;
typedef long long LL;
LL dp[2][4];
const int mod=1e9+7;
int main()
{
    int n;
    cin>>n;
    dp[1][0]=1;
    //滚动数组优化 
    for(int i=1;i<=n;i++)
    {
        memset(dp[i+1&1],0,sizeof dp[i+1&1]);
        dp[i+1&1][0]=(dp[i+1&1][0]+dp[i&1][3]+dp[i&1][0])%mod;
        dp[i+1&1][1]=(dp[i+1&1][1]+dp[i&1][0]+dp[i&1][2])%mod;
        dp[i+1&1][2]=(dp[i+1&1][2]+dp[i&1][0]+dp[i&1][1])%mod;
        dp[i+1&1][3]=(dp[i+1&1][3]+dp[i&1][0]+dp[i&1][1]+dp[i&1][2])%mod;
    }
    cout<<dp[n+1&1][0]%mod<<endl;
    return 0;
}