Acwing1073.树的中心

树的中心即数所有点中到其他点最远距离最近的点

树形$dp$

数的最长直径中求的是直径的长度，没有具体求直径的“圆心”。本题要求出具体“圆心”到其他点的最远距离，所以我们只需要在该题的思路上稍加修改即可。

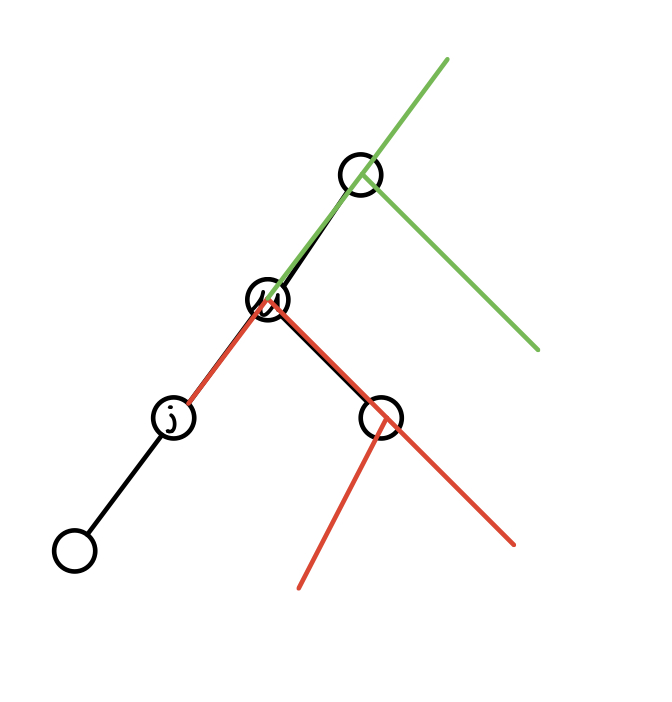
对于每个点，单有向下的最长距离还不够，我们还需要知道向上的最长距离，才能判断哪一个点直径最大
所以我们还需要从上向下进行一次树形DP。以u及u的一个子节点j为例，记录w[u][j]为u与j之间的距离。对于j，它
的向上的最大距离可以分为过父u后继续向上和过u后开始向下两种：
① 过u后继续向上，那么j向上的距离up[j] =  w[u][j] + up[u]
② 过u后开始向下，那么j向上的距离就为w[u][j]加u开始向下的距离。父节点向下的距离也可以分为过子节点j和不
过子节点j两种：
  1° 过j。如果过j，那么则不能u点最长的向下的路径(与j向下的最长路径重复了)，所以选u向下的次长距离d2 
  up[j] = w[u][j] + max(d2[u], up[i]
  2° 不过j。那么就可以直接选中u向下的最长路径。up[j] = w[u][j] + d1[u]
所以更新方式为：
if (pt[u] == j) up[j] = max(up[u], d2[u]) + w[i]);
else up[j] = max(d1[u], up[u]) + w[i];
由此可见我们在更新每个点向下的最长距离的时候还需要记录具体是通过哪个点向下。

要注意的细节：

① 因为$dfs$_$up$的时候向下的距离相关数据已经算出来了，所以只需要从上往下遍历一遍取最值即可，$father$作用仅是保证一直往下层计算

② 根节点没有向上的直径，$up[1]=0$，不能也去和$ans$取$min$，会导致为$0$

③ 本题中没有负边权，如果有负边权，那么$dfs$的时候要将距离数组初始化为$-INF$，在$dfs$最后加上如果没有更新$-INF$则是叶结点，将距离数组值置$0$

时间复杂度$O(N)$

#include<bits/stdc++.h>
using namespace std;
const int N = 20010;

int d1[N], d2[N], pt[N], up[N];
int h[N], e[N], ne[N], w[N], idx;
void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

int dfs_down(int u, int father)
{
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        int distance = dfs_down(j, u) + w[i];
        if (distance > d1[u]) d2[u] = d1[u], d1[u] = distance, pt[u] = j;
        else if (distance > d2[u]) d2[u] = distance;
    }
    return d1[u];
}
void dfs_up(int u, int father)  // 这里是用u当父节点，去更新u的子节点的up[]信息，father仅是保证从上往下计算
{
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        if (pt[u] == j) up[j] = max(up[u], d2[u]) + w[i];
        else up[j] = max(d1[u], up[u]) + w[i];
        dfs_up(j, u);
    }
}

int main()
{
    int n; cin >> n;
    memset(h, -1, sizeof h);
    for (int i = 0; i < n; i ++)
    {
        int a, b, c; cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
    dfs_down(1, -1);
    dfs_up(1, -1);
    int ans = d1[1];  // 因为根节点没有向上的路径，所以单独取d1
    for (int i = 2; i <= n; i ++) ans = min(ans, max(up[i], d1[i]));
    cout << ans;

    return 0;
}