在我初学算法的时候把这本书看过一遍，但当时基础太差根本无法领会其精要。最近得闲翻了一下，发现确实是本好书，一边看一边记录吧。

一、排序

在接下来介绍的各种排序中，我们以 排序数组 这个题为例进行代码的性能测试。

1.1、选择排序

1.1.1 实现思路

• 首先找到数组中最小的元素，将它与第一个元素交换位置，再从剩下的数中找到最小的元素，将它与第二个元素交换位置，如此反复，直到将整个数组排序；

• 选择排序需要进行大约 $O(N^2/2)$ 次比较以及$O(N)$次交换；

• 特点：运行时间与输入数据无关，数据移动是最少的，只需要N次交换操作。

1.1.2 代码

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        for (int i = 0; i < nums.size(); ++ i)
        {
            int minIdx = i;
            for (int j = i + 1; j < nums.size(); ++ j)  //第二重循环找剩余数组中的最小值下标
            {
                if (nums[j] < nums[minIdx])
                {
                    minIdx = j;
                }
            }

            swap(nums[i], nums[minIdx]);                //找到后与当前元素进行替换
        }

        return nums;
    }
};

1.2 插入排序

1.2.1 实现思路

• 遍历数组，将元素插入到前面已排好序的数组中，后面的元素需要全都往后挪一个位置；

• 最坏的情况下（输入数组为逆序），需要进行$O(N^2/2)$次比较和$O(N^2/2)$次交换；最好的情况下（输入数组为有序），需要进行$O(N-1)$次比较和 $0$ 次交换；

• 特点：运行时间与输入数据有关（有序数组最快，逆序数组最慢）；

• 插入排序适用的情况：
  1、 数组中每个元素距离它的最终位置都不远；
  2、 一个有序的大数组接一个小数组；
  3、 数组中只有几个元素的位置不正确。

1.2.2 代码

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        for (int i = 0; i < nums.size(); ++ i)
        {   
            //第二重循环把当前较小元素往前一直挪到合适的位置
            for (int j = i; j > 0 && (nums[j] < nums[j - 1]); -- j)
            {
                swap(nums[j], nums[j - 1]);
            }
        }

        return nums;
    }
};

1.3 希尔排序

1.3.1 实现思路

• 该算法在插入排序的基础上，增加了一个h参数，即先将数组中任意间隔为h的元素排序，使之成为h有序数组，见下图。h值会慢慢变小，当h=1时希尔排序完全等于插入排序；

• 可以将希尔排序看成是在插入排序前对数据进行了一些预处理操作，将每个数值大致划分到各自的值域范围内。最后进行插入排序时，就不会出现把最后一个元素移动到最前这种低效的操作了，即刚好满足插入排序适用的第一种情况：数组中每个元素距离它的最终位置都不远；

• 透彻理解希尔排序的性能至今仍然是一项挑战，但它性能是优于前两种排序的，且数组越大优势越大。

1.3.2 代码

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int h = 1;
        while (h < nums.size() / 3) h = 3 * h + 1;  //书中所写初始h值的取法

        while (h >= 1)  //h值会慢慢变小，最终为1，当h=1时即完全等于插入排序
        {
            for (int i = h; i < nums.size(); ++ i)
            {
                for (int j = i; j >= h && nums[j] < nums[j - h]; j -= h)
                {
                    swap(nums[j], nums[j - h]);
                }
            }
            h /= 3;
        }
        return nums;
    }
};

1.4 归并排序

1.4.1 实现思路

• 归并排序分为自顶向下与自底向上两种，后者比较适合用链表组织的数据；
• 归并排序性能是非常稳定的，对于任意输入数据，它的时间复杂度都是$O(NlogN)$，它的主要缺点是需要$O(N)$的额外空间；
• 改进点：使用插入排序处理小规模子数组，一般可以将归并排序的运行时间缩短10%~15%。

1.4.2 代码

class Solution {
private:
    vector<int> aux;

public:
    void merge(vector<int>& nums, int lo, int mid, int hi)
    {
        int i = lo, j = mid + 1;        //i，j分别为两段有序子数组的起始下标

        for (int k = lo; k <= hi; ++ k) aux[k] = nums[k];       //拷贝到辅助数组

        for (int k = lo; k <= hi; ++ k)
        {
            if (i > mid)                nums[k] = aux[j ++ ];   //左半边数组用尽（取右半边的元素）
            else if (j > hi)            nums[k] = aux[i ++ ];   //右半边数组用尽（取左半边的元素）
            else if (aux[i] < aux[j])   nums[k] = aux[i ++ ];   //左半边当前元素小于右半边当前元素
            else                        nums[k] = aux[j ++ ];   //右半边当前元素小于左半边当前元素
        }
    }

    void mergeSort(vector<int>& nums, int lo, int hi)
    {
        if (hi <= lo) return;
        int mid = lo + (hi - lo) / 2;
        mergeSort(nums, lo, mid);       //自顶向下分割进行排序
        mergeSort(nums, mid + 1, hi);
        merge(nums, lo, mid, hi);
    }

    vector<int> sortArray(vector<int>& nums) {
        aux.resize(nums.size());

        mergeSort(nums, 0, nums.size() - 1);

        return nums;
    }
};

1.5 快速排序

1.5.1 实现思路

• 选择数组中一个数来做切分，将整个数组分为比这个数大和比这个数小的两个部分，递归地划分直到子数组长度为1为止；
• 快排的效率很大程度取决与划分的点在数组中是否为中位数，若每次划分刚好能把数组分成等长的两部分，则是最好的情况，时间复杂度为$O(NlogN)$，最坏的情况下时间复杂度为$O(N^2)$，即每次划分都选到最边缘的值；
• 快排改进点：
  1、 在开始排序前随机地将数组打乱，虽然会占用排序的一大部分时间，但能够防止出现最坏情况并使运行时间可以预计，这是值得的；
  2、 在划分到较短子数组时切换成插入排序，子数组长度取在5~15之间都能得到令人满意的结果；
  3、 三数取中，取数组前中后三个数的中位数来进行划分，可以尽量避免取到边缘值；
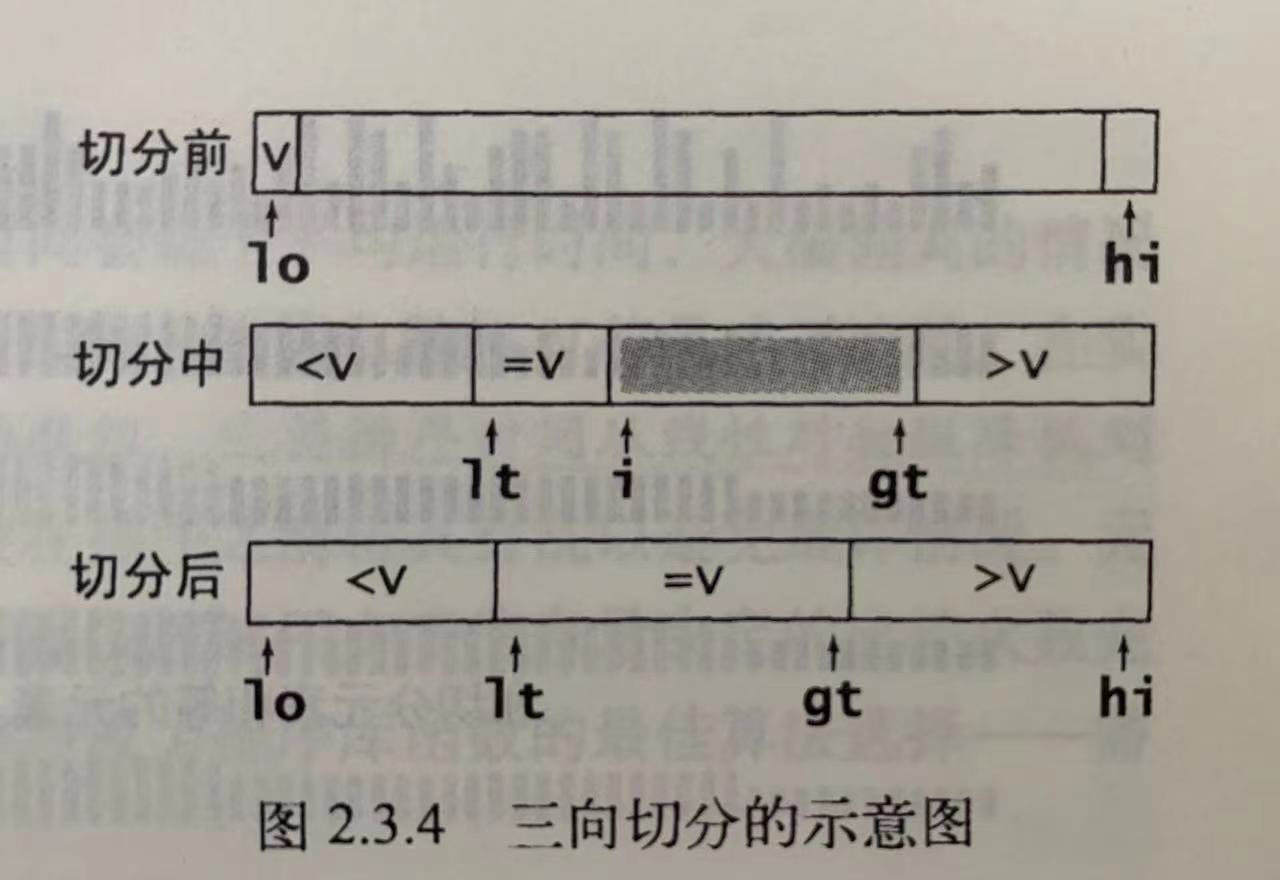
  4、 针对大量重复值的数组采用三向切分法，将数组切成小于、等于、大于切分点的三个部分，如下图所示：

1.5.2 代码

class Solution {
public:
    void quickSort(vector<int>& nums, int lo, int hi)
    {
        if (hi <= lo) return;
        int mid = nums[lo + hi + 1 >> 1];
        int i = lo - 1, j = hi + 1;

        while (i < j)
        {
            do i ++ ; while (nums[i] < mid);
            do j -- ; while (nums[j] > mid);
            if (i < j) swap(nums[i], nums[j]);
        }

        quickSort(nums, lo, i - 1);
        quickSort(nums, i, hi);
    }

    vector<int> sortArray(vector<int>& nums) {
        quickSort(nums, 0, nums.size() - 1);
        return nums;
    }
};

1.6 堆排序（优先队列）

1.6.1 实现思路

• 堆的原理是完全二叉树，但是可以用数组来进行模拟，小跟堆的堆顶存放最小元素。首先构造堆，从数组二分之一处往前遍历，对每个元素做下沉操作（比较堆顶与其左右子节点的大小，若堆顶元素更大，则与子节点交换位置），遍历完毕后整个堆就是有序的状态了。取出堆顶元素的操作可以视作：将堆顶元素与堆尾元素交换，堆大小减1（相当于抹除了最后一个元素），这时堆顶元素是最大的，将堆顶元素递归地做下沉操作，直到不能继续下沉为止，此时堆已经恢复到有序状态；

• 堆排序适用于TopK问题和多路归并问题，比如需要从十亿数据中取最大的十个，不需要对十亿规模的数据全部排序，只需要能存放10个元素的堆即可；

• 堆排序有下沉和上浮两种操作，排序只需要用下沉操作；

• 堆排序是唯一能够同时最优地利用空间和时间的方法——在最坏情况下也能保持2NlogN次比较和恒定的空间。它的代码实现简单，性能较好，但现代系统中却很少使用，因为它无法利用缓存：数组元素很少与相邻的元素进行比较，因此缓存未命中的次数要远高于大多数比较都在相邻元素间的排序算法，如快排、归并、希尔等。

1.6.2 代码

class Solution {
    vector<int> res, arr;
    int len;

public:
    void sink(int u)        //小跟堆的下沉操作，保持堆顶为最小元素
    {
        int t = u;

        //左儿子存在且左儿子小于父节点，则父节点下沉
        if (u * 2 <= len && arr[u * 2] < arr[t]) t = u * 2;
        //右儿子存在且右儿子小于父节点，则父节点下沉
        if (u * 2 + 1 <= len && arr[u * 2 + 1] < arr[t]) t = u * 2 + 1;

        if (u != t)                 //若 u == t 则表示当前节点已经无法下沉，这就是适合它的位置
        {
            swap(arr[u], arr[t]);
            sink(t);               //继续递归下沉，沉到不能沉为止
        }
    }

    vector<int> sortArray(vector<int>& nums) {
        int n = nums.size();
        len = n;

        //开了一个新数组，因为下标必须从1开始，从0开始的话，左子节点u * 2 = 0，就不是左子节点的下标了
        arr.resize(n + 1);
        for (int i = 1; i < arr.size(); ++ i)
        {
            arr[i] = nums[i - 1];
        }

        //最底部先垫一层，再插入，一边插入一遍排序。最底部一层元素数量为总元素的二分之一
        for (int i = n / 2; i > 0; -- i)
        {
            sink(i);
        }

        for (int i = 0; i < n; ++ i)
        {
            res.push_back(arr[1]);
            arr[1] = arr[len -- ];      //删除堆顶最小值
            sink(1);
        }

        return res;
    }
};

更新ing…