树的直径

$1.$ 无负权边

$Acwing1207$.大臣的旅费

两次$dfs$

证明:

$y$是距离$x$最远的一个点(第一次$dfs$得到)，假设$y$不是直径(最长路径)上的点(反证)
那么假设直径为$uv$
(1) $uv$和$xy$存在交点为$t$时

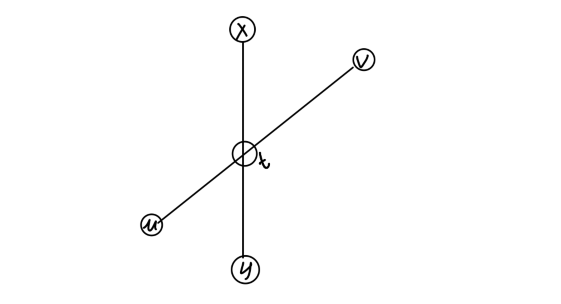
因为y为到x最远的点，所以$tv$≥$ty$，所以$vty$≥$vtu$，这与y不是直径上的点矛盾，所以y是直径上的点
(2) $uv$和$xy$不存在交点
因为图是树，所以这两条边之间一定存在相连的边，记为$pq$

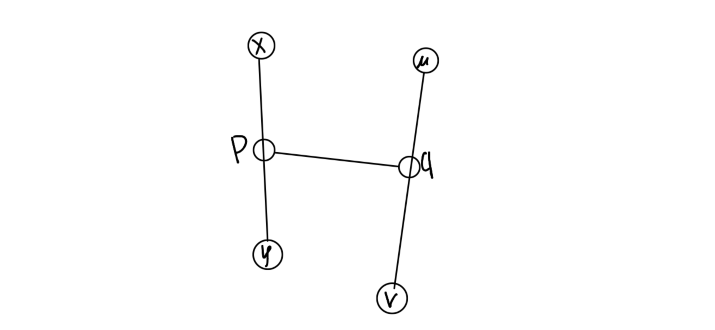
因为$y$为到$x$最远的点，所以$py≥pqv$，所以$uqpy≥uv$，这与$y$不是直径上的点矛盾，所以$y$是直径上的点

所以再用$y$来$dfs$一次即可树的直径

$2.$ 树中有负权边

因为有负权边，所以不能直接$dfs$求所有点之间的距离，但还是可以采用$spfa$，但$spfa$只能在$O(N^2)$时间复杂度内求出起点到终点的最短距离，并不能满足这里的求任意两点之间的最长路径要求，所以只能用树形$dp$来做。

$Acwing1072$.树的直径