A.购物单
用Excel
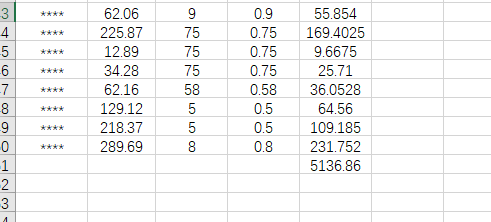
B.等差素数列
等差数列 An=A1+(n-1)*d
n为确定值,枚举A1,和d,d设个范围限制
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;
const int N=1e6+5;
typedef long long LL;
typedef pair<int,int> PII;
int p[N];
bool is_prime(int x)
{
if(x<2) return false;
for(int i=2; i<=x/i; i++)
if(x%i==0)
return false;
return true;
}
int main()
{
for(int x=2;; x++)
{
if(!is_prime(x)) continue;
for(int i=1; i<=500; i++)
{
cout<<"首项:" <<x;
cout<<"公差:"<<i<<" ";
int cnt=0;
for(int j=1; j<=9; j++)
{
int z=x+j*i;
if(!is_prime(z))
break;
else
{
cnt++;
cout<<z<<" ";
}
}
cout<<endl;
if(cnt==9)
{
cout<<"答案";
cout<<i<<endl;
return 0;
}
}
}
}
C.承重训练
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;
const int N=1e6+5;
typedef long long LL;
typedef pair<int,int> PII;
double a[35][35];
int main()
{
for(int i=1; i<=29; i++)
{
for(int j=1; j<=i; j++)
{
scanf("%lf",&a[i][j]);
}
}
for(int i=1; i<=29; i++)
{
for(int j=1; j<=i; j++)
{
double t=a[i][j]*0.5;
a[i+1][j]+=t;
a[i+1][j+1]+=t;
}
}
double min1=0x3f,max1=0;
for(int i=1;i<=30;i++)
{
min1=min(a[30][i],min1);
max1=max(a[30][i],max1);
}
LL sum=max1*(2086458231.0/min1);
cout<<sum<<endl;
}
D.方格分割
DFS板子
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;
const int N=1e6+5;
typedef long long LL;
typedef pair<int,int> PII;
int dir[][2]= {{1,0},{-1,0},{0,1},{0,-1}};
bool st[7][7];
int cnt;
void dfs(int x,int y)
{
//走到边界说明是一种方案,cnt++
if(x==0||y==0||x==6||y==6)
{
cnt++;
return ;
}
//dfs主体,向四个方向深入
for(int i=0; i<4; i++)
{
int nx=x+dir[i][0];
int ny=y+dir[i][1];
//走出地图或者走过了,不符合continue下一个
if(nx<0||nx>6||ny<0||ny>6||st[nx][ny]==true) continue;
//如果这点没有走过dfs该点
if(!st[nx][ny])
{
//对当前对进行标记,最后要恢复现场,回溯
st[nx][ny]=true;
//对对称点也进行标记(本题要求)
st[6-nx][6-ny]=true;
//dfs下去
dfs(nx,ny);
//回溯,恢复现场,开始时怎么样,结束时也要怎么样
st[nx][ny]=false;
st[6-nx][6-ny]=false;
}
}
}
int main()
{
st[3][3]=true;
//从中心开始向四周
dfs(3,3);
cout<<0.25*cnt<<endl;
}
E.取位数
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;
const int N=1e6+5;
typedef long long LL;
typedef pair<int,int> PII;
int len(int x)
{
if(x<10) return 1;
return len(x/10)+1;
}
int f(int x,int k)
{
if(len(x)-k==0) return x%10;
return f(x/10,k);
}
int main()
{
printf("%d\n",f(23574,3));
return 0;
}
F.最大公共子串
#include <stdio.h>
#include <string.h>
#include <iostream>
#define N 256
using namespace std;
int f(const char* s1, const char* s2)
{
int a[N][N];
int len1 = strlen(s1);
int len2 = strlen(s2);
int i,j;
memset(a,0,sizeof(int)*N*N);
int max = 0;
for(i=1; i<=len1; i++)
{
for(j=1; j<=len2; j++)
{
if(s1[i-1]==s2[j-1])
{
a[i][j] = a[i-1][j-1]+1;
if(a[i][j] > max) max = a[i][j];
}
}
}
return max;
}
int main()
{
printf("%d\n", f("abc", "efg"));
return 0;
}
G.日期问题
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <vector>
using namespace std;
const int N=4e4;
int days[13]= {0,31,28,31,30,31,30,31,31,30,31,30,31};
int cnt=0;
int ans[N];
int check(int date,int year,int month,int day)
{
if(month<=0||month>12||year<1960||year>2059) return 0;
int flag=((year%4==0&&year%100!=0)||year%400==0);
if(day>days[month]+flag||day<=0) return 0;
return date;
}
int main()
{
int a,b,c;
scanf("%d/%d/%d",&a,&b,&c);
//年份前面补19或20
int z=0;
//年月日
if(z=check(((1900+a)*100+b)*100+c,(1900+a),b,c)) ans[cnt++]=z;
if(z=check(((2000+a)*100+b)*100+c,(2000+a),b,c)) ans[cnt++]=z;
//日月年
if(z=check(((1900+c)*100+b)*100+a,(1900+c),b,a)) ans[cnt++]=z;
if(z=check(((2000+c)*100+b)*100+a,(2000+c),b,a)) ans[cnt++]=z;
//月日年
if(z=check(((1900+c)*100+a)*100+b,(1900+c),a,b)) ans[cnt++]=z;
if(z=check(((2000+c)*100+a)*100+b,(2000+c),a,b)) ans[cnt++]=z;
sort(ans,ans+cnt);
int count1=unique(ans,ans+cnt)-ans;
for(int i=0;i<count1;i++)
{
printf("%d-%02d-%02d\n",(ans[i]/10000),(ans[i]/100)%100,ans[i]%100);
}
return 0;
}
H.包子凑数
解题策略
1.先判断是否是INF的情况:
最大公因数等于 1 的时候,个数有限。 eg:(2,3,5)
最大公因数大于 1 的时候,个数无限。 eg:(2,4,6)
2.当求一个数(x)能否被这n个数(A1,A2,···,An)表示的时候,只需看 x-A1 || x-A2 ··· || x-An 能不能被表示出来
bool st[N];
st[i] = st[i - A1] || st[i - A2] ··· || st[i - An]
eg: 给定 3、4, 能否表示10:
-》判断 7(10 - 3)或 6(10 - 4)能否被表示 /*7可以,所以10能被表示*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <vector>
using namespace std;
const int N=1e5+5;
int n,sum;
int num[105];
bool st[N];
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
int main()
{
int d=0;
cin>>n;
for(int i=0; i<n; i++)
{
cin>>num[i];
st[num[i]]=1;
d=gcd(num[i],d);
}
if(d>1)
{
cout<<"INF"<<endl;
return 0;
}
for(int i=1; i<=N; i++)
{
for(int j=0; j<n; j++)
{
if(num[j]<i)
st[i]=(st[i]||st[i-num[j]]);
if(st[i]==true)
break;
}
}
for(int i=1; i<=N; i++)
{
if(!st[i]) sum++;
}
cout<<sum<<endl;
return 0;
}
I.分巧克力
骗样例
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <vector>
using namespace std;
const int N=1e5+5;
typedef pair<int,int> PII;
int n,k;
PII block[N];
int main()
{
scanf("%d %d",&n,&k);
for(int i=0;i<n;i++)
scanf("%d %d",&block[i].first,&block[i].second);
sort(block,block+n);
cout<<(int)(max(block[0].first,block[0].second)*0.5)<<endl;
}
J.K倍区间
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <vector>
using namespace std;
const int N=1e5+5;
typedef pair<int,int> PII;
int n,k,cnt,s;
int num[N];
int sum[N];
int main()
{
scanf("%d %d",&n,&k);
for(int i=1; i<=n; i++)
{
scanf("%d",&num[i]);
sum[i]=sum[i-1]+num[i];
}
for(int r=1;r<=n;r++)
{
for(int l=1;l<=r;l++)
{
s=sum[r]-sum[l-1];
if(s%k==0)
cnt++;
}
}
cout<<cnt<<endl;
}

