洛谷P1115最大子段和

原题链接 洛谷P1115最大子段和

如何用分治法求解最大子段和问题
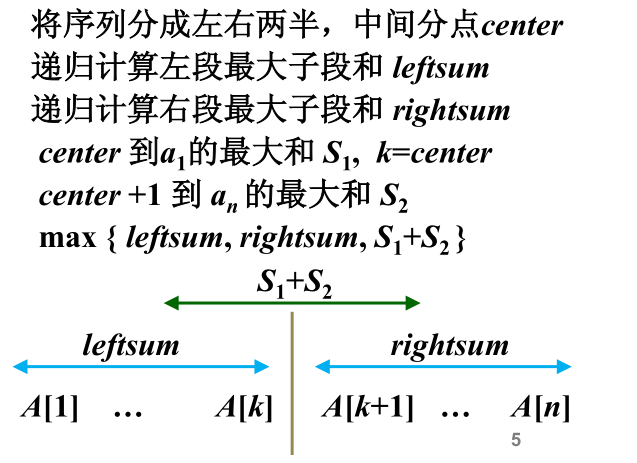
在数组的 center = (right-left)/2+left （中间）位置处分开。形成两个子数组。
那么，最大子段和 可能出现在三个位置：
a.可能出现在 左子数组
b.可能出现在 右子数组
c.可能出现在 过center的 中间某部分 元素 组成的子数组。
下面考虑 三种情况的计算方法：
第一种情况： 计算 left 到 center 的最大和(对应a)，记作 leftSum
第二种情况： 计算从 center+1 到 right的最大和(对应b)，记作 rightSum
第三种情况： 跨边界的和(对应c)。 以center为中心分别向两边计算和。
a.从 center出发，每次向左边扩张一步，并且记录当前的值S1，如果当前的和比上次的和大，就更新S1，一直向左扩张到位置 Left。
b.从 center+1出发，每次扩张一步，计算当前的和 为S2，如果当前的值比上次的和 大，那么，就更新S2的值，一直向右扩张到位置Right。
c.计算过center的连续值的和，S1+S2的值 Sum。 这个就是跨边界的和。
上面三种情况考虑计算完成后，最后一步就是，比较三个值中的最大值，取最大值就可以了。
时间复杂度为(nlogn)

屈婉玲教授讲解视频

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

const int N = 200010;

int n;
int arr[N];

const int minn = -1e10;

int maxSubSum(int l, int r)
{
    if (l == r) 
    {
        return arr[l];
    }
    int mid = (l + r) >> 1;
    int sum = 0, leftSum = minn, rightSum = minn; 
    for (int i = mid; i >= l; i--) 
    {
        sum += arr[i];
        if (sum > leftSum) leftSum = sum;
    }

    sum = 0;
    for (int i = mid + 1; i <= r; i++)
    {
        sum += arr[i];
        if (sum > rightSum) rightSum = sum;
    }
    return max(max(maxSubSum(l, mid), maxSubSum(mid + 1, r)), leftSum + rightSum);
}
int main()
{ 
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &arr[i]);
    }
    printf("%d\n", maxSubSum(1, n));
    return 0;
}