字符串题目占比相对比较少
一般会结合其他算法作为考点
一、匹配问题
符号
-
子串
1) 从原串中选取连续的一段,即为子串
2) 空串也是子串 -
前缀
pre(s, k)为 $s$ 前 $k$ 个字符构成的子串 -
后缀
suf(s, k)为 $s$ 后 $k$ 个字符构成的子串 -
任何子串都是某个后缀的前缀
- 最长公共前缀
lcp(s, t)
找出 $s$ 和 $t$ 最长的一样的前缀 -
最长公共后缀
lcs(s, t) -
周期
1) $0 < p < |p|$
2) $s[i] = s[i+p]$,$\forall \in \{1, 2, \cdots, |s|-p\}$
3) 满足以上条件,称 $p$ 为 $s$ 的周期 -
Border
1) $0 < p < |s|$
2) $pre(s, r) = suf(s, r)$
3) 满足以上条件,称 $pre(s, r)$ 是 $s$ 的border -
周期 与 Border
1) $3$ 和 $6$ 都是 $abcabcab$ 的周期
2) $abcab$ 和 $ab$ 都是 $abcabcab$ 的border
3) $pre(s, k)$ 是 $s$ 的 $border$ $\Leftrightarrow$ $|s| - k$ 是 $s$ 的周期
border 的传递性
- 串 $s$ 是 $t$ 的 $border$,串 $t$ 是 $r$ 的 $border$,那么 $s$ 是 $r$ 的 $border$
1) $aba$ 是 $ababa$ 的 $border$
2) $ababa$ 是 $abababa$ 的 $border$
3) 则有传递性:$aba$ 是 $abababa$ 的 $border$
border 更强的传递性
- 串 $s$ 是 $r$ 的 $border$,串 $t(|t| > |s|)$ 也是 $r$ 的 $border$,则 $s$ 是 $t$ 的 $border$
1) $aba$ 是 $abababa$ 的 $border$
2) $ababa$ 是 $abababa$ 的 $border$
3) 则 $aba$ 也是 $ababa$ 的 $border$ - 记 $mb(s)$ 表示 $s$ 的最长 $border$
1) 则 $mb(s), mb(mb(s)), \cdots$ 构成了 $s$ 的所有 $border$
2) $s$ 的所有 $border$ 环环相扣,被 $1$ 条链串起来
KMP
给定两个长度分别为 $n$ 和 $m$ 的串 $s$ 和 $t$,求 $t$ 在 $s$ 中出现的所有位置。
分析:
在 $t$ 的每个位置建立指针 fail[i],指向 $t[1 \cdots i]$ 的最长 $border$ (公共前后缀)。
怎么 $\rm{fail}[i]$ ?
从 $\rm{fail}[i-1]$ 开始,沿着 $\rm{fail}$ 指针走,直到下一位与 $t[i]$ 相同。
扫一遍 $s$,如果下一位与当前匹配的下一位不同,就沿着 $\rm{fail}$ 指针走。
时间复杂度:$O(n + m)$
$kmp$ 算法的动机:利用已经匹配的信息进行加速
例1: String Matching
给你一个目标串和模式串,要求统计出模式串在目标串中的出现次数
限制: $1 \leqslant n, m \leqslant 10^6$
C++ 代码
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::string;
using std::vector;
int main() {
string s, t;
cin >> s >> t;
int n = s.size(), m = t.size();
vector<int> fail(n);
fail[0] = -1;
for (int i = 1; i < m; ++i) {
int nxt = fail[i-1];
while (nxt != -1 and t[nxt+1] != t[i]) {
nxt = fail[nxt];
}
if (t[nxt+1] == t[i]) nxt++;
fail[i] = nxt;
}
int ans = 0;
for (int i = 0, j = -1; i < n; ++i) {
while (j != -1 and s[i] != t[j+1]) {
j = fail[j];
}
if (s[i] == t[j+1]) j++;
if (j == m-1) {
ans++;
j = fail[j];
}
}
cout << ans << '\n';
return 0;
}
例2: Finding Borders
给定字符串 $s$,找出 $s$ 的所有 $border$,并按从小到大的顺序输出这些 $border$ 的长度
限制: $1 \leqslant n \leqslant 10^6$
分析:
$s$ 的最长 $border$ 中包含 $s$ 的所有 $border$,所以只需处理出 $\rm{fail}$ 指针即可
C++ 代码
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::string;
using std::vector;
int main() {
string s;
cin >> s;
int n = s.size();
vector<int> fail(n);
fail[0] = -1;
for (int i = 1; i < n; ++i) {
int nxt = fail[i-1];
while (nxt != -1 and s[nxt+1] != s[i]) {
nxt = fail[nxt];
}
if (s[nxt+1] == s[i]) nxt++;
fail[i] = nxt;
}
for (int &x : fail) x++;
vector<int> ans;
int j = fail.back();
while (j) {
ans.push_back(j);
j = fail[j-1];
}
sort(ans.begin(), ans.end());
for (int x : ans) {
cout << x << ' ';
}
return 0;
}
例3: 【模板】KMP字符串匹配
C++ 代码
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::string;
using std::vector;
int main() {
cin.tie(nullptr) -> sync_with_stdio(false);
string s, p;
cin >> s >> p;
int n = s.size(), m = p.size();
vector<int> fail(m);
fail[0] = -1;
for (int i = 1; i < m; ++i) {
int nxt = fail[i-1];
while (nxt != -1 and p[nxt+1] != p[i]) nxt = fail[nxt];
if (p[nxt+1] == p[i]) nxt++;
fail[i] = nxt;
}
for (int i = 0, j = -1; i < n; ++i) {
while (j != -1 and s[i] != p[j+1]) j = fail[j];
if (s[i] == p[j+1]) j++;
if (j == m-1) {
cout << i-m+2 << '\n';
j = fail[j];
}
}
for (int x : fail) {
cout << x+1 << ' ';
}
return 0;
}
例4:Finding Periods
找出字符串 $s$ 的所有周期长度,并按升序输出
限制: $1 \leqslant n \leqslant 10^6$
C++ 代码
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::string;
using std::vector;
int main() {
string s;
cin >> s;
int n = s.size();
vector<int> fail(n);
fail[0] = -1;
for (int i = 1; i < n; ++i) {
int nxt = fail[i-1];
while (nxt != -1 and s[nxt+1] != s[i]) nxt = fail[nxt];
if (s[nxt+1] == s[i]) nxt++;
fail[i] = nxt;
}
for (int &x : fail) x++;
int j = fail.back();
while (j) {
cout << n-j << ' ';
j = fail[j-1];
}
cout << n << '\n';
return 0;
}
失配树(fail 树)
将 fail[i] 视为 $i$ 点的父节点,那么通过 fail 数组可以把 $0 \sim N$ 点连成一颗树,满足性质:
- 点 $i$ 的所有祖先都是前缀 $pre(s, i)$ 的 $border$
- 没有祖先关系的两个点 $i, j$ 没有 $border$ 关系
计算 fail[i] 的过程可以看做:从 j = fa[i-1] 开始不断往上走,找第一个不满足 s[j+1] = s[i] 的点,把 $i$ 点的父亲设为 $j+1$
例4. 动物园
先求出 fail[i] 数组,同时可以求出 cnt[i] 表示 pre(s, i) 的 $border$ 数量(包含自身)
易知 $cnt[i] = i$ 在失配树上的深度
令 $x[i] = pre(s, i)$ 不超过 $\frac{i}{2}$ 的最长 $border$ 长度
那么前缀 $pre(s, i)$ 的长度不超过 $\frac{i}{2}$ 的 $border$ 数量 $= cnt[x[i]]$
在失配树上倍增找 $x[i]$,$O(N\log N)$
性质:$x[i] \leqslant x[i-1] + 1$
- $x[i] - 1$ 需要是 $pre(s, i-1)$ 的 $border$
- $x[i] \leqslant \frac{i}{2}$,$x[i-1] \leqslant \frac{i-1}{2}$
- $x[i] - 1 \leqslant \frac{i}{2} - 1 \leqslant \frac{i-1}{2}$,且 $x[i-1]$ 是 $\leqslant \frac{i-1}{2}$ 的最长 $border$
x[i]取j = x[i-1]->0这条链上第一个满足s[j+1] = s[i]的 $j+1$- 类似 $KMP$ 的过程,$O(N)$
C++ 代码
#pragma GCC optimize ("O2")
#pragma GCC optimize ("unroll-loops")
#pragma GCC target ("avx2")
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::string;
using std::vector;
using std::istream;
using std::ostream;
using ll = long long;
//const int mod = 998244353;
const int mod = 1000000007;
struct mint {
ll x;
mint(ll x=0):x((x%mod+mod)%mod) {}
mint operator-() const {
return mint(-x);
}
mint& operator+=(const mint a) {
if ((x += a.x) >= mod) x -= mod;
return *this;
}
mint& operator-=(const mint a) {
if ((x += mod-a.x) >= mod) x -= mod;
return *this;
}
mint& operator*=(const mint a) {
(x *= a.x) %= mod;
return *this;
}
mint operator+(const mint a) const {
return mint(*this) += a;
}
mint operator-(const mint a) const {
return mint(*this) -= a;
}
mint operator*(const mint a) const {
return mint(*this) *= a;
}
mint pow(ll t) const {
if (!t) return 1;
mint a = pow(t>>1);
a *= a;
if (t&1) a *= *this;
return a;
}
// for prime mod
mint inv() const {
return pow(mod-2);
}
mint& operator/=(const mint a) {
return *this *= a.inv();
}
mint operator/(const mint a) const {
return mint(*this) /= a;
}
};
istream& operator>>(istream& is, mint& a) {
return is >> a.x;
}
ostream& operator<<(ostream& os, const mint& a) {
return os << a.x;
}
void solve() {
string s;
cin >> s;
int n = s.size();
vector<int> fail(n, -1);
vector<int> dep(n, 1);
for (int i = 1; i < n; ++i) {
int j = fail[i-1];
while (j != -1 and s[j+1] != s[i]) j = fail[j];
if (s[j+1] == s[i]) ++j;
fail[i] = j;
dep[i] = dep[j]+1;
}
mint ans = 1;
for (int i = 1, j = -1; i < n; ++i) {
while (j != -1 and s[j+1] != s[i]) j = fail[j];
if (s[j+1] == s[i]) ++j;
if (2*j >= i) j = fail[j];
ans *= dep[j]+1;
}
cout << ans << '\n';
}
int main() {
int t;
cin >> t;
while (t--) solve();
return 0;
}
例5. GT考试
用 dp[i][j] 来表示目前构造出来的串是 X[1...i],匹配到 $A$ 的第 $j$ 个字符
枚举第 $j+1$ 个数填 $k$
如果 $k$ 正好是 $A_{j+1}$,那么就会转移到 dp[i+1][j+1]
否则会转移到哪里呢?
沿着 fail[j], fail[fail[j]], ... 一直往回走,直到 A[fail[j]+1]=k
会转移到 fail[i+1][fail[j]+1]
可以发现 dp[i] 到 dp[i+1] 的转移可以看做左乘一个转移矩阵
我们只要算出这个矩阵的 $n$ 次幂,再乘上 dp[0] 就能得到我们想要的 dp[n] 了
时间复杂度:$O(m^3\log n)$
C++ 代码
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
using std::vector;
using std::string;
int mod;
vector<vector<int>> matmul(vector<vector<int>> A, vector<vector<int>> B) {
int n = A.size();
vector<vector<int>> C(n, vector<int>(n));
rep(i, n)rep(j, n)rep(k, n) {
C[i][k] += A[i][j] * B[j][k];
C[i][k] %= mod;
}
return C;
}
vector<vector<int>> matexp(vector<vector<int>> A, int b) {
int n = A.size();
vector<vector<int>> Z(n, vector<int>(n));
rep(i, n) Z[i][i] = 1;
while (b > 0) {
if (b & 1) Z = matmul(Z, A);
A = matmul(A, A);
b /= 2;
}
return Z;
}
int main() {
int n, m;
cin >> n >> m >> mod;
string s;
cin >> s;
s = '#' + s;
vector<int> fail(m+1);
for (int i = 2, j = 0; i <= m; ++i) {
while (j and s[j+1] != s[i]) j = fail[j];
if (s[j+1] == s[i]) ++j;
fail[i] = j;
}
vector A(m, vector<int>(m));
rep(i, m)rep(j, 10) {
int t = i;
while (t and s[t+1] - '0' != j) t = fail[t];
if (s[t+1] - '0' == j) ++t;
if (t != m) A[t][i]++;
}
A = matexp(A, n);
int ans = 0;
rep(i, m) {
ans += A[i][0];
ans %= mod;
}
cout << ans << '\n';
return 0;
}
Z 算法
Z 函数
对于一个字符串 $S$,和一个下标 $i(i > 1)$
令 $Z[i]$ 表示 $S$ 和 S[i...|S|] 的最长公共前缀
比如对于 $S = aabcaabxaaz$
${\color{Blue} {aab}} c{\color{Violet} {aab}} xaaz$ $Z[5] = 3$
${\color{Blue} a} abca{\color{Violet} a} bxaaz$ $Z[6] = 1$
$aabcaa{\color{Red} b} xaaz$ $Z[7] = 0$
$aabcaab{\color{Red} x} aaz$ $Z[8] = 0$
${\color{Blue} {aa}} bcaabx{\color{Violet} {aa}} z$ $Z[9] = 2$
Z box
对于任意的下标 $i > 1$ 且 $Z[i] > 0$
$Z \ box$ 就是 $[i, i+Z[i]-1]$ 这个区间
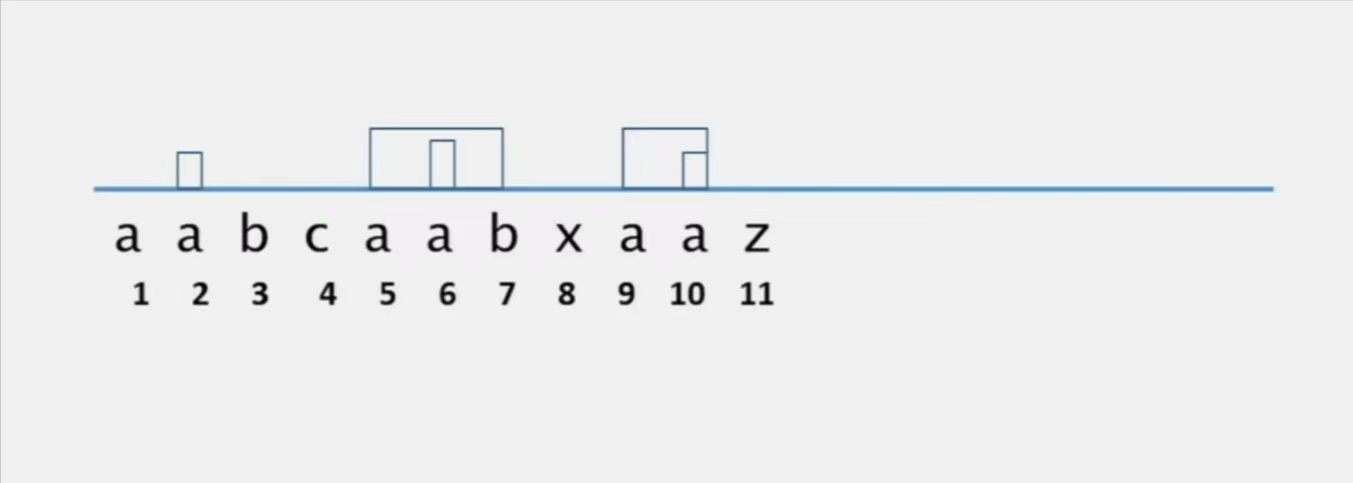
定义 $r[i]$ 为 $Z \ box$ 的右端点
$\alpha$ 为 $Z \ box$ 右端点在 $r[i]$ 的子串
$l[i]$ 为所有的 $\alpha$ 的左端点

$r[5] = 7$
$r[6] = 7$
$l[5] = 5$
$l[6] = 5$
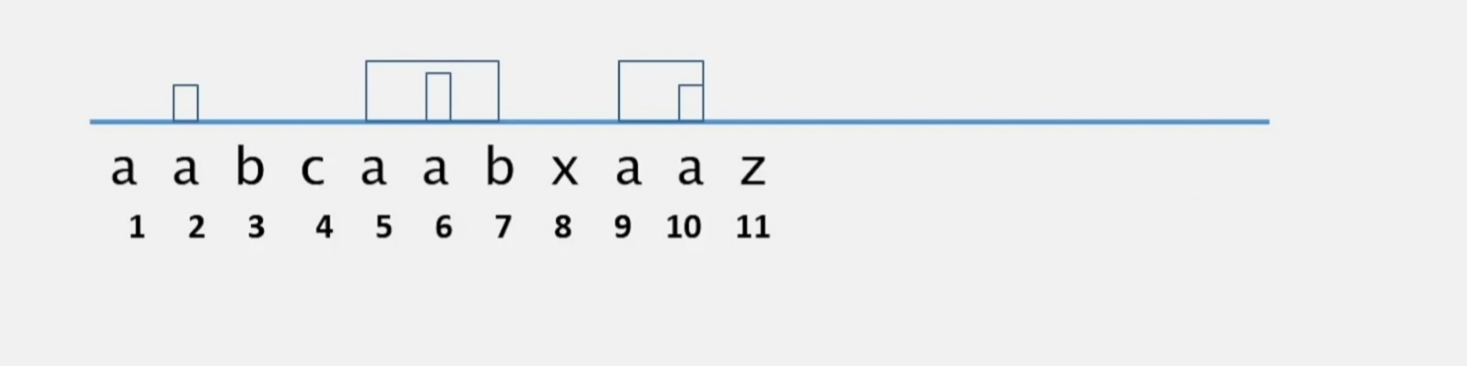
对于 $Z[2]$,我们需要暴力计算
也就是暴力计算 $S[1 \cdots |S|]$ 和 $S[2 \cdots |S|]$ 的最长公共前后缀
如果 $Z[2] > 0$,那么 $r = r[2] = 2 + Z[2] - 1$,$l = l[2] = 2$
如果 $Z[2] = 0$,那么 $r = r[2] = 0$,$l = l[2] = 0$
我们的目标就是用已有的 $Z[2], Z[3], \cdots, Z[k-1]$,来推出 $Z[k]$
假设 $k = 121$,$Z[2 \cdots 120]$ 已经知道了
$r[120] = 130$,$l[120] = 100$

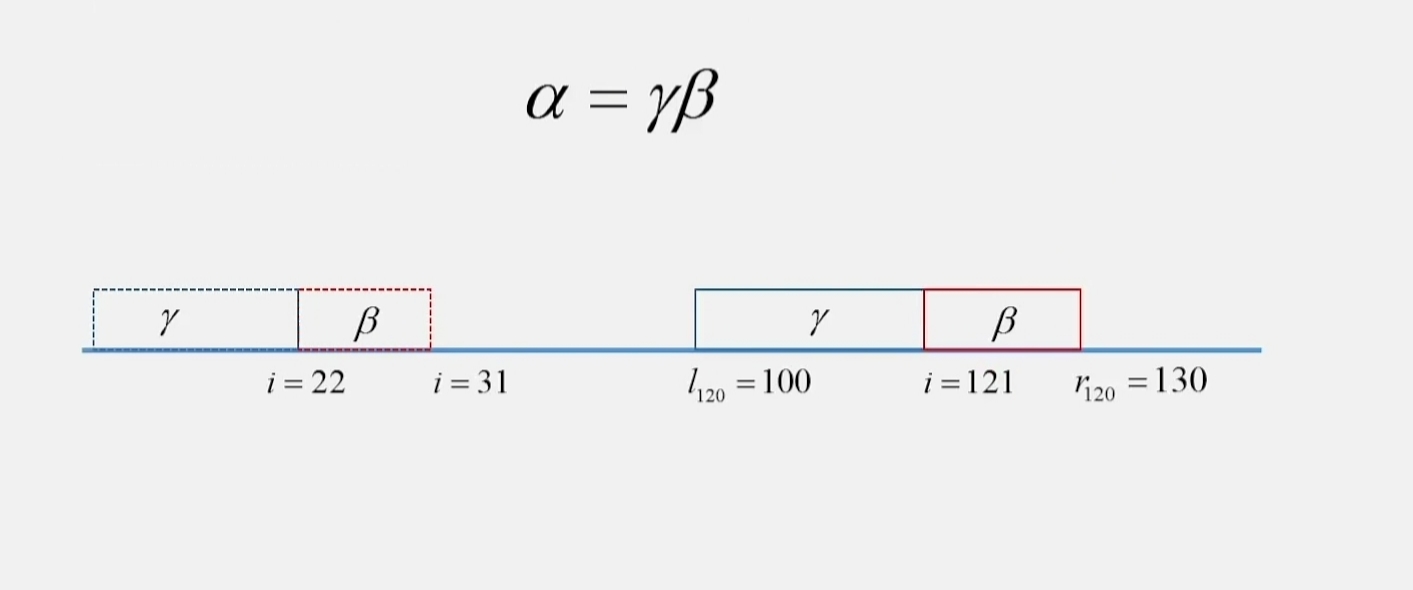
$\gamma = [l, i-1]$,$\beta = [i, r]$
$Z_{22} = 3$
$Z_{22} = 3 \Rightarrow Z_{121} = 3$

Case 1:$k > r$
这个时候没有 $\operatorname{Z-box}$ 可以利用,只能暴力计算 $Z[k]$
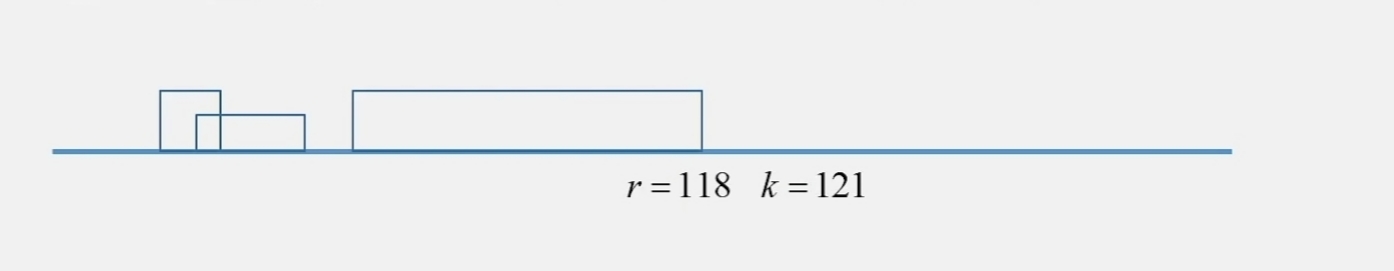
Case 2:$k \leqslant r$,$Z[k’] < |\beta|$, $k’$ 是前缀 $\beta$ 里的
这个时候 $Z[k]$ 就等于 $Z[i]$
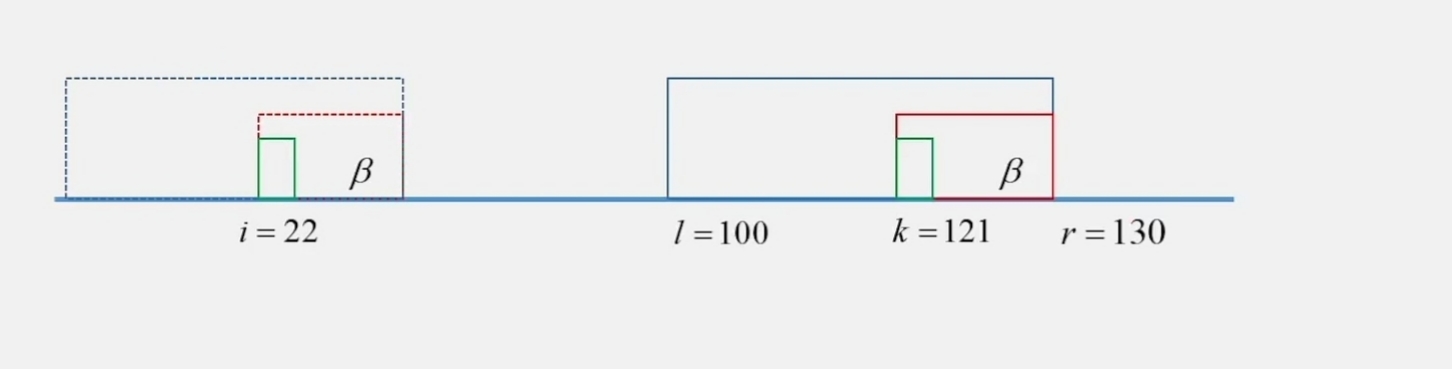
Case 3: $k \leqslant r$,$Z[k’] \geqslant |\beta|$
这时大于 $r$ 的部分还需要一个一个比较
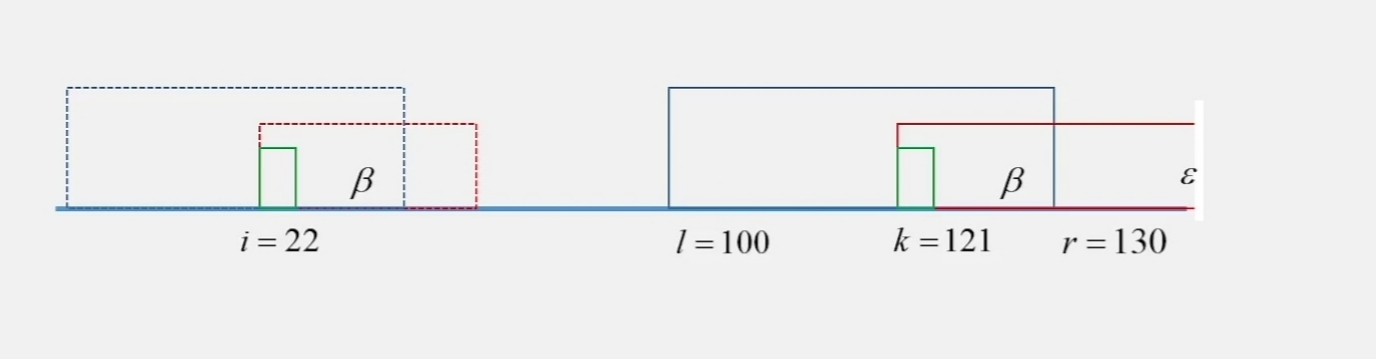
算法流程
计算完前 $i-1$ 个 $z$ 函数,维护盒子 $[l, r]$,则 $s[l, r] = s[1, r-l+1]$
1. 如果 $i \leqslant r$ (在盒内),则有 $s[i, r] = s[i-l+1, r-l+1]$
(1) 若 $z[i-l+1] < r-i+1$,则 $z[i] = z[i-l+1]$
(2) 若 $z[i-l+1] \geqslant r-i+1$,则令 $z[i] = r-i+1$,从 $r+1$ 后暴力枚举
2. 如果 $i > r$ (在盒外),则从 $i$ 开始暴力枚举
3. 求出 $z[i]$ 后,如果 $i+z[i]-1 > r$,则更新盒子 $l=i$,$r = i+z[i]-1$
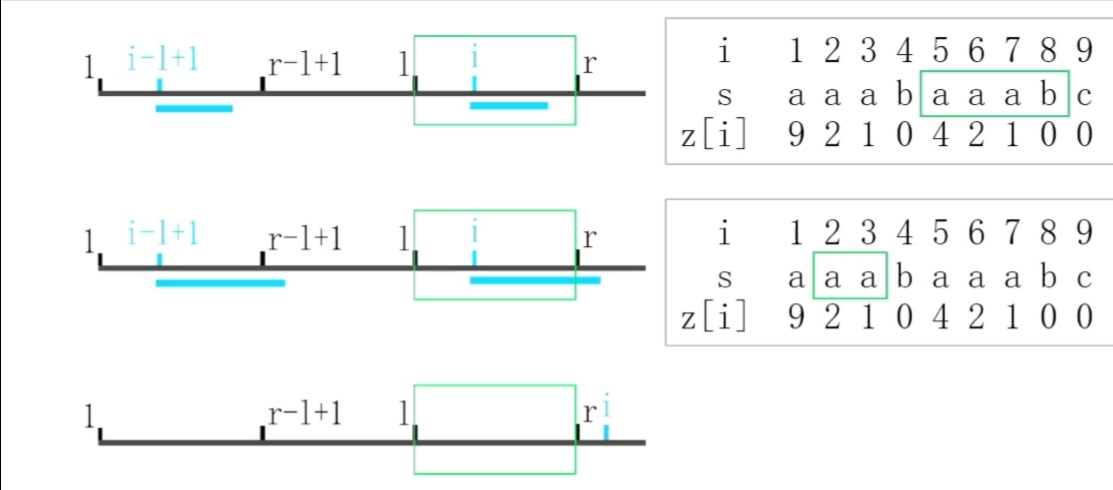
Z 算法时间复杂度分析
总共循环 $|S|$ 次,求出每一个 $Z[i]$
对于字符比较:
如果不相等,那么会终止循环。总共只会不相等 $|S|$ 次
如果相等,那么 $r$ 至少会加上 $r$。总共只会加 $|S|$ 次
因此时间复杂度是 $O(n)$ 的
代码实现
void get_z(char* s, int n) {
z[1] = n;
for (int i = 2, l, r = 0; i <= n; ++i) {
if (i <= r) z[i] = min(z[i-l+1], r-i+1);
while (s[1+z[i]] == s[i+z[i]]) z[i]++;
while (i+z[i]-1 > r) l = i, r = i+z[i]-1;
}
}
扩展 KMP 算法
给定两个字符串 $S$ 和 $T$(长度分别为 $n$ 和 $m$)
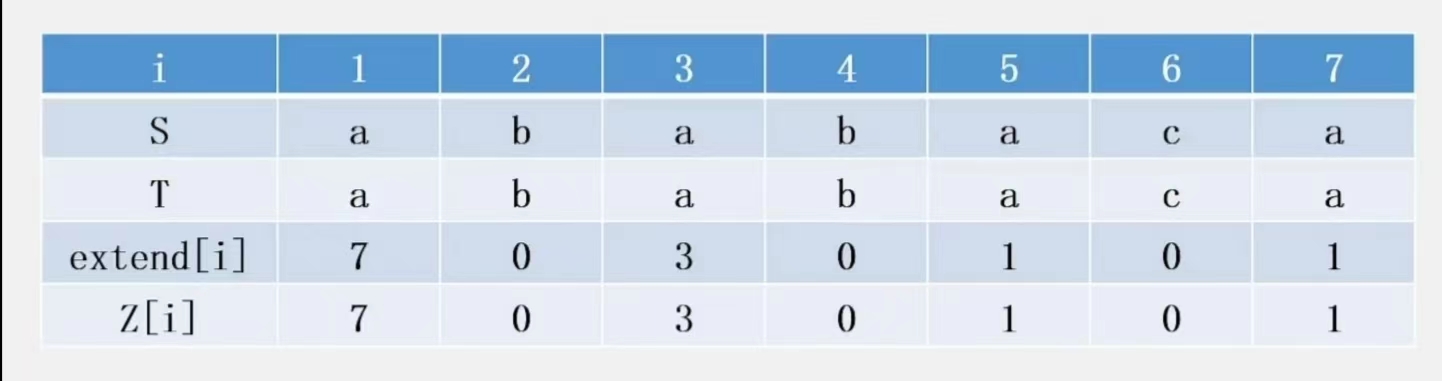
定义 extend[i] 为 $S[i \cdots n]$ 与 $T$ 的最长公共前缀的长度。
求出 $\operatorname{extend}$ 数组
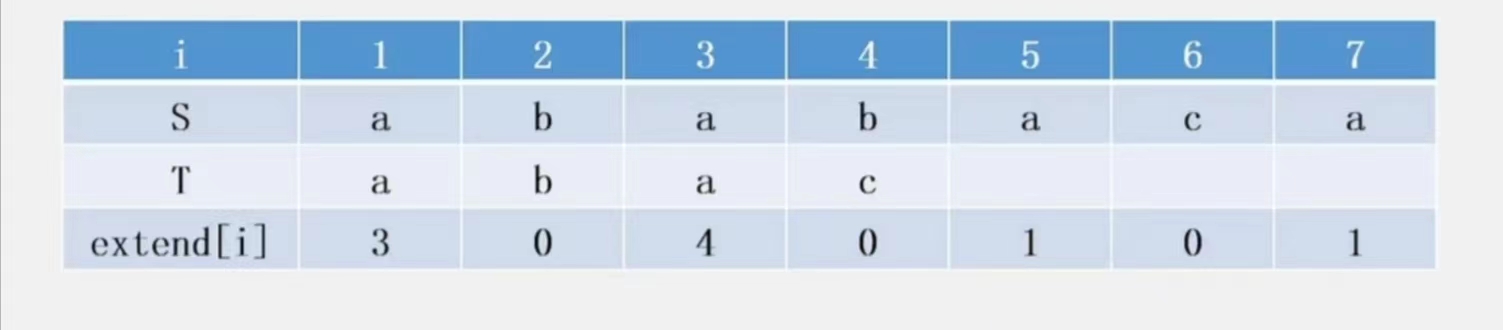
如果 $S=T$,那么 $\operatorname{extend}$ 数组就是 $Z$ 数组。
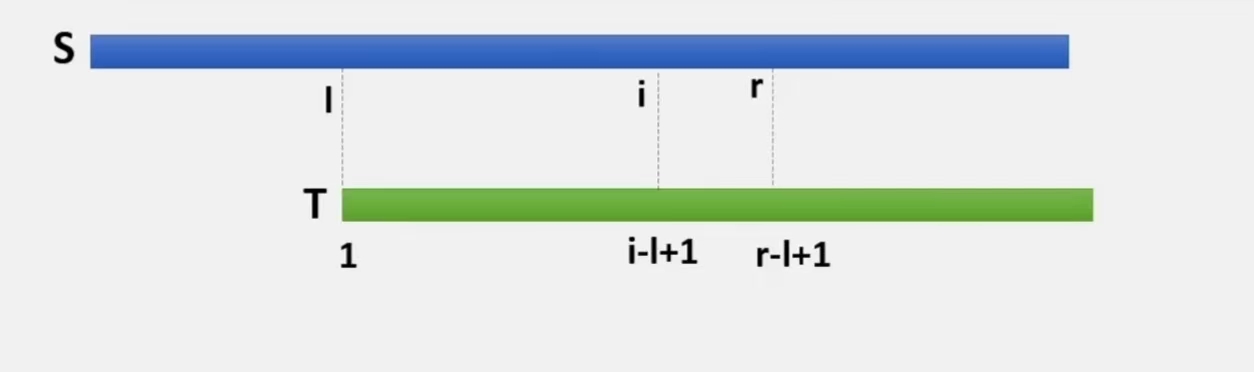
假设现在遍历到了 $S[i]$,且 $S[1], ~S[2], ~\cdots, ~S[i-1]$ 都已经算出
与 $Z$ 算法类似,设置两个变量 $l$ 和 $r$,$r$ 表示能和 $T$ 匹配到的最右边的位置,$l$ 为 $r$ 对应的起始位置
也就是 $S[l \cdots r] = T[1 \cdots r-l+1]$
$S[i]$ 对应的是 $T[i-l+1]$
现在要计算的是 $S[i \cdots n]$ 与 $T$ 的最长公共前缀
注意到此时 $S[i \cdots n] = T[i-l+1 \cdots r-l+1]$
所以我们可以先对 $T$ 求一遍 $Z$ 数组,然后考察一下 $Z[i-l+1]$
如果 $i+Z[i-l+1] - 1 < r$,extend[i] = Z[i-l+1]
如果 $i+Z[i-l+1] - 1 = r$
虽然 $T[r-l+2] \neq T[r-i+2]$,但是 $S[r+1]$ 可以等于 $T[r-i+2]$
我们可以 从 S[r+1] 与 T[r-i+2] 开始继续匹配
如果 $i+Z[i-l+1] - 1 > r$
说明 $S[i \cdots r]$ 与 $T[i-l+1 \cdots r-l+1]$ 相同
但是 $S[r+1] \neq T[r-l+2]$,且 $T[r-l+2] = T[r-i+2]$
所以 $S[r+1] \neq T[r-i+2]$,extend[i] = r-i+1
代码实现:
void calc_Z(char *s) {
int n = strlen(s+1);
for (int i = 1; i <= n; ++i) z[i] = 0;
z[1] = n;
int l = 0, r = 0;
for (int i = 2; i <= n; ++i) {
if (i > r) {
while (s[1+z[i]] == s[i+z[i]]) z[i]++;
l = i, r = i+z[i]-1;
}
else {
if (z[i-l+1] < r-i+1) z[i] = z[i-l+1];
else {
z[i] = r-i+1;
while (s[1+z[i]] == s[i+z[i]]) z[i]++;
l = i, r = i+z[i]-1;
}
}
}
}
void calc_extend(char *s, char *t) {
calc_Z(t);
int l, r = 0;
int n = strlen(s+1);
int m = strlen(t+1);
for (int i = 1; i <= n; ++i) {
if (i > r) {
while (i+ext[i] <= n and l+ext[i] <= m and s[i+ext[i]] == t[1+ext[i]]) ext[i]++;
l = i, r = i+ext[i]-1;
}
else {
if (i+z[i-l+1]-1 < r) ext[i] = z[i-l+1];
else {
ext[i] = r-i+1;
while (i+ext[i] <= n and 1+ext[i] <= m and s[i+ext[i]] == t[1+ext[i]]) ext[i]++;
l = i, r = i+ext[i]-1;
}
}
}
}

