位运算总结
在上文中 我们介绍了一些位运算的基础知识 我们此处来深入学习下异或内容
2022.5.8更新 将所有idx p初值初始化为1 极大情况可以避免边界问题
目录
1.异或性质 及例题
2.异或问题常见解决方式
3.异或前缀和及其应用
异或的性质
1、交换律
2、结合律 即(a ^ b) ^ c == a ^ (b ^ c)
3、对于任何数x 都有 x ^ x = 0 x ^ 0 = x
4、自反性: a ^ b ^ b = a ^ 0 = a
5. 对于任意的x 和 y 只要x != y 则 x ^ k != y ^ k(反证法可证)
例题 D1. 388535 (Easy Version)
题意
$\space\space\space\space\space$ 给定一组从0 -> n的所有数字异或x后的数组 让你求出任意一个可能的x值
分析
$\space\space\space\space\space$ 我们假设原数组为q[N] 异或后的数组为p[N] p[] q[]中任意两两不相同 根据性质4和5 因为p是q异或x后的数组 我们暴力枚举x 我们再对p进行一次异或->反转得到原数组 进而我们check 最大值是否就是原数组的最大值 && 最小值是否就是原数组的最小值即可(因为p中两两元素不相等 所以我们异或后的数也不会两两相等)进而对x进行判断 当然这种思路是常规思路 我们在该题的D2中判断 本题我们继续进行下分析
$\space\space\space\space\space$ 我们发现我们本题中的数组是从0开始 而不是任意一段 从0开始有什么特殊性呢？ 我们对n为8进行分析 (以下是二进制下的前8为数字)
000
001
010
011
100
101
110
111
$\space\space\space\space\space$因为我们的x是对每个数同一位进行异或 所以我们进行每一位上的数字观察发现 第一位(竖向) [01010101] 第二位[00110011] 第三位[00001111]我们发现 只要是从0开始的连续的数组 对所有数字的每一位分析 1的个数是 $\leq$ 0的个数 这是一个核心条件[原式数组q满足的性质 经过异或后p数组仅仅改变了某些位置01的个数 如果再次异或所形成的数组再次满足该性质 则x是一个可行解] 所以我们在求x的时候 我们只需要统计下每位上1和0的个数即可 如果该位上1的个数>0的个数 那么我们的x该位必须为1 进而使得该位上满足1的个数 $\leq$ 0 的个数即可
void solve()
{
for(int i = 0; i < 20; i ++) //初始化cnt数组
for(int j = 0; j < 2; j ++)
cnt[i][j] = 0;
cin >> l >> r;
for(int i = 0; i <= r; i ++)
{
cin >> q[i];
for(int j = 0; j < 20; j ++) cnt[j][(q[i] >> j) & 1] ++; //统计所有数 在同一个位数上0 1的个数
}
int sum = 0;
for(int i = 0; i < 20; i ++)
if(cnt[i][1] > cnt[i][0]) sum += 1 << i; //如果该位1的个数>0 的个数 我们需要进行异或置换操作
cout << sum << endl;
}
异或问题常见的解决方式
整形异或线性基 01异或trie
1.trie树
2.线性基
trie树
字典树 又称前缀树 是用于快速处理字符串的问题 能做到快速查找到一些字符串上的信息
另外 Trie树在实现高效的同时 会损耗更多的空间 所以Trie是一种以空间换时间的算法
Trie的思想
以下图片来源于 四谷夕雨
一 Trie的基本构造
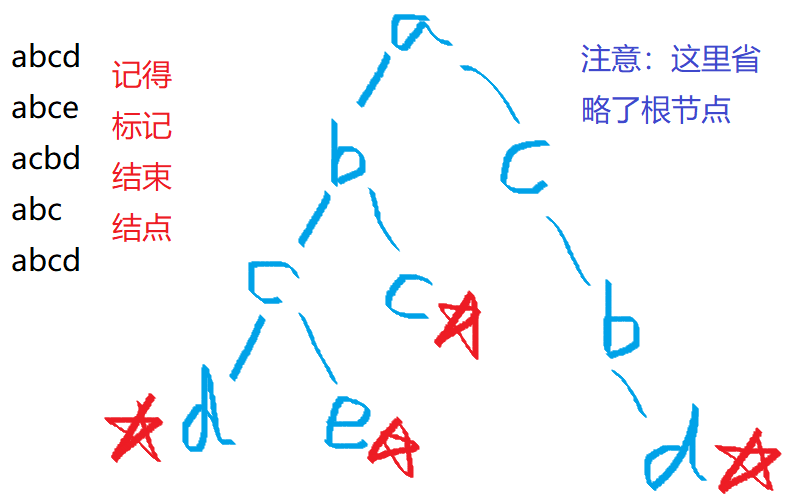
二 Trie的数组模拟
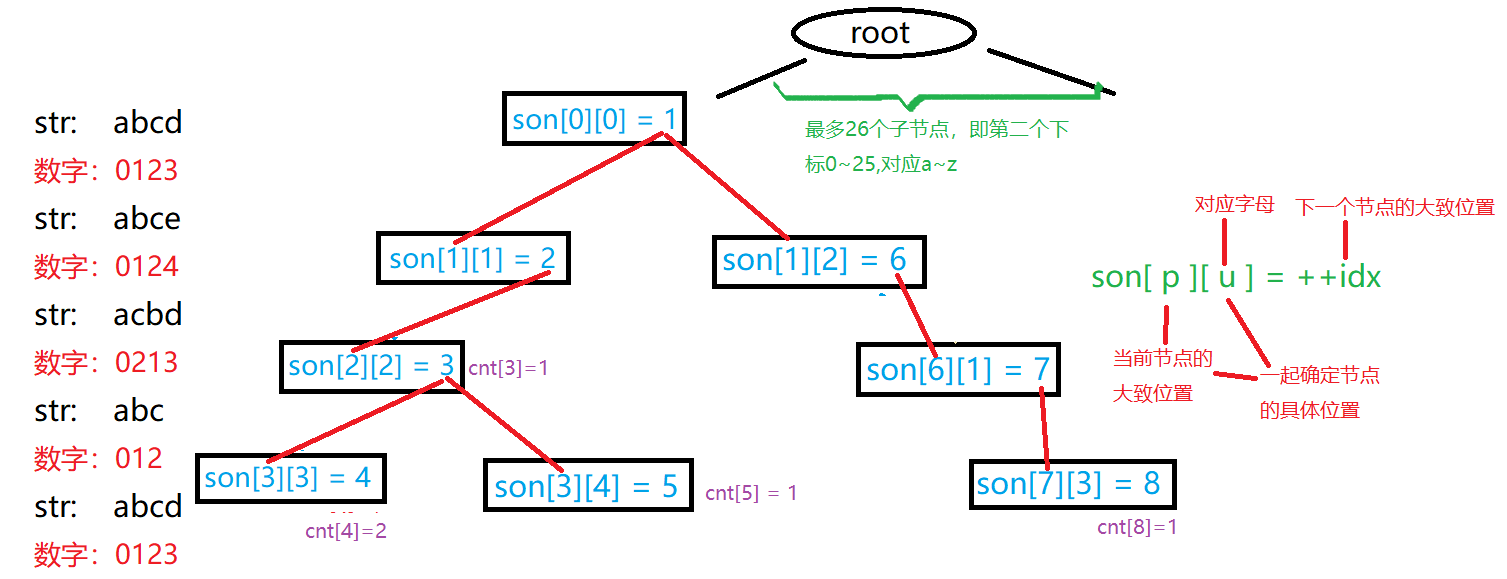
版本一
插入
int idx = 1;
void insert(char str[])
{
int p = 1; //指向当前节点
for(int i = 0; str[i]; i++)
{
int u = str[i] - 'a'; //将字母转化为数字
if(!son[p][u]) son[p][u] = ++idx;
//如果该节点不存在 则创建一个新的节点
p = son[p][u]; //更新p指针的信息
}
cnt[p]++; //结束的标记
}
查询
int query(char str[])
{
int p = 1;
for(int i = 0; str[i]; i++)
{
int u = str[i] - 'a';
if(!son[p][u]) return 0; //该节点不存在，即该字符串不存在
p = son[p][u];
}
return xxxxx; //看要求返回某些信息
}
版本二
插入
struct Node
{
int son[26];//记录儿子节点的所属个数
bool flag; // 标记是否为插入信息的末尾元素
}trie[N];
void insert(string s)
{
int p = 1;
for(int i = 0; s[i]; i ++)
{
int u = s[i] - 'a';
if(!trie[p].son[u]) trie[p].son[u] = ++ idx; //节点不存在 创造节点信息
p = trie[p].son[u]; //更新p的指针信息
}
trie[p].flag = true;//记录末尾元素信息
}
查询
int query(char str[])
{
int p = 1;
for(int i = 0; str[i]; i ++)
{
int u = s[i] - 'a';
if(!trie[p].son[u]) return res; //不存在则直接返回false
p = trie[p].son[u]; //更新指针信息
}
return xxxxxx; //看要求返回某些信息
}
ps 笔者较为推荐第二种写法 第二种在结构体中可以绑定多种信息便于查看 以下的所有代码均由第二种构造
例题分析
P2580 于是他错误的点名开始了
定义
struct Node{
int son[27],cnt; // son是儿子节点的选择 cnt是记录是否被念到货过
bool flag; //flag标记是否为末尾元素
}trie[N];
插入
void insert(string s){
int len = s.size(), p = 1; //获取长度len p是当前点的编号 根的编号是0
for(int i = 0; i < len; i ++)
{
int u = s[i] - 'a'; //获取位置
//如果没有继续下去的节点
if(!trie[p].son[u]) trie[p].son[u] = ++ idx; //就新建一个
p = trie[p].son[u]; //更新p指针信息
}
trie[p].flag=true; //标记此处是一个单词
}
查询操作
int query(string s)
{
int len = s.size(), p = 1;
for(int i = 0; i < len; i ++)
{
int p = s[i] - 'a'; //同上
if(!trie[p].son[u]) return 0; //找不到返回没有
p = trie[p].son[u]; //同上
}
if(trie[p].flag == false)return 0; //不是一个单词就返回没有
if(!trie[p].cnt)//如果没有被点过
{
//标记被点过了
trie[p].cnt ++;
return 1; //返回有
}
return 2; //不然返回重复
}
例题二 SP4033 PHONELST - Phone List
题意
$\space\space\space\space\space$给定一组字符串 判断有没有一个字符串是其他字符串的前缀 如果有就返回”NO” 没有返回”YES” 注意输出的坑
分析
$\space\space\space\space\space$ 如何快速判断一个字符串是另一个字符串的前缀?我们只需要对每个字符串的末尾元素判断是否存在子节点即可
// 定义
struct Node
{
int son[11], sum; //sum记录该点下面有几个儿子节点
void clear(){memset(son, 0, sizeof son); sum = 0;} //情况操作
}trie[N];
void insert(string str)
{
int p = 1;
for(int i = 0; str[i]; i ++)
{
int u = str[i] - '0';
if(!trie[p].son[u]) trie[p].son[u] = ++ idx;
trie[p].sum ++; //如果该点下有元素 我们先对该点的sum进行更新
p = trie[p].son[u];//更新当前点信息后 在跳转到下一个点
}
}
int serch(string str)
{
int p = 1;
for(int i = 0; str[i]; i ++)
{
int u = str[i] - '0';
if(!trie[p].son[u]) return 0;
p = trie[p].son[u];
}
if(trie[p].sum) return 1; //如果该点仍存在子节点 则是前缀
return 0;
}
例题三 最大异或对
Acwing原题 不在赘述
例题四 Secret Message G
题意
$\space\space\space\space\space$给定n个信息和m个暗号 统计每条暗号能够有多少个信息的前缀与其的前缀相同
分析
$\space\space\space\space\space$本题我们依旧类比与例题二的思路 不过与之不同的是 我们的前缀匹配也包含了暗号前缀 所以我们统计买个暗号的前缀匹配个数 加统计信息的前缀统计个数 根据容斥 在减去两者相同即两者相同的个数即可
struct Node
{
int son[2];
int cnt; // 记录在该点结束的有多少个
int sum;//经过该节点的路径
}trie[N];
void insert(string s)
{
int p = 1;
for(int i = 0; s[i]; i ++)
{
int u = s[i] - '0';
if(!trie[p].son[u]) trie[p].son[u] = ++ idx;
p = trie[p].son[u];
trie[p].sum ++; //经过该点的路径 ps与上一题的位置联想思考下 有何不同
}
trie[p].cnt ++; //在该点结束记录
}
int query(string s)
{
int p = 1;
int res = 0;
for(int i = 0; s[i]; i ++)
{
int u = s[i] - '0';
if(!trie[p].son[u]) return res;
p = trie[p].son[u];
res += trie[p].cnt;
}
return res + (trie[p].sum - trie[p].cnt); //记录经过每个点的所有信息 记得减去去重的完整路径
//ps 对于该式我们需要分析下 为何减少trie[p].cnt 我们的cnt是记录以该点结束的个数 //而sum则记录经过该点的路径 所以sum中包含了在该点结束的情况 所以去重
}
例题五 P4551 最长异或路径
题意
$\space\space\space\space\space$ 给定一棵 n个点的带权树，结点下标从 1 开始到 n寻找树中找两个结点，求最长的异或路径
分析
由异或的性质
结合律 即(a ^ b) ^ c == a ^ (b ^ c)
对于任何数x 都有 x ^ x = 0 x ^ 0 = x
自反性: a ^ b ^ b = a ^ 0 = a
所以本题中 sum(x, y)表示x -> y的异或和
Sum(X,Y)
= Sum(X,LCA) xor Sum(Y,LCA)
= Sum(X,LCA) xor Sum(Y,LCA) xor Sum(LCA,Root) xor Sum(LCA,Root)
= Sum(X,LCA) xor Sum(LCA,Root) xor Sum(Y,LCA) xor Sum(LCA,Root)
= Sum(X,Root) xor Sum(Y,Root)
$\space\space\space\space\space$所以我们需要预处理出所有的 root - > x的异或信息
void dfs(int x, int p) // 当前搜索x p是父节点
{
for(int i = h[x]; ~i; i = ne[i])
{
int k = e[i];
if(k != p) //往子节点的发向搜索
{
sum[k] = sum[x] ^ w[i]; //计算从根节点到该点的异或信息
dfs(k, x);
}
}
}
$\space\space\space\space\space$ 其次预处理好所有信息后 我们仅仅需要将其建树并跑一遍异或最大即可
void insert(int x)
{
int p = 1;
for(int i = 30; i >= 0; i --)
{
int u = x >> i & 1;
if(!trie[p].son[u]) trie[p].son[u] = ++ idx;
p = trie[p].son[u];
}
}
int query(int x)
{
int p = 1;
int sum = 0;
for(int i = 30; i >= 0; i --)
{
int u = x >> i & 1;
if(trie[p].son[!u])
{
sum += 1 << i;
p = trie[p].son[!u];
}
else p = trie[p].son[u];
}
return sum;
}
例题六 D2 - 388535 (Hard Version)
题意
$\space\space\space\space\space$还记得我们例题一的遗留问题吗 没错 在这呢
分析
$\space\space\space\space\space$我们只需要枚举x使得该数组的最小值等于原数组的最小值 最大值等于原数组的最大值即可 然而 真的就如此简单吗?显然这样我们铁T 所以我们需要优化下 我们考虑枚举(q[]原数组 p[]异或后题意给的数组)p[] ^ L 因为(L ^ X = P[], P[] ^ L = L ^ x ^ L = L) 所以我们枚举所有的P[] ^ L因为我们的L一定是来自q[]中 所以通过这样来进行对x的枚举 其次在枚举的时候 只要search_min(x) == L && search_max(x) == R即可判断成功
void init() //我们将初值都为1
{
son[1][0] = son[1][1] = 0;
idx = 1;
}
void insert(int x)
{
int p = 1;
for(int i = 30; i >= 0; i --)
{
int s = x >> i & 1;
if(!son[p][s])
{
son[idx + 1][0] = son[idx + 1][1] = 0; // 此处是对新开的点 idx处 初始化 而我们的idx 是++idx形式 所以也+ 1
son[p][s] = ++ idx;
}
p = son[p][s];
}
val[p] = x;
}
int search_max(int x)
{
int p = 1;
for(int i = 30; i >= 0; i --)
{
int s = (x >> i) & 1;
if(son[p][!s]) p = son[p][!s];
else p = son[p][s];
}
return val[p] ^ x; //切记 我们此时枚举的x 但 L ^ x = p[], p[] ^ x = L ^ x ^ x = L 所以此处返回异或x的值
}
int search_min(int x)
{
int p = 1;
for(int i = 30; i >= 0; i --)
{
int s = (x >> i) & 1;
if(son[p][s]) p = son[p][s];
else p = son[p][!s];
}
return val[p] ^ x; //同上
}
void solve()
{
init();
cin >> L >> R;
for(int i = L; i <= R; i ++)
{
cin >> a[i];
insert(a[i]);
}
for(int i = L; i <= R; i ++)
{
int x = a[i] ^ L;
if(search_min(x) == L && search_max(x) == R)
{
cout << x << endl;
break;
}
}
}
例题七 E. Beautiful Subarrays
题意
$\space\space\space\space\space$ 给定一个数组q 以及一个k值 求数组的q中区间异或 $\geq$ k的区间个数
分析
$\space\space\space\space\space$ 因为是区间异或 且由异或性质可知 s[r] ^ s[l-1] = s[l -> r] 所以我们可以考虑对区间异或前缀和进行建树 有了异或前缀和 即转化为我们对于1 ~ n 中的每个 i 求以第i的数结尾的区间异或和大于等于k的有多少 即s[0 . . i - 1] 中有多少个与 s[i]异或大于等于k 然后我们跑异或最大计算即可
源码
//本题define int long long 卡空间
typedef long long LL;
#define endl '\n'
const int N = 1e6 + 5;
int n, m;
int now;
int idx = 1;
LL ans;
struct Node
{
int son[2];
long long sum;
}trie[N * 31];
LL query(int x)
{
int p = 1;
LL ans = 0;
for(int i = 30; i >= 0; i --)
{
int u = x >> i & 1;
int v = m >> i & 1;
if(v) p = trie[p].son[!u];// 如果v该位为1 表示 我们必须得走到u点异或为1 的点
else
{
ans += trie[trie[p].son[!u]].sum; //记录该点异或为1的情况
p = trie[p].son[u];//并继续走另一边
}
}
ans += trie[p].sum; //记录等于的情况
return ans;
}
void insert(int x)
{
int p = 1;
for(int i = 30; i >= 0; i --)
{
int u = x >> i & 1;
if(!trie[p].son[u]) trie[p].son[u] = ++ idx;
p = trie[p].son[u];
trie[p].sum ++;
}
}
void solve()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++)//前缀异或和 我们对 s[1 ^ 2 ^...^ n] 判断 前面的值有多少异或大于
{
int x;
cin >> x;
insert(now);
now ^= x;
ans += query(now);
}
cout << ans << endl;
}
线性基
太累了 鸽一会 (我不会告诉你其实我还没学会)
异或前缀和
太累了 鸽一会 (这是真的)
