K.贪心
基础知识
1.含义:
①很贪婪:找最优解
②很短视:只会看重眼前的局面不会往后想
2.题目特点:
①跳跃性很强:没有固定的模型,所有贪心题基本上没有什么共性
②可能代码很短,但结论证明很难
3.解题策略:
①找相似
考试的时候看一下这道题跟平时做的有没有相似的,然后套一下相似题目的做法
所以平时多积累归纳总结不同的贪心模型
②猜
考试实在不会就只能猜了,一般贪心题的虽然策略证明很麻烦,但代码都很短,一般可能就是按照按照某个关键字排个序,然后从小到大处理一遍就可以了。
4.一些话:
①贪心题一般都是先猜然后再去证明正确性
②很多贪心问题都可以转换成数学模型,是因为出题人根据数学模型加了些背景出了这些贪心题
例题
一、股票买卖II
1.策略:
(策略就是做法)
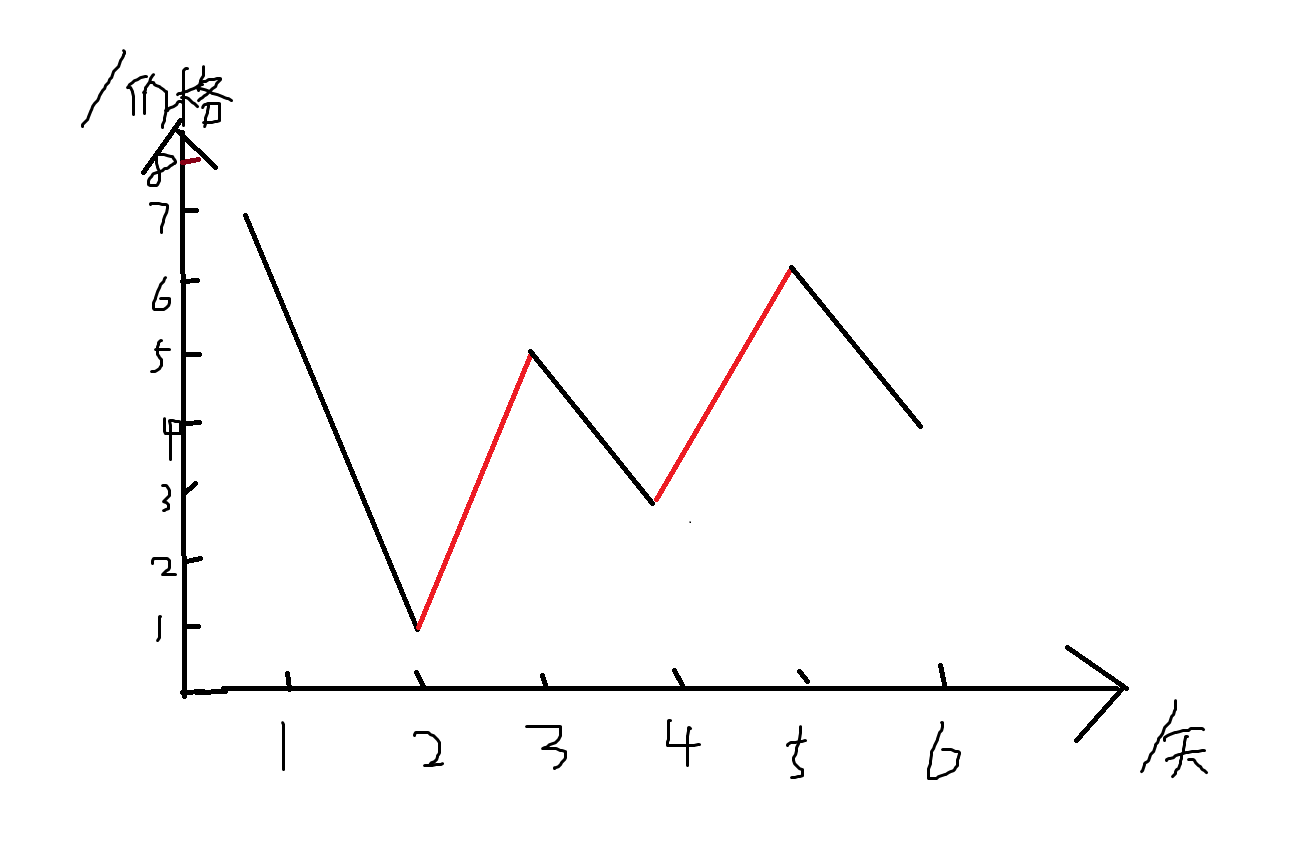
遇增则买:依次看相邻两天,只要后一天价格大于前一天的价格,则交易一次,加起他们之间的差值
2.证明:
性质:任何跨度大于一天的交易都可以拆分成若干个跨度等于一天的交易
所以可以独立的看只要每一段上升的全部都加起来
3.代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int price[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &price[i]); //输入比较长,推荐使用scanf
int res = 0;
for (int i = 0; i + 1 < n; i ++ ) //依次遍历所有跨度为1的交易
{
int dt = price[i + 1] - price[i]; //算交易
if (dt > 0)//只要交易是正的,统计加起来
res += dt;
}
printf("%d\n", res);
return 0;
}
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int a[100010]; //注意题目数据范围
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
int sum=0;
for(int i=1;i<=n;i++)
{
if(a[i]<a[i+1])
sum+=(a[i+1]-a[i]);
}
cout<<sum;
return 0;
}
4.总结:
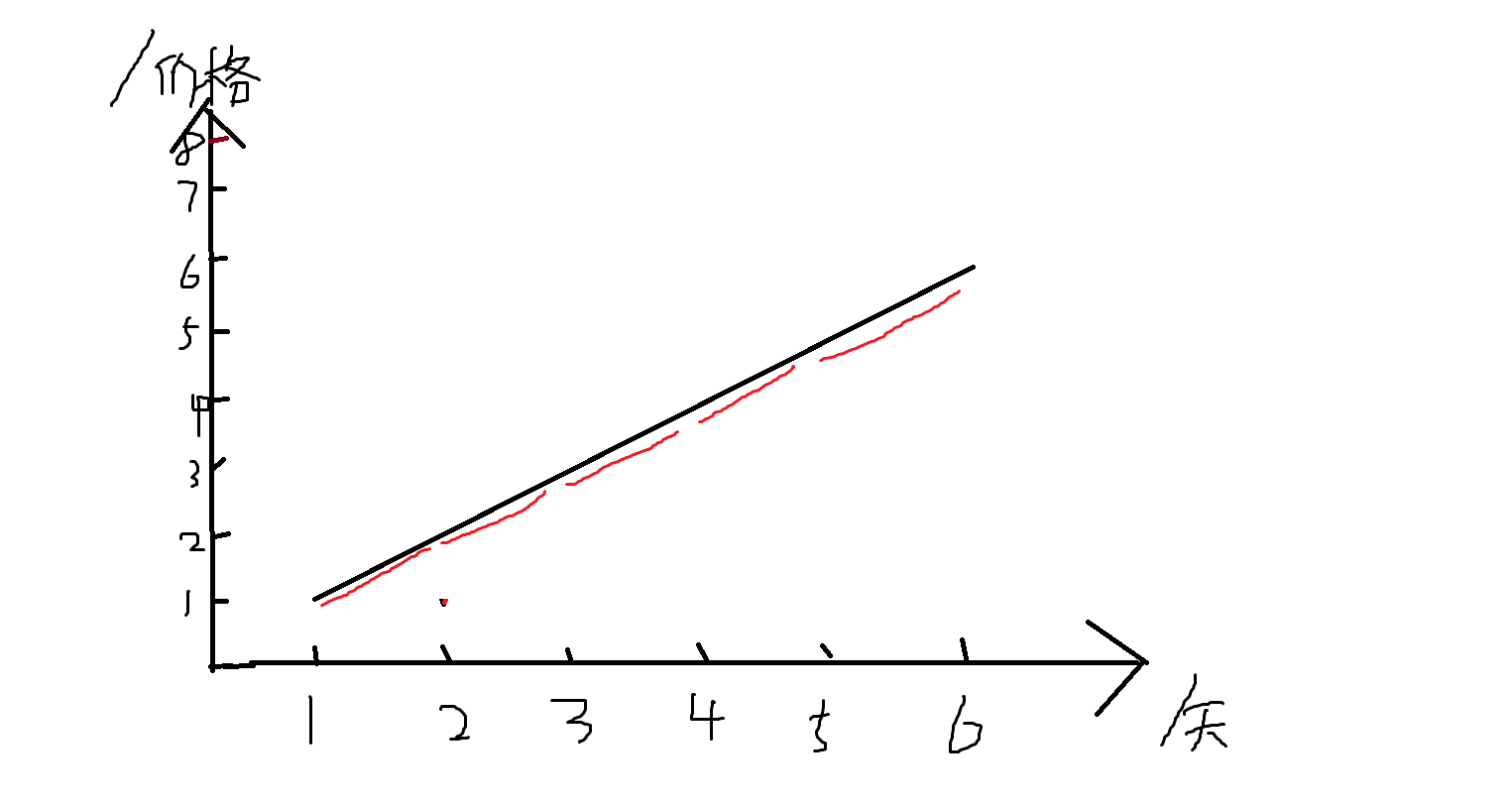
一开始思路:可以从数学坐标轴去理解找到这道题解法,在折线图中,可以发现交易时一定是上升的折线,所以只需要找到拐点,即该点小于两边的点和该点大于两端的点,然后求和算出每段上升折线这两段一小一大两个点的差值即可。代码实现时还要注意特判一下整个两端的边界,分多种情况讨论。
后来发现上述的性质,其实每一段上升的折线都可以分成若干个相邻天数之间的上升端,所以就简单了,直接找比前一个大的小段即可。
二、货仓选址
1.策略:
排序+中位数
①奇数个商店:在中位数
②偶数个商店:中间两个数之间都可
注意:这两个可以合并,偶数个商店时,在中间两个数之间任意点都可,包括这两个点。不管奇数个商店,还是偶数个商店,直接选取中间靠右端点就包括这两种情况。(如果选用中间靠左端点,奇数个时还需单独讨论)。又因为C++中的/是向下取整,所以
当下标从0开始时,mid=a[n/2]
当下标从1开始时,mid=a[n/2+1]
2.证明:
可以发现这个问题可以用数学公式表示,然后利用分组通过几何意义来求解这个公式

(很多贪心问题都可以转换成数学模型,是因为出题人根据数学模型加了些背景出了这些贪心题)
3.代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010;
int n;
int x[N]; //用x表示坐标
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &x[i]); //输入所有的坐标
sort(x, x + n);//依次给所有的坐标排序
int c = x[n / 2]; //求出商店的位置在中点,c++中的/是向下取整
LL res = 0; //注意会不会爆int,用longlong存保险
for (int i = 0; i < n; i ++ ) res += abs(x[i] - c); //求一下到中点的距离
printf("%lld\n", res);
return 0;
}
//奇数偶数个时分开看
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
const int N=100010;
int a[N];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1);
int mid;
if(n%2!=0)
mid=a[n/2+1];
else
mid=a[n/2];
int sum=0;
for(int i=1;i<=n;i++)
{
sum+=abs(mid-a[i]);
}
cout<<sum;
return 0;
}
//下标从1开始时合并奇偶数做法
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
const int N=100010;
int a[N];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1);
int mid=a[n/2+1];
int sum=0;
for(int i=1;i<=n;i++)
{
sum+=abs(mid-a[i]);
}
cout<<sum;
return 0;
}
//下标从0开始时合并奇偶数的做法
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
const int N=100010;
int a[N];
int n;
int main()
{
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
sort(a,a+n);
int mid=a[n/2];
int sum=0;
for(int i=0;i<n;i++)
{
sum+=abs(mid-a[i]);
}
cout<<sum;
return 0;
}
三、糖果传递
1.策略:
前缀和减去平均数+货仓选址
①计算出原数组的前缀和数组减去平均值之后的数组
②对得到数组进行排序
③累加求出每个点到中位数的距离之和(转换为货仓选址)
2.证明:
证明过程借鉴了这位大佬的题解AcWing 122. 糖果传递 - AcWing
3.代码:
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;//注意输入数据的范围
const int N=1000010;
int n;
ll a[N];
ll x[N];
int main()
{
cin>>n;
ll sum=0;
//输入原数组,求出平均值
for(int i=1;i<=n;i++)
{
cin>>a[i];
sum+=a[i];
}
ll ave=sum/n;
//求出前缀和数组减去平均值
for(int i=1;i<=n;i++)
{
x[i]=x[i-1]+a[i]-ave;
}
//对得到数组排序
sort(x+1,x+n+1);
//累加求出每个点到中位数的距离之和(转换为货仓选址贪心模型)
ll mid=x[n/2+1];
ll cnt=0;
for(int i=1;i<=n;i++)
{
cnt+=abs(mid-x[i]);
}
cout<<cnt;
return 0;
}
四、雷达设备
1.策略:
思路:转化为区间合并问题
该题可转换为给定 n个区间,在 xx轴上选择尽量少的点,使得所有区间至少包含一个点。
(1)将所有区间按右端点从小到大排序;
(2)依次考虑每个区间:
①如果当前区间包含最后一个选择的点,则直接跳过;
②如果当前区间不包含最后一个选择的点,则在当前区间的右端点的位置选一个新的点;
2.证明:
参考题解:AcWing 112. 雷达设备 - AcWing
3.代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 1010;
int n, d;
struct Segment
{
double l, r;
bool operator< (const Segment& t) const
{
return r < t.r;
}
}seg[N];
int main()
{
scanf("%d%d", &n, &d);
bool failed = false;
for (int i = 0; i < n; i ++ )
{
int x, y;
scanf("%d%d", &x, &y);
if (y > d) failed = true;
else
{
double len = sqrt(d * d - y * y);
seg[i].l = x - len, seg[i].r = x + len;
}
}
if (failed)
{
puts("-1");
}
else
{
sort(seg, seg + n);
int cnt = 0;
double last = -1e20;
for (int i = 0; i < n; i ++ )
if (last < seg[i].l)
{
cnt ++ ;
last = seg[i].r;
}
printf("%d\n", cnt);
}
return 0;
}
五、付费问题
1.策略:
首先我们要知道标准差表示的是数据与平均值之间的波动程度,其值越大波动越大。要使得标准差小,我们就要尽可能使得数据都比较接近平均值。
那么这题贪心策略应该是这样的:
(1)首先算出平均值s/ns/n,
(2)把数据从小到大排序,
(3)每个同学看看能不能负担得起,如果最少的人负担不起,那么就有多少负多少,否则的话就所有人平摊,一直循环到所有人平摊为止
①如果某个人的钱低于该值,那么他一定是将钱全部支付,
②然后其余不够的其他人平摊。但是,由于之前那个人钱不够,那么就会导致剩下人支付的平均值会增大,所以在这个平摊过程中很有可能存在某个人钱又低于这个平均值,又需要剩下的人平摊。如此反复,直到支付完成。
2.证明:
实质上是一个均值不等式问题
参考这位大佬的题解AcWing 1235. 付账问题 - AcWing
3.代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 500010;
int n;
int a[N];
int main()
{
long double s;
cin >> n >> s; //读入总人数和总共需要掏的钱数
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
sort(a, a + n);
long double res = 0, avg = s / n; //res存的是方差,最后再开一个根号得到标准差
//avg为平均值
//double会出过不掉最后一个数据的,要用long double
for (int i = 0; i < n; i ++ )
{
double cur = s / (n - i); //算一下当前每个同学需要均摊的钱是多少
if (a[i] < cur) cur = a[i]; //如果当前的同学的钱数小于要均摊的钱的话,那么他的钱数要全部支付
//否则的话,他要交的钱就是代均摊的钱
res += (cur - avg) * (cur - avg); //求方差
s -= cur; //总钱数减去上缴的钱,表示已经支付的这么多钱了
}
printf("%.4Lf\n", sqrt(res / n)); //输出标准差
return 0;
}
六、乘积最大
1.解题思路:
可以最终将方法归纳为一个贪心+双指针算法:
- 将序列从小到大排序,这样有三种排列的可能:
1)序列中有正数有负数:绝对值大的数在两端,左端为负数绝对值大的,右端为正数绝对值大的,绝对值小的数在中间
2)序列中全是正数:绝对值大的在右端,绝对值小的在左端
3)序列中全是负数:绝对值大的在左端,绝对值小的在右端
-
如果k是奇数,那么先把最右边的数取了,它可能是最大的正数,也可能是绝对值最小的负数(对应所有数都是负数的情况)(但是无论哪种情况,这么取都是能保证最后的结果最大的,如果序列中至少存在一个正数,最后结果为正数,想要结果的绝对值最大,那么它一开始就把最大的数取了;如果序列中都是负数,最后的结果为负数,想要结果的绝对值最小,那么它一开始取的是绝对值最小的负数,也保证了最后负数的绝对值最小,即负数的最大值),然后问题转化为在n−1个数里面选k−1个数,因为k−1为偶数,那么问题转化为情况1了
-
如果k是偶数,那么属于情况1,只需要在排好序的序列两端,成对的取更大的数对即可
算法的实现思路是贪心,实现方法是双指针
本质上考察分类讨论算法:
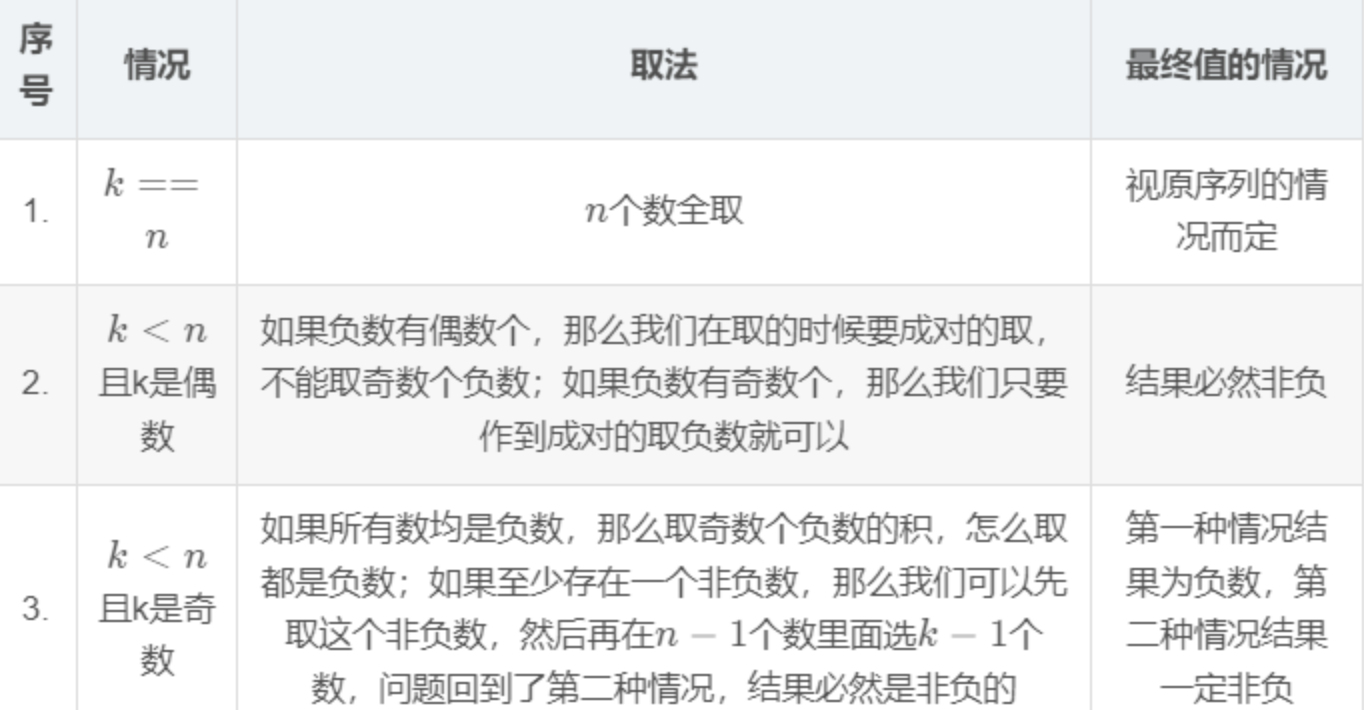
2.注意:
细节问题:题目中说在C中,对负数取模的结果就是负数,比如−8%5=−3,题目这里也即交代了C本来就有的性质,故而不需要特殊处理。
3.代码:
/*
首先我们知道 如果 k == n ,那么就证明所有的数字是全部都选,
如果 k < n , 那么就要思考怎样去选择了:
1.k 如果是偶数的话,选出来的结果一定是非负数 , 原因如下:
(1) # 负数的个数是偶数个的话,负负得正,那么一定是非负数
(2) # 负数的个数如果是奇数个的话,那么我们就只选偶数个绝对值最大的负数
2.k 如果是奇数个的话,
(1)# 所有的数字如果都是负数,那么选出来的结果也一定都是负数
(2)# 否则的话,则一定至少有 1个非负数, 那么我们将最大的数取出来, 此时要选的个数就是 k--,
# k-- 是偶数,那么就又转化为 k-- 是偶数的情况思考
*/
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long LL ;
const int N = 100010 , mod = 1000000009 ;
int a[N];
int main()
{
int n , k ;
scanf("%d%d",&n,&k);
for(int i = 0 ; i < n ; i ++) scanf("%d",&a[i]);
sort(a,a + n);
LL res = 1 ; //乘积初始化
int l = 0 , r = n - 1 ;//双指针初始化
int sign = 1 ; // 符号初始化
//由于4种情况除了 k 是奇数且 k < n 的时候需要特判一下处理一下符号 ,其他的时候都可以转化为双指针做法
//k 是奇数是先选出最大的数, k-- 就是偶数,两边再同时取对,转化成相同的双指针做法
if(k % 2 )
{
res = a[r]; // 取出最大的一个数
r -- ; //右指针移动
k -- ; //个数减1
if(res < 0) sign = -1; // 如果最大值都是负数,就证明全是负数,那么符号要发生改变
}
while(k) // 双指针做法
{
LL x = (LL)a[l] * a[l + 1] , y = (LL)a[r] * a[r - 1];//两边同时取对
//选择更大的一对,和归并排序思路相近
if(x * sign > y * sign)
{
res = x % mod * res % mod; // 需要注意的是 :不可以写成(x * res) % mod ,也不可以写成是 res % mod * x % mod
// 因为x最大是 10^10,如果不先取模的话,和res相乘的结果最大是 10^19,会暴long long。
l += 2; // 指针移动
}
else
{
res = y % mod * res % mod;
r -= 2;
}
k -= 2;
}
printf("%lld",res);
return 0;
}
参考题解:https://www.acwing.com/solution/content/8724/
七、后缀表达式
1.解题思路:
首先明白这道题为什么叫后缀表达式,后缀表达式转为中缀表达式,相当于加括号,实际后缀表达式没有括号,中缀表达式可以有括号。因为后缀表达式不再引用括号(其实是隐式的引用括号),比如2 3 + 1 - 这个式子,就是(2+3)−1=4, 从左向右计算,不考虑括号,运算符放在两个运算对象之后。
因为符号和数字的顺序可以随便安排,那么可以考虑下面几种情况:
- 如果都是加号:那么直接将所有的数字全部加起来即可
- 如果有一个减号,那么我们可以转化为 …+…−(....+....+…) 的形式,即分为两部分,中间一个减号,因此只要出现一个减号那么就可以视为出现一个或多个减号等同的效果。
- 如果出现多个减号:也可以转化为…+…−(....+....−…)的形式,也就是说你希望它是减号时你可以把它放到括号外,你希望它是加号时,你可以把它放在括号里边,因为负负得正,因此,一个减号与多个减号可以视作一种情况。
总结一下就是:只要m>0, 那么减号的数量实际上就是1 到n+m的任何一个数字。
因此得到下列讨论结果:
- 如果全是加号,答案就是所有数字直接相加。
- 如果存在减号:
- 如果全是正数,那么至少有一个被减去,所以把最小的那个减去即可。
- 如果有正有负,那么所有正数匹配正号,所有负数匹配负号,因此将它们的绝对值直接相加
- 如果全是负数,那么除了维持一个最大的负数(因为负数越大它的绝对值越小)为负数之后外,其他的全部翻正
通俗来说:

如果没有负号,就直接算所有数的和。
如果有负号,把所有数排个序,最大的拿出来,放首项,把最小的数拿出来,给他一个减号,再套一个括号。
把加号都给负数放到括号里面,把减号给正数变成负数再放到括号里面,如果有多出来的加号给正数放到括号外面,如果有多出来得减号给负数放到括号外面。
2.代码:
/*
其实就是-号可以通过 -负数转成+号,最终就是等同于最大数减去最小数 再加上剩余所有数的绝对值
最关键一点:要分析出来负号的个数其实可以任选1~m+n都可以。因为可以通过加括号的方式可以构造出来任意多个负号。
代码思路:
1)先特判if(m==0)的话,直接算所有数的和。
2)否则,if(m>0)的话,
经过分析,至少要减一个数,要加一个数
所以找到最小值和最大值,减去最小值,加上最大值。除了最大值和最小值之外的中间所有数,可以任给他一个符号,如果是正数就给他正号,负数就给他符号,即取中间各数的绝对值。
*/
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 200010;
int n, m;
int a[N];
int main()
{
scanf("%d%d", &n, &m);
int k = n + m + 1;
for (int i = 0; i < k; i ++ ) scanf("%d", &a[i]);
LL res = 0;
if (!m)
{
for (int i = 0; i < k; i ++ ) res += a[i];
}
else
{
sort(a, a + k); // 也可以不排序,找出最大值和最小值即可
res = a[k - 1] - a[0];
for (int i = 1; i < k - 1; i ++ ) res += abs(a[i]);
}
printf("%lld\n", res);
return 0;
}
参考题解:https://www.acwing.com/solution/content/8491/
八、灵能传输
1.解题思路:
参考题解:https://www.acwing.com/solution/content/97431/
2.代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 300010;
int n;
LL a[N], s[N];
bool st[N];
int main()
{
int T;
scanf("%d", &T);
while (T -- )
{
scanf("%d", &n);
s[0] = 0;
for (int i = 1; i <= n; i ++ )
{
scanf("%lld", &a[i]);
s[i] = s[i - 1] + a[i];
}
LL s0 = s[0], sn = s[n];
if (s0 > sn) swap(s0, sn);
sort(s, s + n + 1);
for (int i = 0; i <= n; i ++ )
if (s[i] == s0)
{
s0 = i;
break;
}
for (int i = n; i >= 0; i -- )
if (s[i] == sn)
{
sn = i;
break;
}
memset(st, 0, sizeof st);
int l = 0, r = n;
for (int i = s0; i >= 0; i -= 2)
{
a[l ++ ] = s[i];
st[i] = true;
}
for (int i = sn; i <= n; i += 2)
{
a[r -- ] = s[i];
st[i] = true;
}
for (int i = 0; i <= n; i ++ )
if (!st[i])
a[l ++ ] = s[i];
LL res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, abs(a[i] - a[i - 1]));
printf("%lld\n", res);
}
return 0;
}
CSDN链接: https://blog.csdn.net/qq_46009744/article/details/123894141?spm=1001.2014.3001.5501

