1. 背包体积最多$m$

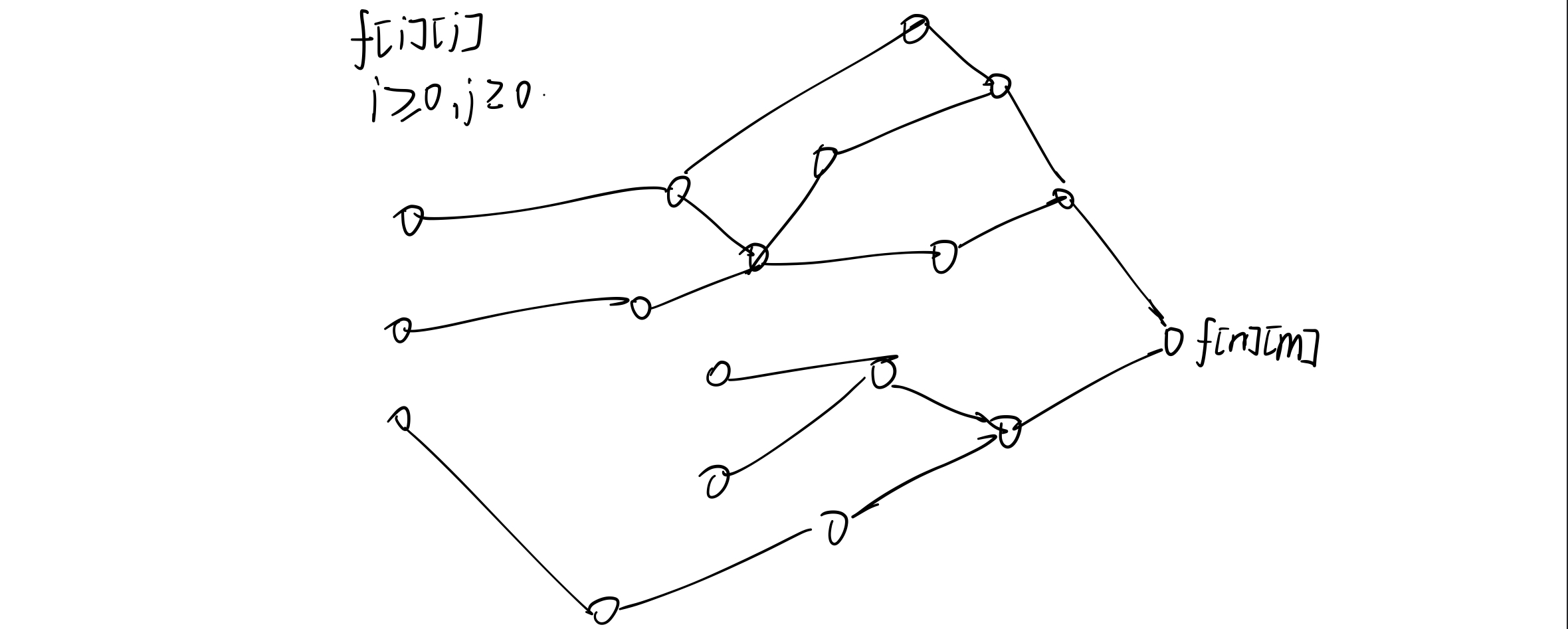
体积最多$m$的求解拓扑图是一个多起点单终点的拓扑图，起点可以是多种体积

2. 背包体积恰好$m$

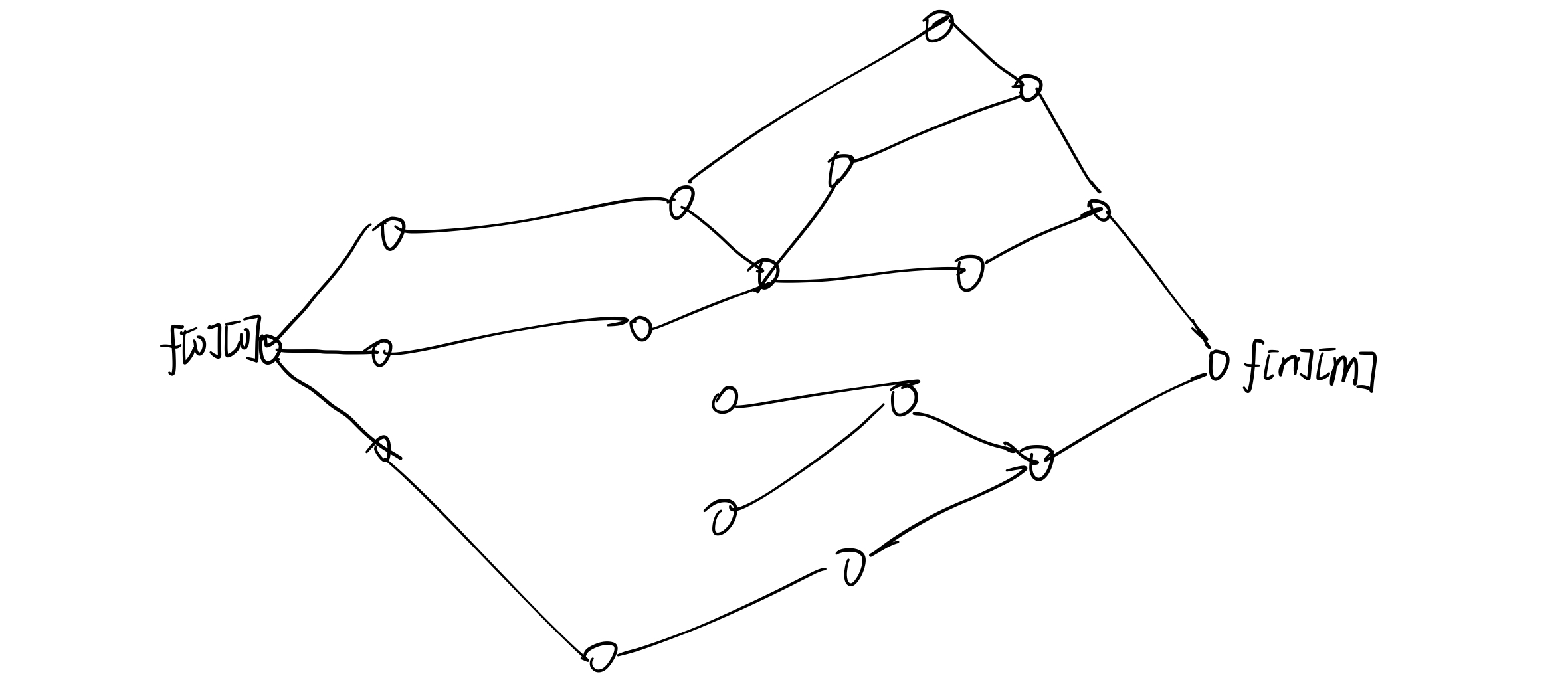
体积恰好$m$的求解拓扑图是起点只能为$f[0][0]$，终点$f[n][m]$

① 恰好装满时求最大值

初始化： $memset$($f$, $-INF$, $sizeof$ $f$); $f[0][0]= 0$;
状态转移：$f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i])$
如果求解结束后$f[n][m]=-INF$,则无法满足恰好将体积装满。

② 恰好装满时求最小值

初始化： $memset$($f$, $INF$, $sizeof$ $f$); $f[0][0]= 0$;
状态转移：$f[i][j] = min(f[i][j], f[i-1][j-v[i]]+w[i])$
如果求解结束后$f[n][m]=INF$,则无法满足恰好将体积装满。

3. 背包体积至少$m$

体积至少$m$的求解拓扑图是一个”多起点”单终点的拓扑图，这个”多起点”是因为可以从负体积转移过来，选第一件物品的时候可以由负体积转移过来，比如$f[1][20]$，可以选一个体积为$30$的物品(从$f[0][-10]$转移过来)，因为体积要求是至少$20$。所以其实也是一个单起点$f[0][0]$问题

① 至少装满$m$求最大值

初始化： $memset$($f$, $-INF$, $sizeof$ $f$); $f[0][0]= 0$;
状态转移：$f[i][j] = max(f[i][j], f[i-1][max(j-v[i],0)]+w[i])$
因为是至少装满，所以只要所有物品加起来可以满足体积最小要求，一定是有解的

① 至少装满$m$求最小值

初始化： $memset$($f$, $INF$, $sizeof$ $f$); $f[0][0]= 0$;
状态转移：$f[i][j] = min(f[i][j], f[i-1][max(j-v[i],0)]+w[i])$
因为是至少装满，所以只要所有物品加起来可以满足体积最小要求，一定是有解的