预备知识

n为点的个数，m为边的个数
稀疏图：m与n为一个量级
稠密图：m与$n^2$为一个量级

建图的两个方法，
邻接矩阵（用于稠密图）

g[n][n]存点a到点b的距离。首先要初始化为 正无穷，其中g[a][a]=0

邻接表（用于稀疏图）

int h[m],e[m],ne[m],idx,w[m];
初始化，idx=0；memset(h,-1,sizeof h);
//存图操作,存的是边
add(int a,int b,int c)
{
   e[idx]=b;
   w[idx]=c;
   ne[idx]=h[a];
   h[a]=idx++;

}
//遍历单链表操作
for(int i=h[a];i!=-1;i=ne[i])
{
    int j=e[i];
}

一些特殊图：
无向图：无向图为特殊的有向图，存图的时候双向建边即可。即g[a][b]=g[b][a]
重边：对于两个点，有多条边，在最短路问题里，记录最短的那条边即可,（邻接表无须特判）
负环：存在负环可能无最短路
（若负环在所求最短路两点之间，负环可以无限次走，距离为负无穷）
（若负环不在所求最短路两点之间，负环对其不造成影响）

最短路问题

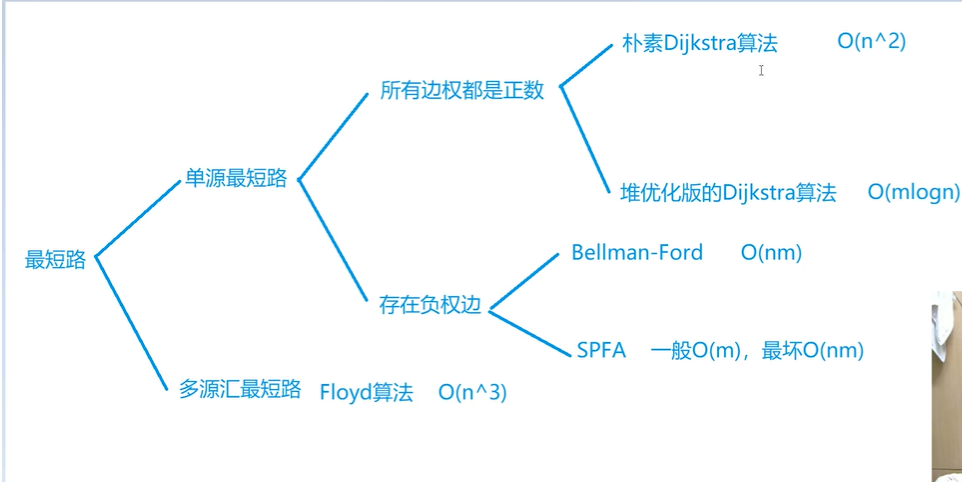
最小生成树问题
定义：对一堆点，找一堆边可以将所有点联通起来。
当一堆边的权值累加最小时，这堆边称为最小生成树

注意最小生成树问题都是无向边

稀疏图一般用krsual，稠密图用朴素版prim，堆优化版本很少用到，可以被krusal代替