树的直径

$\color{red}{一、定义：树上最远两点（叶子结点）的距离。}$

求树的直径

从树上任意点u开始DFS(BFS)遍历图，得到距离u最远的结点v,然后从v点开始DFS遍历图，得到距离v最远的结点w， 则v、w之间的距离就是树的直径。

例题：1207. 大臣的旅费
https://www.acwing.com/problem/content/description/1209/

#include <iostream>
#include <cstring>

using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
int n;
int h[N], e[N], w[N], ne[N], idx;
LL dist[N];
bool st[N];
LL maxson, maxd;
void add(int a, int b, int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx ++;
}

void dfs(int x)
{
    st[x] = true;
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int a = e[i], b = w[i];
        if (st[a]) continue;
        dist[a] = dist[x] + b;
        if (maxd < dist[a]) maxd = dist[a], maxson = a;
        dfs(a);
    }
}

int main()
{
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    for (int i = 1; i < n; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
        add(b, a, c);
    }

    dfs(1);
    memset(dist, 0, sizeof dist);
    memset(st, false, sizeof st);
    maxd = 0;
    // cout << maxson << endl;
    dfs(maxson);
    // cout << dist[3] << endl;
    LL t = (21 + maxd) * maxd / 2;
    printf("%lld\n",t);
    return 0;
}

$\color{red}{二、性质：树上任意点能到的最远点，一定是树的直径的某个端点。}$

求树上每个节点到达的最大距离

先求出树的直径，然后从直径的两个端点u和v分别DFS整棵树，对于每个结点得到两个距离d[i].u和d[i].v， 二者的最大值即是i点能到的最远点的距离。
例题：computer
http://acm.hdu.edu.cn/showproblem.php?pid=2196

二叉树的先序遍历、中序遍历、后序遍历

$\color{red}{先序遍历：}$

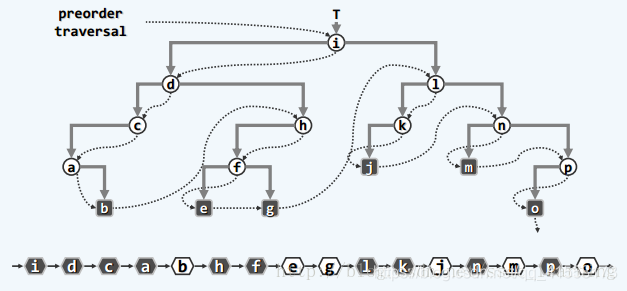
遍历:

void trav_mid_tree(tree* x)//后序遍历
{
    if (x == NULL) return;
    cout << x->val << ' ';
    trav_mid_tree(x->left);
    trav_mid_tree(x->right);
}

$\color{red}{中序遍历：}$

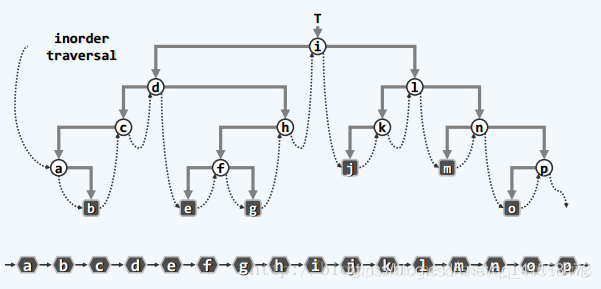
遍历:

void trav_mid_tree(tree* x)//中序遍历
{
    if (x == NULL) return;
    trav_mid_tree(x->left);
    cout << x->val << ' ';
    trav_mid_tree(x->right);
}

$\color{red}{后序遍历：}$

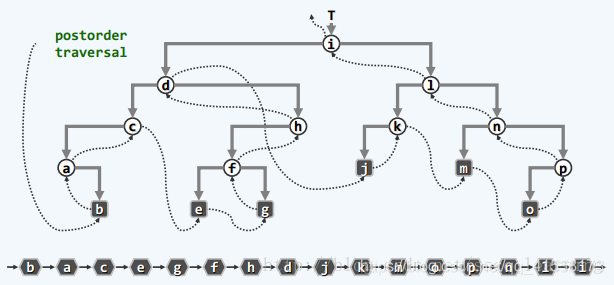
遍历:

void trav_mid_tree(tree* x)//后序遍历
{
    if (x == NULL) return;
    trav_mid_tree(x->left);
    trav_mid_tree(x->right);
        cout << x->val << ' ';
}

1、前序建树同时中序输出

3384.二叉树遍历
https://www.acwing.com/problem/content/description/3387/

void build()
{
    char c = getchar();
    if (c == '#') return;
    build();
    cout << c << ' ';
    build();
}

2、根据前序中序建树

3598.二叉树遍历
https://www.acwing.com/problem/content/3601/

根据先序遍历的性质，先序序列中的第一个元素就是根节点root。确定该点在中序序列中的位置k。

中序序列中：该位置的左边都是左子树，右边都是是右子树。

左子树的根节点就是根节点root的左孩子，右子树的根节点就是根节点root的右孩子。

递归到左子树和右子树。

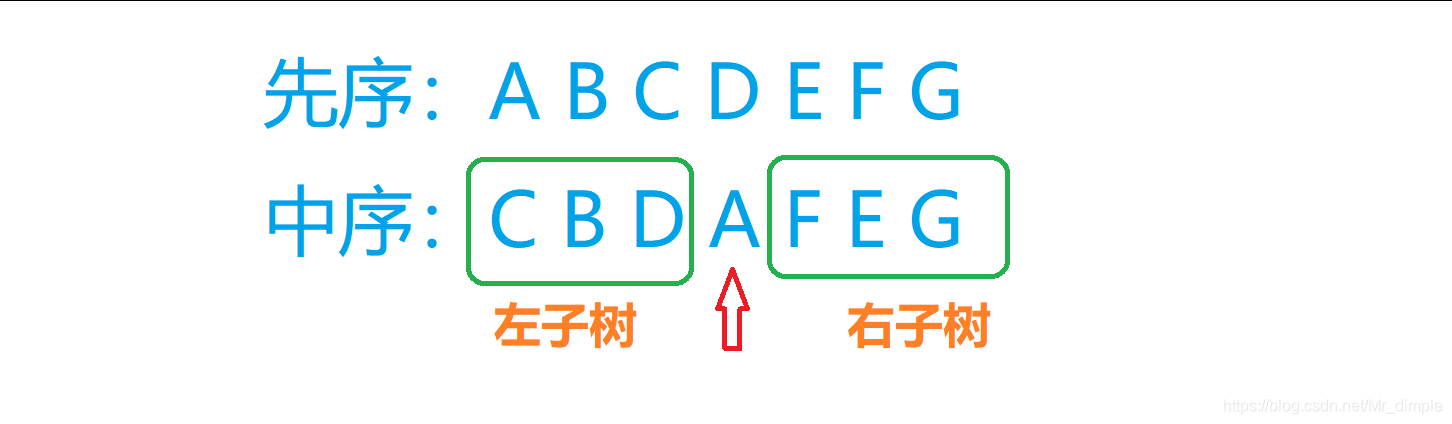
中序数列中左子树的个数：k-il

先序数列中左子树的个数：x-pl （x为左右子树分界线左边的一个位置，即图中D的位置）

两种数列左子树的个数是相等的，那么，x=k-il+pl

左子树的中序序列：il到k-1

左子树的先序序列：pl+1到k-il+pl

右子树的中序序列：k+1到ir

右子树的先序序列：k-il+pl+1到pr

Node* Build_Tree(int pl, int pr, int ml, int mr)
{
    int k = pos[s1[pl]];
    Node* root = new Node();
    root->data = s1[pl];
    if (k > ml)
        root->left = Build_Tree(pl+1, pl+k-ml, ml, k-1);
    if (k < mr)
        root->right = Build_Tree(pr+k-mr+1, pr, k+1, mr);

    cout << root->data;
    return root;
}

3、从上往下打印出二叉树的每个结点，同一层的结点按照从左到右的顺序打印。

BFS

43.不分行从上往下打印二叉树
https://www.acwing.com/problem/content/description/41/

vector<int> printFromTopToBottom(TreeNode* root) {
        vector<int> a;
        if (!root) return a;
        queue<TreeNode *> q;
        q.push(root);
        while (q.size())
        {
            TreeNode* t = q.front();
            q.pop();
            a.push_back(t->val);
            if (t->left != NULL)
                q.push(t->left);
            if (t->right != NULL)
                q.push(t->right);
        }
        return a;
    }