题目描述
7-1 求解迷宫从入口到出口的一条最短路径 (15 分)
求解迷宫从入口到出口的一条最短路径。输入一个迷宫,求从入口通向出口的一条可行最短路径。为简化问题,迷宫用二维数组 int maze[10][10]来存储障碍物的分布,假设迷宫的横向和纵向尺寸的大小是一样的,并由程序运行读入, 若读入迷宫大小的值是n(3<n<=10),则该迷宫横向或纵向尺寸都是n,规定迷宫最外面的一圈是障碍物,迷宫的入口是maze[1][1],出口是maze[n-2][n-2], 若maze[i][j] = 1代表该位置是障碍物,若maze[i][j] = 0代表该位置是可以行走的空位(0<=i<=n-1, 0<=j<=n-1)。求从入口maze[1][1]到出口maze[n-2][n-2]可以走通的路径。要求迷宫中只允许在水平或上下四个方向的空位上行走,走过的位置不能重复走,规定必须按向右、向下、向左、向上的顺序向前搜索试探,输出先到达出口的最短路径。 如下这样一个迷宫:
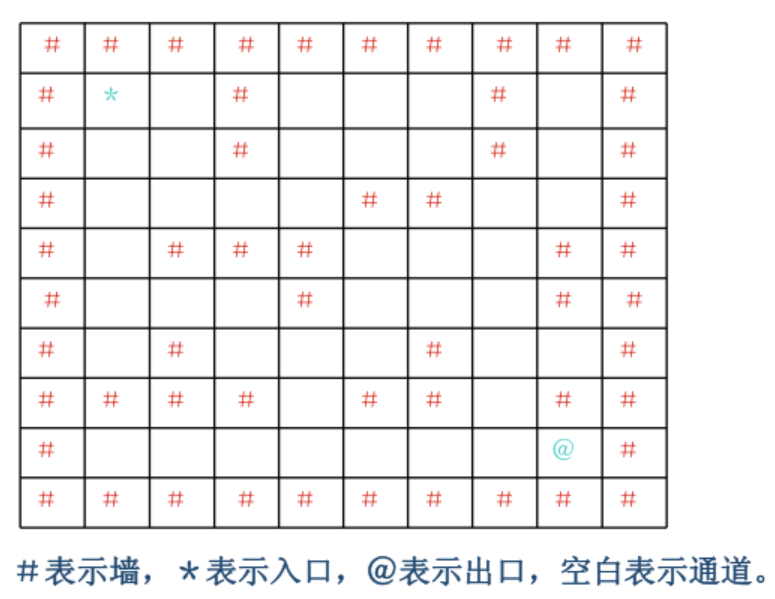
对应的二维数组表示: int maze[10][10]={ {1,1,1,1,1,1,1,1,1,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,0,0,1,1,0,0,1}, {1,0,1,1,1,0,0,0,1,1}, {1,0,0,0,1,0,0,0,1,1}, {1,0,1,0,0,0,1,0,0,1}, {1,1,1,1,0,1,1,0,1,1}, {1,0,0,0,0,0,0,0,0,1}, {1,1,1,1,1,1,1,1,1,1}};
输入格式:
输入迷宫大小的整数n, 以及n行和n列的二维数组(数组元素1代表障碍物,0代表空位)。
输出格式:
输出按规定搜索试探顺序先到达出口的首条最短路径,依次输出从入口到出口可行最短路径每个位置的行列下标(i,j),每个位置间用“,”分隔。若没有通路,输出:NO。
输入样例1:
4
1 1 1 1
1 0 1 1
1 0 0 1
1 1 1 1
输出样例1:
(1,1)(2,1)(2,2)
输入样例2:
10
1 1 1 1 1 1 1 1 1 1
1 0 0 1 0 0 0 1 0 1
1 0 0 1 0 0 0 1 0 1
1 0 0 0 0 1 1 0 0 1
1 0 1 1 1 0 0 0 0 1
1 0 0 0 1 0 0 0 0 1
1 0 1 0 0 0 1 0 0 1
1 0 1 1 1 0 1 1 0 1
1 1 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 1
输出样例2:
(1,1)(2,1)(3,1)(4,1)(5,1)(5,2)(5,3)(6,3)(6,4)(6,5)(7,5)(8,5)(8,6)(8,7)(8,8)
算法1
(bfs dfs)
bfs扩展出所有可能扩展出来的点,dfs求出所有可行路径
C++ 代码
#include<bits/stdc++.h>
using namespace std;
const int N=110;
typedef pair<int,int>PII;
struct A
{
int x,y;
}p[N][N];
int dx[]={0,1,0,-1},dy[]={1,0,-1,0};
int pa[N][N],vis[N][N];
int n,l,flag=0;
void bfs(int r,int t)
{
memset(vis,0,sizeof vis);
queue<A>q;
q.push({r,t});
vis[r][t]=1;
while(q.size())
{
A ans=q.front();
q.pop();
if(ans.x==n-2&&ans.y==n-2)
{
flag=1;
return;
}
for(int i=0;i<4;i++)
{
int xx=ans.x+dx[i],yy=ans.y+dy[i];
if(xx>0&&xx<n&&yy>0&&yy<n&&!vis[xx][yy]&&!pa[xx][yy])
{
vis[xx][yy]=1;
q.push({xx,yy});
p[xx][yy]=ans;
}
}
}
}
void print(A it)
{
if(it.x==1&&it.y==1)
{
printf("(%d,%d)",it.x,it.y);
return;
}
print(p[it.x][it.y]);
printf("(%d,%d)",it.x,it.y);
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
cin>>pa[i][j];
bfs(1,1);
if(!flag)
{
cout<<"NO"<<endl;
return 0;
}
A end={n-2,n-2};
print(end);
return 0;
}
存放路径问题模型
当前扩展出来的点存放上一个点的位置
p[下一个x坐标][下一个点y坐标]={上一个点x坐标,上一个点y坐标}
有点邻接矩阵的感觉了,不过存放的是上一个的信息
p[xx][yy]=ans;//下一个点的位置值存放上一个位置
void print(A it)
{
if(it.x==1&&it.y==1)
{
printf("(%d,%d)",it.x,it.y);//找到上一条路径坐标为(1,1)的点
return;//跳出后我们要回溯输出是上一个点的下一个点
}
print(p[it.x][it.y]);//回溯找到起点
printf("(%d,%d)",it.x,it.y);//输出上一个点对应的下一个点的坐标
}
练习: https://www.acwing.com/problem/content/description/1509/

