常用的排序算法:快速排序、归并排序,堆排序、计数排序(较常用)
排序方法分类
-
基于比较的方法
- 快速排序
- 归并排序
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序
- 堆排序
-
基于非比较(桶)的排序方法
- 计数排序
- 桶排序
- 基数排序
稳定性
- 稳定排序:冒泡、归并、插入 + 基于非比较的排序(计数、桶、基数)
- 不稳定排序:除了稳定的就是不稳定的,快排、选择、希尔、堆排
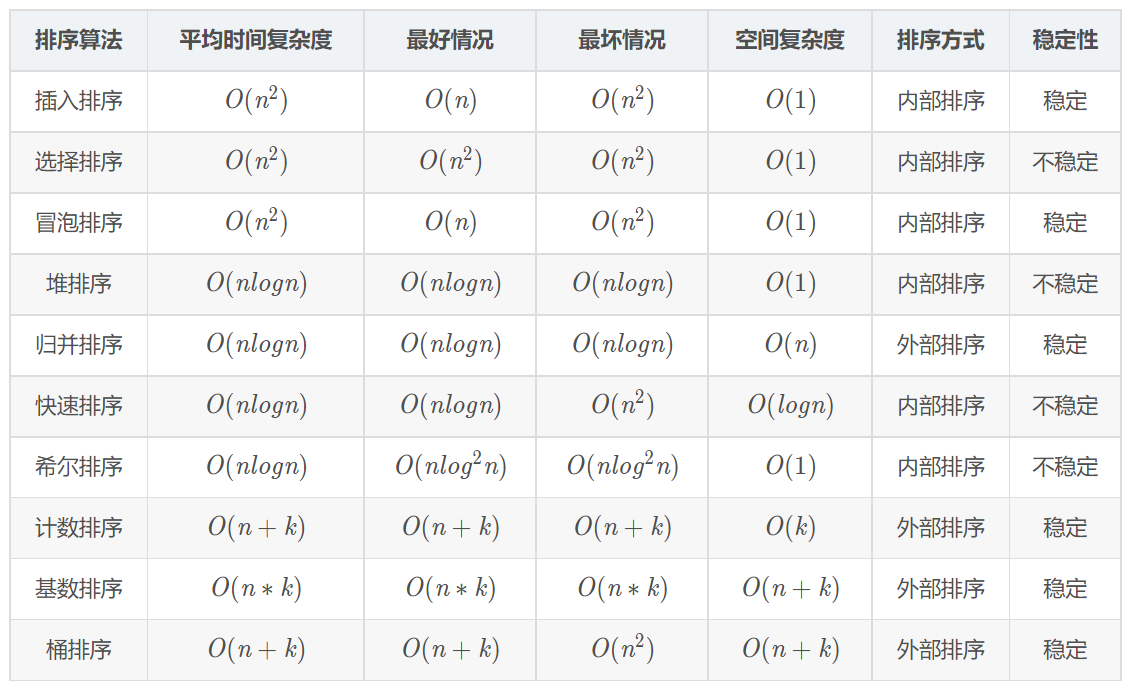
八大排序算法代码模板,桶排序实现方式比较多,基数排序基本不用,就不实现啦~
注意:这里堆排序下标从 1 开始处理比较方便。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
// 快速排序:找一个基准值 x,将比 x 大的数放到 x 的后面,比 x 小的数放到 x 的前面,递归左边部分和右边部分
void quickSort(vector<int>& nums, int l, int r) {
if (l >= r) return;
int mid = l + r >> 1;
int x = nums[mid], i = l - 1, j = r + 1;
while (i < j) {
do i ++ ; while (nums[i] < x);
do j -- ; while (nums[j] > x);
if (i < j) swap(nums[i], nums[j]);
}
quickSort(nums, l, j), quickSort(nums, j + 1, r);
}
// 归并排序:先向下拆分,直到每个区间只剩一个元素,然后两两区间进行两路归并排序,再往上合并,最后将排序后的数组放到原数组中。
void mergeSort(vector<int>& nums, int l, int r, vector<int>& tmp) {
if (l >= r) return;
int mid = l + r >> 1;
mergeSort(nums, l, mid, tmp), mergeSort(nums, mid + 1, r, tmp);
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r) {
if (nums[i] < nums[j]) tmp[k ++ ] = nums[i ++ ];
else tmp[k ++ ] = nums[j ++ ];
}
while (i <= mid) tmp[k ++ ] = nums[i ++ ];
while (j <= r) tmp[k ++ ] = nums[j ++ ];
for (int i = l, k = 0; i <= r; i ++ ) nums[i] = tmp[k ++ ];
}
// 冒泡排序:比较相邻两个元素的大小,将最大的元素放到数组的末尾,每次排序可以确定一个值的位置,最多经过 n - 1 趟排序即可排序完成
void bubbleSort(vector<int>& nums) {
for (int i = 0; i < nums.size(); i ++ ) {
for (int j = 0; j < nums.size() - i - 1; j ++ ) {
if (nums[j] > nums[j + 1])
swap(nums[j], nums[j + 1]);
}
}
}
// 选择排序:每次选择一个较小值从前往后依次放,直到所有数都放到了该放的位置
void selectSort(vector<int>& nums) {
for (int i = 0; i < nums.size(); i ++ ) {
int minIndex = i;
for (int j = i + 1; j < nums.size(); j ++ ) {
if (nums[j] < nums[minIndex])
minIndex = j;
}
if (minIndex != i)
swap(nums[minIndex], nums[i]);
}
}
// 插入排序:维护两个区间,一个是已排序区间, 初始状态只有第一个数,另一个是未排序区间,每次从未排序区间中取一个数 x,从已排序区间中找到小于 x 的位置 j,然后将其放到 j + 1 位置上,直到所有数都插入完成。
void insertSort(vector<int>& nums) {
for (int i = 1; i < nums.size(); i ++ ) {
int x = nums[i], j = i - 1;
while (j >= 0 && nums[j] >= x) {
nums[j + 1] = nums[j];
j -- ;
}
nums[j + 1] = x;
}
}
// 插入排序 2:和方法 1 思想是一样的,区别就是:不采用向后移动元素的方式插入,而是用交换的方式找到这个数应该放的位置。
void insertSort2(vector<int>& nums) {
for (int i = 1; i < nums.size(); i ++ ) {
for (int j = i - 1; j >= 0 && nums[j] >= nums[j + 1]; j -- )
swap(nums[j], nums[j + 1]);
}
}
// 希尔排序:对比 [插入排序 2] 记忆;首先将数组进行分组,组内再用插入排序进行排序,最后合并起来就是排序后的结果。
void shellSort(vector<int>& nums) {
int n = nums.size();
for (int gap = n / 2; gap > 0; gap /= 2) {
for (int i = gap; i < n; i ++ ) {
for (int j = i - gap; j >= 0 && nums[j] >= nums[j + gap]; j -= gap) {
swap(nums[j], nums[j + gap]);
}
}
}
}
// 堆 - 向下调整:找出当前节点 u 和左右儿子值的的最大者 t,如果当前节点 u 不是最大值,那么将 u 和 t 的值交换,此时节点 u 是堆顶且是最大值,递归向下调整节点 t
void down(vector<int>& nums, int n, int u) {
int t = u, left = u * 2, right = u * 2 + 1;
if (left <= n && nums[left] > nums[t]) t = left;
if (right <= n && nums[right] > nums[t]) t = right;
if (u != t) {
swap(nums[u], nums[t]);
down(nums, n, t);
}
}
// 堆排序 - 下标从 1 开始
void heapSort(vector<int>& nums, int size) {
int n = size;
// 建堆
for (int i = n / 2; i >= 1; i -- ) down(nums, n, i);
// 堆排序:每次将堆顶和待排序区间的最后一个元素交换,然后新的堆顶再向下调整
for (int i = 1; i <= size; i ++ ) {
swap(nums[1], nums[n]);
n -- ;
down(nums, n, 1);
}
}
// 堆排序 - 下标从 0 开始
/*void down(vector<int>& nums, int n, int u) {
int t = u, left = u * 2, right = u * 2 + 1;
if (left <= n && nums[left] > nums[t]) t = left;
if (right <= n && nums[right] > nums[t]) t = right;
if (u != t) {
swap(nums[u], nums[t]);
down(nums, n, t);
}
}
void heapSort(vector<int>& nums, int size) {
int n = size;
// 建堆
for (int i = n / 2; i >= 1; i -- ) down(nums, n, i);
// 堆排序
for (int i = 1; i <= size; i ++ ) {
swap(nums[1], nums[n]);
n -- ;
down(nums, n, 1);
}
}*/
// 计数排序:开数组数值范围的桶,每个元素一个桶,每个桶记录每个元素出现的次数,最后遍历桶输出
void countingSort(vector<int>& nums) {
int n = nums.size();
// 开一个桶,假设最大值是 100
vector<int> cnt(101, 0);
// cnt 记录每个元素出现的次数
for (int i = 0; i < n; i ++ ) cnt[nums[i]] ++ ;
for (int i = 0, k = 0; i <= 100; i ++ ) {
// 将桶里的数放到原数组中
while (cnt[i]) {
nums[k ++ ] = i;
cnt[i] -- ;
}
}
}
int main()
{
/* 测试数据
2
5
5 2 3 1 4
10
6 8 1 3 2 5 9 7 4 0
*/
int T;
cin >> T;
while (T -- ) {
int n;
cin >> n;
vector<int> nums(n);
for (int i = 0; i < n; i ++ ) cin >> nums[i];
// quickSort(nums, 0, nums.size() - 1);
// vector<int> tmp(n);
// mergeSort(nums, 0, nums.size() - 1, tmp);
// bubbleSort(nums);
// selectSort(nums);
// insertSort(nums);
// insertSort2(nums);
// shellSort(nums);
// vector<int> nums(n + 1);
// for (int i = 1; i <= n; i ++ ) cin >> nums[i];
// heapSort(nums, n); // 堆排序下标从 1 开始比较好写,其他排序从 0 开始
// for (int i = 1; i <= n; i ++ ) cout << nums[i] << " ";
// countingSort(nums);
for (int i = 0; i < n; i ++ ) cout << nums[i] << " ";
cout << endl;
}
return 0;
}
参考资料:

