【学习笔记】树形DP
一,定义
当前状态从子节点到父节点(自下而上),或者从父节点转移到字节点(自上而下),用来解决可抽象成树形结构且具有最优子结构的问题,第一维通常是节点编号
二,类似于状态机的树上DP
1.【状态机】
如下图所示
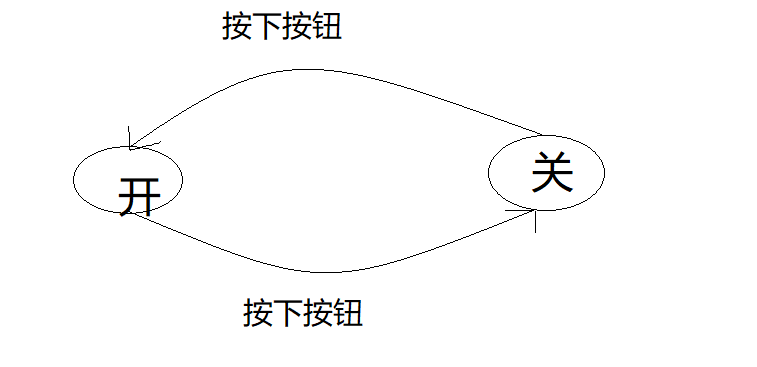
假设入口状态为关,经过按下按钮这个行为可以转移到开,相反也是如此,即能够根据问题的中隐含的规则按照预先设定的状态进行状态转移
2.【例题】
(1)没有上司的舞会
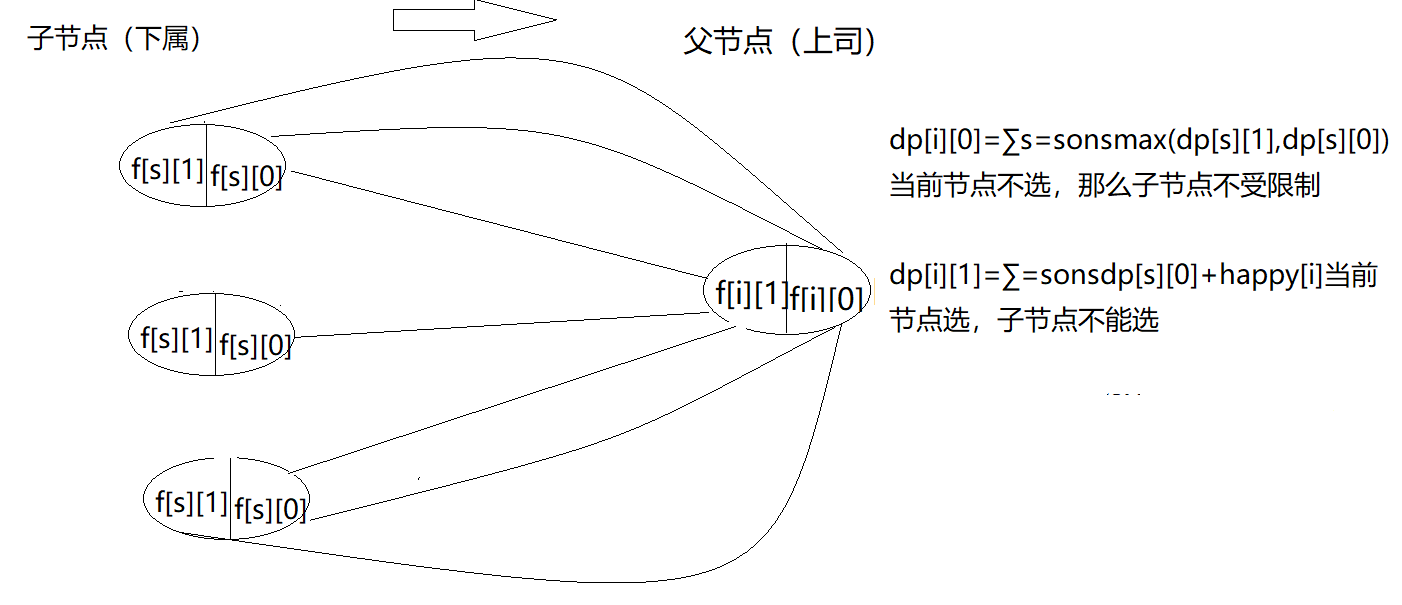
- 解析: 由题目描述可知,上司和员工的关系可以转换成具有N个节点,N-1条边的树形结构(父节点为上司,其子节点为他的直接下属),先只考虑当前节点的状态转移,当前节点的曲法取决与其子节点(下属)。
- 状态表示:每个人只有两种状态,则设f[i][0]为第i个人不来,他的下属所能获得的最大快乐值;f[i][1]为第i个人来,他的下属所能获得的最大快乐值。
- 状态转移:f[i][0]=∑s=sonsmax(dp[s][1],dp[s][0]) — 如果自己不来,那么他的下属可以来或者不来,取最大值。
dp[i][1]=∑s=sonsdp[s][0]+happy[i] — 如果自己来了,那么他的下属就不来了,只能从下属(子节点)选择不来的状态转移过来
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 6010;
int n;
int h[N], e[N], ne[N], iex;
int happy[N];
int f[N][2];
bool has_fa[N];
void add(int a,int b){
e[iex] = b ,ne[iex] = h[a],h[a] = iex++;
}
void dfs(int u){
f[u][1] = happy[u];
for(int i = h[u] ; ~i ; i = ne[i]) // 枚举每个子节点
{
int j = e[i];
dfs(j); // 先算出来子节点,再算自己(自下而上)
f[u][1] += f[j][0];
f[u][0] += max(f[j][0],f[j][1]);
}
}
int main(){
scanf("%d",&n);
for(int i = 1 ; i <= n ; i++)
scanf("%d",&happy[i]);
memset(h,-1,sizeof(h));
for(int i = 0 ; i < n-1 ; i++)
{
int a,b;
scanf("%d%d",&a,&b);
add(b,a);
has_fa[a] = true;
}
int root = 1;
while(has_fa[root]) root++; // 找出根节点
dfs(root);
printf("%d\n",max(f[root][1],f[root][0])); //
return 0;
}
背包问题树形·DP(有树形依赖的背包问题)
1.【定义】
实际上是背包与树形DP的结合。状态转移时间,把子节点当做一个背包,,除了以节点编号作为DP的阶段,通常也需要报当前的背包的“体积”作为第二维状态。实际上,我们要处理的问题就是一个分组背包问题。
2,【状态转移】
把每个节点看作一类物品,状态转移相当于一个分组背包问题。
3,【例题】
3.1.1 选课
- 解析:把每个子节点看做一个未装满的背包。
- 状态转移:以当前节点当做容量为M的背包,把各个子节点分别当一类物品(包含多个物品),状态转移和分组背包一样,只不过略去了第几个物品那一位,所以物品容量要从大到小枚举。

3.1.2【代码】
#include <iostream>
#include <cstring>
using namespace std;
const int N = 310;
int n ,m, idx;
int h[N],w[N],e[N],ne[N];
int f[N][N];
void add(int a,int b,int c){
e[idx] = b , ne[idx] = h[a] , w[idx] = c , h[ a ] = idx++;
}
void dfs(int u,int fa)
{
for(int i = h[u] ; ~i ;i = ne[i])
{
int j = e[i];
if(j == fa)continue; // 判重
dfs(j,u);
for(int k = m ;k >= 0 ; k--)
for(int h = 0 ; h <= k - 1 ;h++)
f[u][k] = max(f[u][k] , f[u][k - h - 1] + f[j][h] + w[i]) ; //枚举每个背包
}
}
int main(){
memset(h,-1,sizeof(h));
cin >> n >> m;
int a,b;
for(int i = 1 ; i <= n ;i++)
{
cin >> a >> b;
add(a,i,b);
}
dfs(0,-1);
cout << f[0][m] << endl;
return 0;
}
3.2【例题二】
3.2.1 二叉苹果树
与上题类似,不作过多赘述
3.2.2【代码】
#include <iostream>
#include <cstring>
using namespace std;
const int N = 110 , M = N * 2;
int e[M],w[M],ne[M],h[N],f[N][N];
int n,m,idx;
void add(int a,int b,int c){
e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx++;
}
int dfs(int u ,int fa){
for (int i = h[u]; ~i; i = ne[i])
{
if (e[i] == fa) continue;
dfs(e[i], u);
for (int j = m; j; j -- )
for (int k = 0; k + 1 <= j; k ++ )
f[u][j] = max(f[u][j], f[u][j - k - 1] + f[e[i]][k] + w[i]);
}
}
int main(){
cin >> n >> m;
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
dfs(1, -1);
cout << f[1][m] << endl;
return 0;
}
二次扫描换根
2,【定义】
一般用于解决不定根问题,第一次扫描,任选一个根,在“有根树”上执行树形DP,也就是回溯时发生的,自底向上的状态转移;第二次扫描从刚才的根乘法,对一般用于解决不定根问题,第一次扫描,任选一个根,在“有根树”上执行树形DP,也就是回溯时发生的,自底向上的状态转移;第二次扫描从刚才的根乘法,对整棵树执行一次DFS,在每次换根进行自顶向下的推导,计算出“换根” 后的解。 ----引用自《算法竞赛进阶指南》
3,【例题】
积蓄程度
- 解析:第一次扫描 把当前节点当做源点,向下DFS求出能流出多少水,第二次自上而下DFS求出每个节点向父节点能流多少水
- 状态转移:见代码
- 注意:两次扫描都需y要考虑是否为叶子节点,如果为叶子节点,流向该叶子节点的水即为连改节点的边的边权
3.1【代码】
#include <iostream>
#include <cstring>
using namespace std;
const int N = 2e5 + 10 , M = 2 * N;
int n ,idx;
int h[N],w[M],e[M],ne[M];
int d[N],f[N],ed[N];
void add(int a,int b,int c)
{
e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx++;
}
int dfs_d(int u,int fa){
for(int i = h[u] ; ~i ; i = ne[i])
{
int j = e[i];
if(j == fa)continue;
if(ed[j] == 1)d[u] += w[i];
else d[u] += min(dfs_d(j,u) , w[i]);
}
return d[u];
}
void dfs_u(int u,int fa){
for(int i = h[u] ; ~i ; i = ne[i])
{
int j = e[i];
if(j == fa)continue;
if(ed[u] == 1)f[j] = d[j] + w[i];
else f[j] = d[j] + min(f[u] - min(d[j] , w[i]) , w[i]);
dfs_u(j,u);
}
}
int main(){
int cnt;
cin >> cnt;
while(cnt--)
{
memset(h,-1,sizeof(h));
memset(d,0,sizeof(d));
memset(f,0,sizeof(f));
memset(ed,0,sizeof(ed));
idx = 0;
cin >> n;
int a,b,c;
for(int i = 0 ; i < n - 1 ;i++)
{
cin >> a >> b >> c;
add(a,b,c),add(b,a,c);
ed[a] ++ , ed[b] ++ ;
}
dfs_d(1,-1);
f[1] = d[1];
dfs_u(1,-1);
int res = 0;
for(int i = 1 ; i <= n ;i++)res = max(res,f[i]);
cout << res << endl;
}
return 0;
}
3.2【例题二】
大臣的旅费
- 解析:二次扫描加换根求出树的最长路径
- 状态转移:见代码
- 注意:由题意可知,起步价为10元,大臣每多走一km就要多1元钱,所以答案是一个以最长路径为末项的等差数列和
3.2.1【代码】
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10 , M = 2 * N;
int n,idx;
int h[N],e[M],ne[M],w[M];
int d1[N],d2[N],up[N];
int p[N];
void add(int a,int b,int c){
e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx++;
}
int dfs_d(int u,int fa){
for(int i = h[u] ;~i ;i= ne[i])
{
int j = e[i];
if(j == fa)continue;
int d = dfs_d(j,u) + w[i];
if(d > d1[u])
{
d2[u] = d1[u],d1[u] = d;
p[u] = j;
}
else if(d > d2[u])d2[u] = d;
}
return d1[u];
}
void dfs_u(int u,int fa)
{
for(int i = h[u] ;~i ;i= ne[i])
{
int j = e[i];
if(j == fa)continue;
if(p[u] == j)up[j] = max(up[u] , d2[u]) + w[i];
else up[j] = max(up[u] , d1[u]) + w[i];
dfs_u(j,u);
}
}
int main(){
cin >> n;
int a,b,c;
memset(h,-1,sizeof(h));
for(int i = 0 ; i < n - 1 ; i++)
{
cin >> a >> b >> c;
add(a,b,c),add(b,a,c);
}
dfs_d(1,-1);
dfs_u(1,-1);
int ans = 0;
for(int i = 1 ; i <= n ;i++)
ans = max(ans,max(d1[i] + d2[i] , d1[i] + up[i]));
cout << ans * 10 + ans * (ans + 1ll ) / 2 << endl;
return 0;
}
*
3.3【例题三】
旅游规划
- 解析:用二次扫描求出最长路径即可,并输出最长路径的所有节点,用一个循环判断即可,具体见代码
3.3.2【代码】
#include <iostream>
#include <cstring>
using namespace std;
const int N = 2e5 + 10 , M = 2 * N ;
int d1[N],d2[N],p[N],up[N];
int h[N],e[M],ne[M];
int idx,n;
int maxd;
void add(int a,int b)
{
e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}
int dfs_d(int u,int fa){
d1[u] = 0,d2[u] = 0;
int dist = 0;
for(int i = h[u] ; ~i ; i = ne[i])
{
int j = e[i];
if(j == fa)continue;
int d = dfs_d(j,u) + 1;
dist = max(d,dist);
if(d > d1[u]){
d2[u] = d1[u] , d1[u] = d;
p[u] = j;
}
else if(d > d2[u])d2[u] = d;
}
maxd = max(maxd, d1[u] + d2[u]);
return dist;
}
void dfs_u(int u,int fa){
for(int i = h[u] ; ~i ;i = ne[i])
{
int j = e[i];
if(j == fa)continue;
if(p[u] == j)up[j] = max(up[u],d2[u]) + 1;
else up[j] = max(up[u],d1[u]) + 1;
dfs_u(j,u);
}
}
int main(){
cin >> n;
int a,b;
memset(h,-1,sizeof(h));
for(int i = 0 ; i < n ;i++)
{
cin >> a >> b;
add(a,b),add(b,a);
}
dfs_d(0,-1);
dfs_u(0,-1);
int res = up[0];
for(int i = 0 ; i < n ;i++)res = max(up[i] + d1[i], res);
//if(d1[0] + d2[0] == res) cout << 0 << endl;
for(int i = 0 ; i < n;i++)
if(up[i] + d1[i] == res || d1[i] + d2[i] == res)
cout << i << endl;
return 0;
}
3.4,【例题四】
数字转换
- 解析:利用小于当前数约数之和作为父节点,当前数为子节点建树,求出该树的最长路径即可
3.4.1【代码】
#include <iostream>
#include <cstring>
using namespace std;
const int N = 5e4 + 10;
int h[N],ne[N],e[N];
int sum[N];
int idx,n,ans;
void add(int a,int b)
{
e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}
int dfs(int u,int fa){
int dist = 0;
int d1 = 0 , d2 = 0;
for(int i = h[u] ;~i ;i = ne[i])
{
int j = e[i];
int d = dfs(j,u);
dist = max(dist,d);
if(d > d1)d2 = d1 , d1 = d; // 求出改节点最长路径和次短路径
else if(d > d2)d2 = d;
}
ans = max(ans,d1 + d2);
return dist + 1;
}
int main(){
cin >> n;
memset(h,-1,sizeof(h));
for(int i = 1 ; i <= n ; i++)
for(int j = 2 ; j <= n / i ;j++)
sum[j * i] += i; // 算出每个数的约数和
for(int i = 2 ; i <= n ;i++)
if(i > sum[i])
add(sum[i],i); //如果该数的约数和小于该数,那么就从约数和向该数连一条单向边
dfs(1,-1);
cout << ans << endl;
return 0;
}


Sto Orz
tgl%%%