$A: Acwing4311.$最小值

将分数比较大小转化成乘积来比较

#include<bits/stdc++.h>
using namespace std;
const int N = 5010;
int main()
{
    int n, m, a, b, c, d;
    cin >> n >> m >> a >> b;
    n --;
    while (n --)
    {
        cin >> c >> d;
        if (a * d > b * c) a = c, b = d;
    }
    printf("%.6f", ((double)(m * a) / b));
    return 0;
}

$B: Acwing4312.$ 出现次数

阴间$KMP$

用$T$在每个$(l,r)$区间内做$kmp$
时间复杂度$O(n^2)$
计算上界$1e8$，过不过看评测鸡心情。

#include<bits/stdc++.h>
using namespace std;
const int M = 1010, N = 1010;
char p[M], s[N];
int ne[M];

int main(){
    cin.tie(0); cout.tie(0);
    ios::sync_with_stdio(false);
    int n, m, k;
    cin >> n >> m >> k >> s + 1 >> p + 1;
    // s是模式串，p是匹配串
    while (k --)
    {
        int l, r; cin >> l >> r;
        if (r - l + 1 < m) 
        {
            cout << '0' << endl;
            continue;
        }
        for(int i = 2, j = 0; i <= m; i ++)
        {
            while(j && p[i] != p[j+1]) j = ne[j];
            if(p[i] == p[j + 1]) j++;
            ne[i] = j;
        }
        int cnt = 0;
        for(int i = l, j = 0; i <= r; i ++){
            while(j && s[i] != p[j + 1]) j = ne[j];
            if(s[i] == p[j + 1]) j++;
            if(j == m){
                cnt ++;
                j = ne[j];
            }
        }
        cout << cnt << endl;
    }
    return 0;
}

正解

因为$T$字符串是固定的，所以可以直接预处理出来T数组在$S$数组中出现次数的前缀和。然后查询就可以$O(1)$。
$Ps:$ 注意$s[i]$为以$i$结尾的所有满足条件的$T$，如果要求$(l,r)$区间内的，$l$应该起码满足可以放下一个$T$

$C: Acwing.4313$满二叉树等长直径

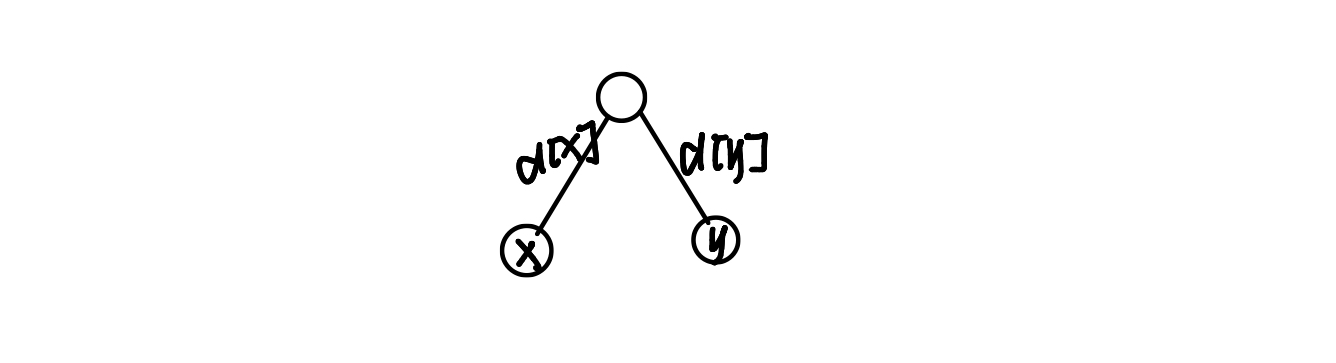
考虑只有两个子节点的情况，要将$d[x]$,$d[y]$变成一致，易知只需将两者中小的那个增大到大的那个即可。即花费$abs(d[x] - d[y])$

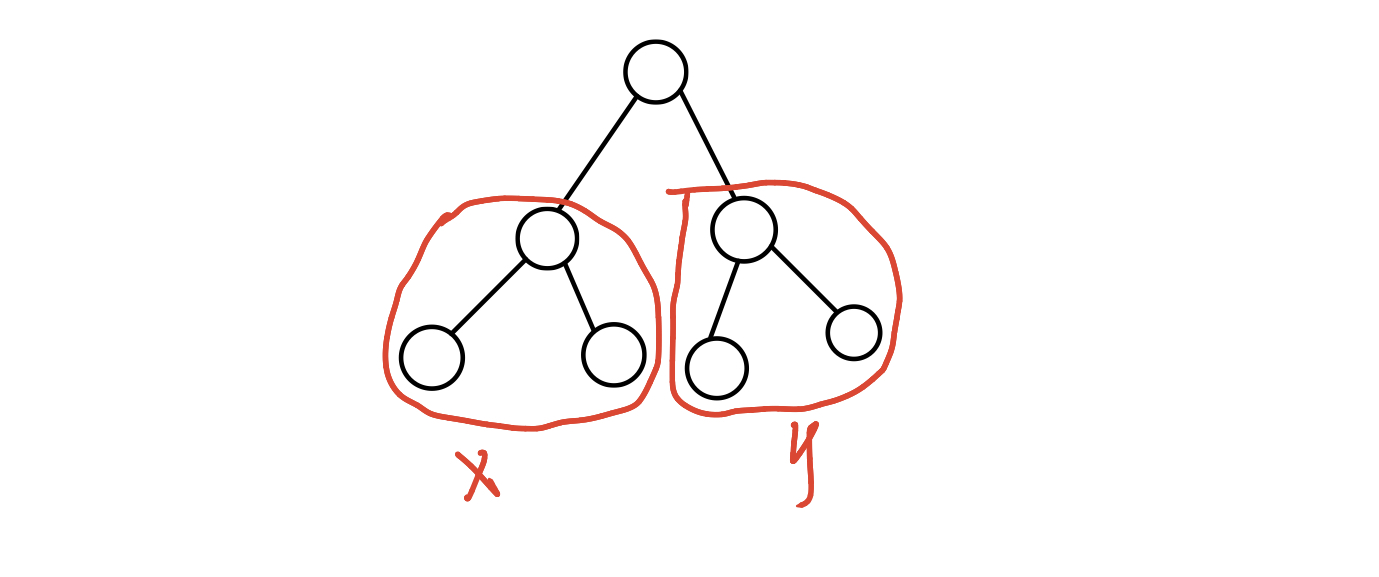
所以可以将两个子树都看成一个整体，每个子树整体内的点到根节点的距离都已经达到相同，所以可以采用上面类似的贪心思想。

#include<bits/stdc++.h>
using namespace std;
const int N = 2500;
int a[N], d[N], res;
int main()
{
    int n; cin >> n;
    for (int i = 2; i <= pow(2, n + 1); i ++)
    {
        scanf("%d", &a[i]);
        d[i] = a[i] + d[i / 2];
    }
    for (int i = pow(2, n + 1) - 1; i > 1;)
    {
        d[(i - 1) / 2] = max(d[i], d[i - 1]);
        res += (max(d[i], d[i - 1]) - min(d[i], d[i  -1]));
        i -= 2;
    }
    cout << res;
    return 0;
}