c第五讲 动态规划

一、背包问题

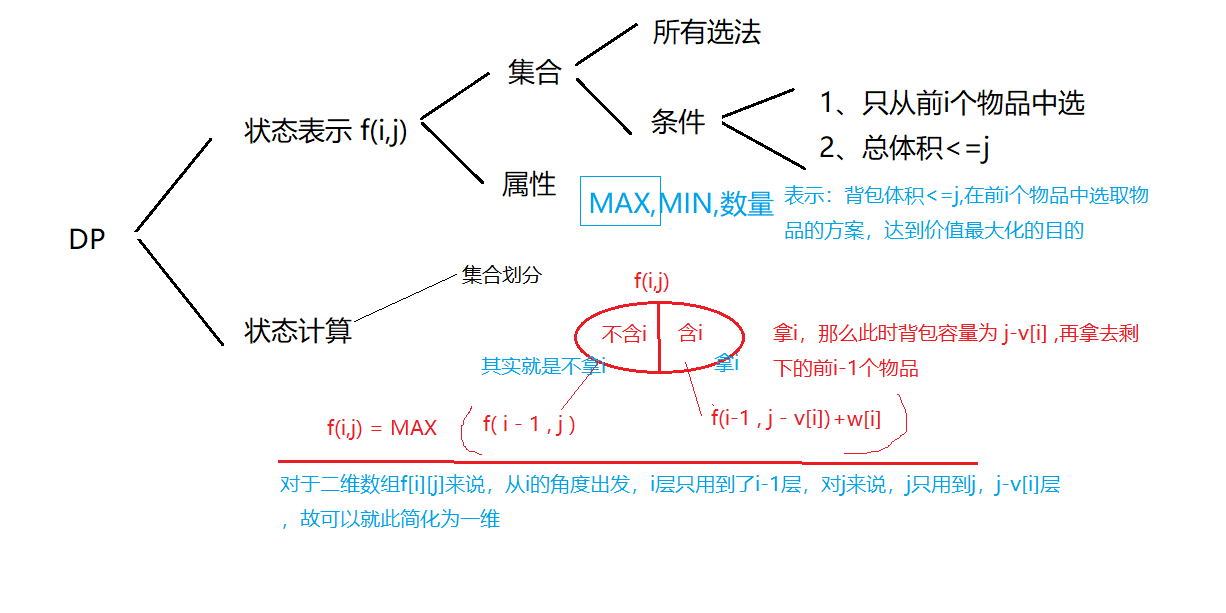
1.1、01背包问题

二维转化到一维的问题：

二维

const int N = 1100;
 int n,m;
 int v[N],w[N];
 int f[N][N];

 int main(){
    cin >> n >> m;

    for(int i = 1;i <= n;i++){
        cin >> v[i] >> w[i];
    }
    cout << "j   :  ";
    for(int j = 0;j <= m;j++){
        cout << j << ' ';
    }cout << endl;
    for(int i = 1;i <= n;i++){ // 前i个物品
    cout<< "v["<< i <<"]:" << v[i] << ' ';
        for(int j = 0;j <= m;j++){//背包容量
            //不拿
            f[i][j] = f[i-1][j];
            //拿
            if(j >= v[i])f[i][j] = max(f[i][j] , f[i-1][j - v[i]] + w[i]); 
            cout << f[i][j] << ' ';
        }
        cout << endl;
    }

    cout << f[n][m] << endl;

    return 0;
 }

一维：

const int N = 1100;
 int n,m;
 int v[N],w[N];
 int f[N];
 int main(){
    cin >> n >> m;

    for(int i = 1;i <= n;i++){
        cin >> v[i] >> w[i];
    }
    /*
    一维化：
    对于 i ，只需要使用到i  i-1 层，故去掉f[i]

    对于j，有f[j],f[j - v[i]] + w[i]的情况


    */
    cout << "j   :  ";
    for(int j = 0;j <= m;j++){
        cout << j << ' ';
    }cout << endl;

    for(int i = 1;i <= n;i++){ // 前i个物品
        cout << "v["<<i << "]"<<v[i] << ':';
        //for(int j = v[i];j <= m;j++){//背包容量
        for(int j = m;j >= v[i] ;j--){

            f[j] = max(f[j],f[j - v[i]] + w[i]);

            cout << f[j] << ' ';
            //f[i][j] = max(f[i][j] , f[i-1][j - v[i]] + w[i]); 
        }
        cout << endl;
    }

    cout << f[m] << endl;

    return 0;
 }

1.2、完全背包

完全背包的意思是，每个物品都有无数份，就需要我们去 取极限。

对于存在物品/数字可以无限次选取的情况，可以考虑完全背包

const int N = 1100;
 int n,m;
 int v[N],w[N];
 int f[N];
 int main(){
    cin >> n >> m;
    for(int i = 1;i <= n;i++){
        cin >> v[i] >> w[i];
    }
    for(int i = 1;i <= n;i++){
        //for(int j = 0; j <= m ;j ++){
        for(int j = v[i]; j <= m ;j ++){
            //for(int k = 0 ; k * v[i]<= j; k ++){

            //f[i][j] = max(f[i][j] , f[i-1][j - v[i] * k] + w[i] * k);
            //二维
            //f[i][j] = f[i-1][j];
            //if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
            //一维
            f[j] = max(f[j], f[j - v[i]] + w[i]);
            //}
        }
    }
    /**
    01背包是当前物品 i 在前面i-1个物品的基础上对i机械能选择
    完全背包是在当前物品i中，对物品进行分成k段，在第k-1段基础上对第k段进行选择
    其实还是在第i个物品中选择。
    */
    return 0;
 }

1.3、多重背包

多重背包的意思是，每个物品都是有限份s[i]，那么就与01背包类似，对于当前物品i，有不拿 f[i,j] = f[i-1,j] 和拿多少份的问题f[i-1,j - v[i] * k] + w[i] * k

对于物品/数字是有限个的情况可以考虑多重背包

int main(){
    cin >> n >> m;s
    for(int i = 1;i <= n;i++){
        cin >> v[i] >> w[i] >> s[i];
    }
    //f[i][j] = max(f[i-1][j - v[i] * k] + w[i]); k = 0,1,2,...s[i]
    for(int i = 1;i <= n;i++){
        for(int j = 0;j <= m;j++){
            for(int k = 0;k <= s[i] && k * v[i] <= j; k++){
                f[i][j] = max(f[i][j],f[i-1][j - v[i] * k] + w[i] * k);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
 }

多重背包一维优化

const int N = 2e7;
 int n,m;
 int v[N],w[N];
 int f[N];
 int main(){
    cin >> n >> m;
    int cnt = 0;    
    for(int i = 1;i <= n;i++){
        int a,b,s;
        cin >> a >> b >> s;
        int k = 1;

        int curs = s;
        int start = cnt+1;      
//  将s进行二进制拆分
//  a体积  b 价值  s总数
//  把s拆分成1 2 4 8 .. 份 并计算每一份的体积、价值 存入数组中 ，最后在01背包遍历一遍
        while(k <= s){
            cnt++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }   
        if(s > 0){
            cnt++;
            v[cnt] = a * s;
            w[cnt] = b * s;
         }

        cout << a << " " << b <<' ' << curs << " : "<< endl;
        for( ;start<=cnt;start++){
            cout << v[start] << "-->" << w[start] << endl;
        }
    }
    cout << "======================" << endl;
    for(int i = 1 ;i<=cnt;i++){
        cout << v[i] << "-->" << w[i] << endl;
    }
    n = cnt;
    for(int i = 1;i <= n;i++){
        for(int j = m;j >= v[i];j--){
            f[j] = max(f[j],f[j - v[i]] + w[i]);
        }
    }
    cout << f[m] << endl;
    return 0;
 }

1.4、分组背包

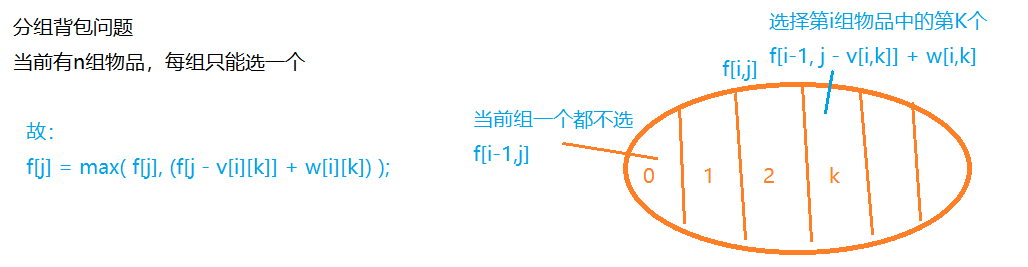
const int N = 110;
int n,m;
int v[N][N],w[N][N];
int f[N][N],s[N];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i++){
        cin >> s[i];
        for(int j = 0;j < s[i];j++){
            cin >> v[i][j] >> w[i][j];
        }   
    }
    for(int i = 1;  i <= n;i++){
        for(int j = 0;j <= m;j++){
            f[i][j] = f[i-1][j]; //  这里需要注意 不拿是在第二个for里面  因为第三个for循环代表的意思是拿第i组中的第k个
            for(int k = 0;k < s[i];k++){    
                if(v[i][k] <= j){
                    f[i][j] = max(f[i][j], f[i-1][j - v[i][k]] + w[i][k]);
                }
            }
        }   
    }
    cout << f[n][m] << endl; 
    return 0;
}

分组背包一维优化

 const int N = 110;
 int n,m;
 int v[N][N],w[N][N],s[N];
 int f[N];
 int main(){
    cin >> n >> m;
    for(int i = 1;i <= n;i++){//n组
        //改组物品数量
        cin >> s[i];
        for(int j = 0;j < s[i];j++){
            cin >> v[i][j] >> w[i][j];
         }
    }
//在每一组中选择第0、1、2...件物品，
// 不拿 f[i][j] = f[i-1][j]   拿第k件物品：f[i-1][j - v[i][k] ]
//一维化就是f[j] = max(f[i]  ,  f[i-1][j - v[i][j - v[i][k]]])
    for(int i = 1;i <= n;i++){
        for(int j = m;j >= 0;j--){
            for(int k = 0;k < s[i];k++){
                if(v[i][k] <= j)
                    f[j] = max( f[j], (f[j - v[i][k]] + w[i][k]) );

            }
        }
    }
    cout << f[m] << endl;
    return 0;
 }

二、线性DP

2.1、数字三角形

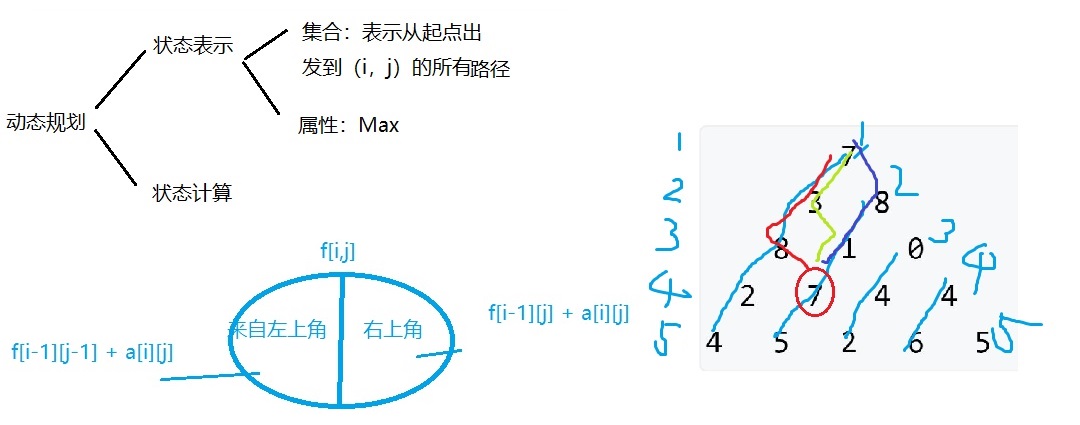
const int N = 520,INF = 1e9;
int n,a[N][N],f[N][N];

int main(){

    cin >> n;

    for(int i = 1;i <= n;i++){
        for(int j = 1;j <= i;j++){
            cin >> a[i][j];
        }
    }   

    for(int i = 0;i <= n;i++){
        for(int j = 0;j<=i;j++){
            f[i][j] = -INF;
        }
    }
    f[1][1] = a[1][1];
    for(int i = 2;i <= n;i++){
        for(int j = 1; j <= i;j++){
            f[i][j] = max(f[i-1][j-1] + a[i][j],  f[i-1][j]+ a[i][j]);
        }
    }
    int res = -INF;
    //对最底层进行一次遍历
    for(int i = 1;i<=n;i++){
        res = max(res,f[n][i]);
    }
    cout << res << endl;
    return 0;
}

2.2、 最长上升子序列

const int N = 1010;
int n,a[N],f[N],g[N];

int main(){

    cin >> n;

    for(int i = 1; i<= n;i++){
        cin >> a[i];
    }
//还可以保存最长上升子序列 g
    for(int i = 1; i <= n; i++){
        f[i] = 1;
        g[i] = 0;
        for(int j = 1; j < i;j++){
            if(a[j] < a[i]){
                if(f[i] < f[j] + 1){
                    f[i] = f[j] + 1;
                    g[i] = j;   
                }
                //f[i] = max(f[i], f[j] + 1);
            }
        }
    }
    int k = 1;
    int res = 0;
    for(int i = 1;i <= n;i++){
        if(f[k] < f[i]){
            k = i;
        }
        res = max(res,f[i]);
    }
//  for(int i = 0;i <= res;i++){
//      cout << a[k] << ' ';
//      k = g[k];
//  }   


    cout << res << endl;
    return 0;
}

2.2.1、优化1

最长上升子序列的时间复杂度为O(n^2)，对于数据超过1e5就会超时。

//  不用库函数，用 二分模板来找
const int N = 100010;
int n;
int a[N];
int st[N];
int tt = 0;
int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);

    st[tt] = a[0];
    for(int i = 1 ; i < n ; i++)
    {
        if(a[i] > st[tt]) st[++ tt] = a[i];
        else 
        {
            int l = 0 , r = tt;
            while(l < r)
            {
                int mid = (l + r) >> 1;
                if(st[mid] >= a[i]) r = mid;
                else l = mid + 1;
            }
            st[l] = a[i];
        }
    }

    printf("%d",tt + 1);
    return 0;
}

2.2.2、vector优化

const int N = 1e6 + 10;

int n;
// nlogn
int main(){

    cin >> n;

    vector<int> arr(n);

    for(int i = 0;i < n;i++){
        cin >> arr[i];
    }
    vector<int> stk;
    //模拟堆栈
    stk.push_back(arr[0]);

    for(int i = 1; i < n;i++){
        if(arr[i] > stk.back()){
            stk.push_back(arr[i]);
        }else{
            *lower_bound(stk.begin(),stk.end(),arr[i]) = arr[i];
        }
    }

    cout << stk.size() << endl;
    return 0;
}

2.3、最长公共子序列

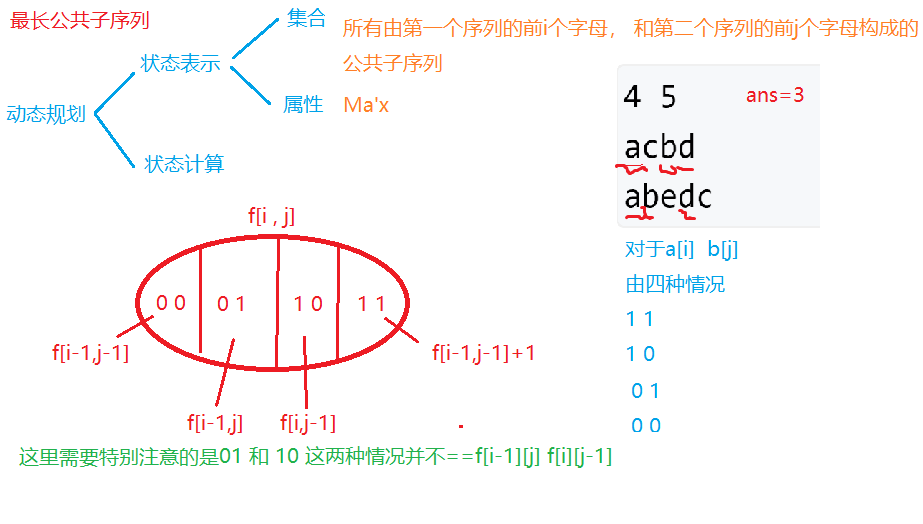
const int N = 1010;
int n,m;
char a[N], b[N];
int f[N][N];
int main(){

    scanf("%d%d",&n,&m);
    scanf("%s%s",a+1,b+1);

    for(int i = 1;i <= n ;i++){
        for(int j = 1; j <= m;j++){
            f[i][j] = max(f[i-1][j] , f[i][j-1]);
            if(a[i] == b[j]){
                f[i][j] = max(f[i][j], d[i-1][j-1] + 1);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

2.4、最短编辑距离-a-b

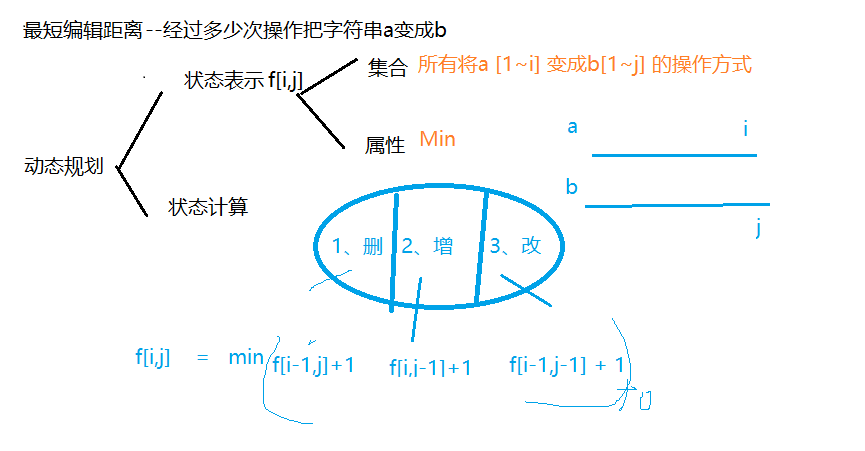
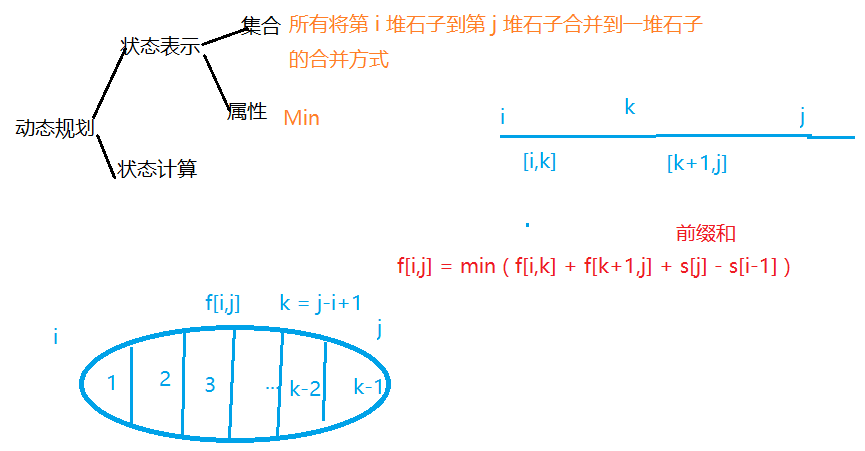
三、区间DP

石头合并–矩阵相乘

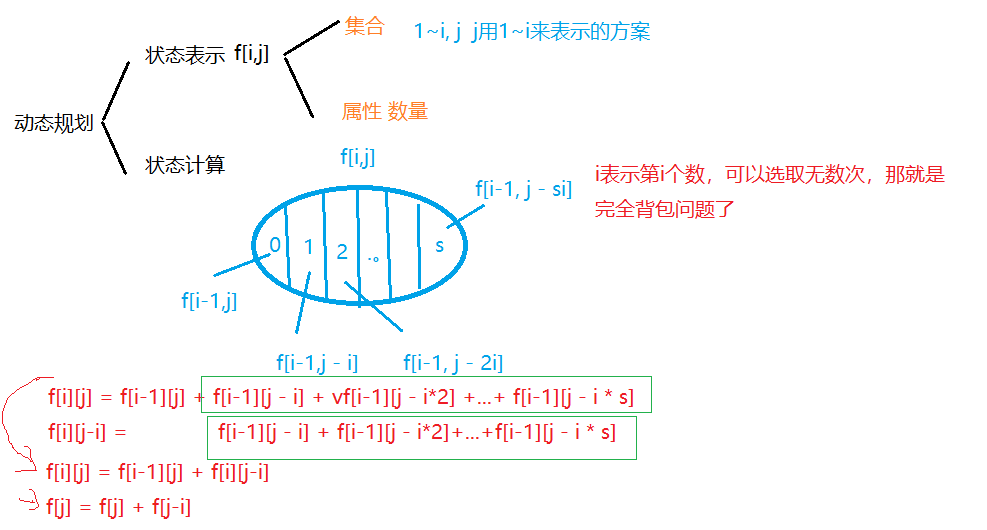
四、计数类DP

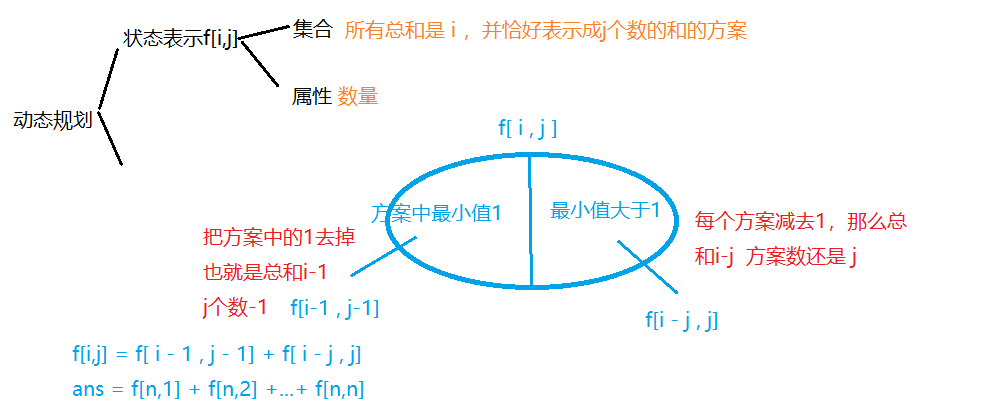
整数划分

2