第一章 动态规划
从集合角度分析DP问题
动态规划
状态表示
- 集合
- 属性
状态计算
- 集合划分(Max /Min / 数量)
原则:不重,不漏,其中不重复不一定都必须满足,而不漏在求Max / Min / 数量时都要满足。
求数量时要求不重复,但在求Max/Min时可以不满足
求Max / Min 时重复了并不会使得答案发生改变
数字三角形模型
- 摘花生
本题求所有走到左下角方案中的最大值,因此可以使用DP来解决
二维平面,从左上角到右下角
记录坐标需要两个参数
状态表示:
集合:$f[i,j]$表示从(1,1)走到(i,j)这个点的所有方案
属性:花生数的最大值
状态计算:
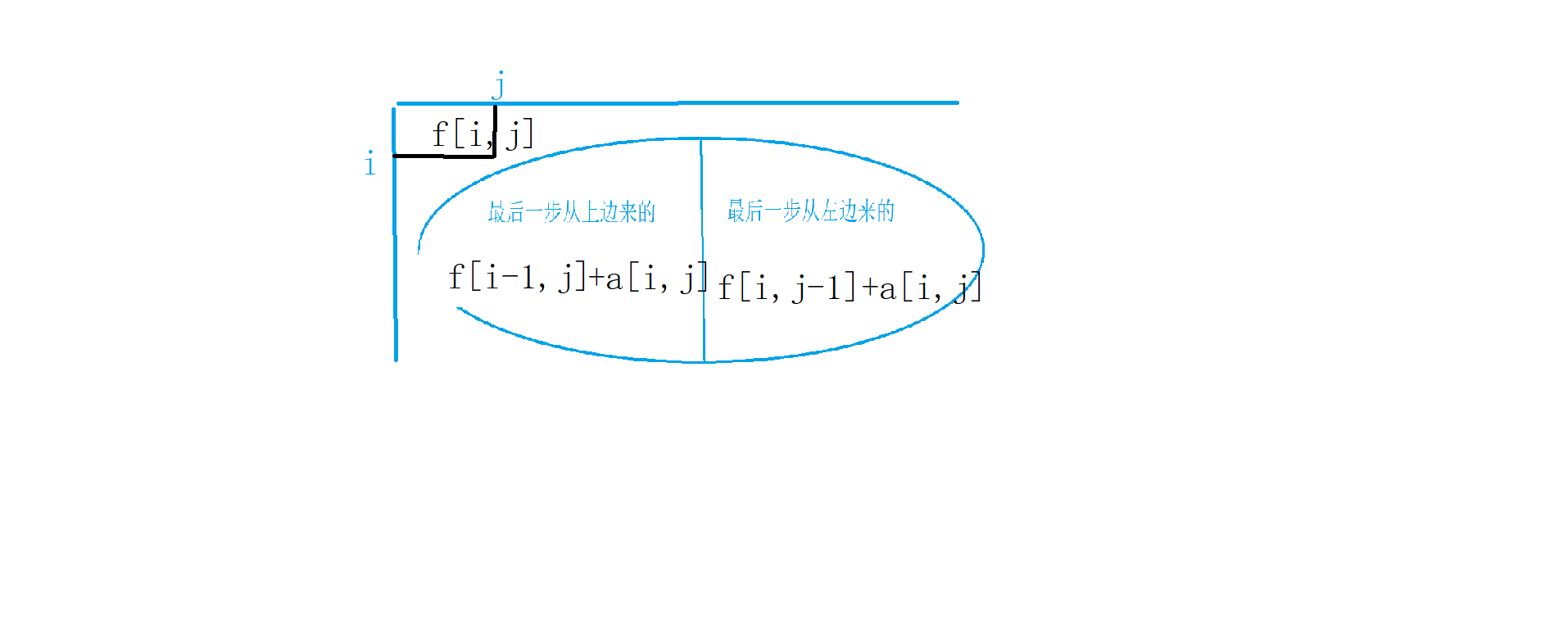
一般的集合划分依据:按最后一步的选法划分,先求子集花生数,再取子集中最大的一类。即此题可以按最后一步是从上边来的还是从左边来的进行划分,所有从(1,1)走到(i,j)划分为:从(1,1)走到(i-1,j)再走到(i,j)以及从(1,1)走到(i,j-1)再走到(i,j)的所有方案。
#include<iostream>
#include<cstring>
using namespace std;
const int N = 110;
int n,m;
int w[N][N];
int f[N][N];//求最大初始化(是0,花生数都是正数,可以被更新);
int main()
{
int T;
cin >> T;
while(T--)
{
cin >> n >> m;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=m;j++)
cin >> w[i][j];
//后一个状态由前一个状态所得出(拓扑序)
//从前往后枚举,线性DP按下标的一种顺序。
for(int i = 1;i<=n;i++)
for(int j = 1;j<=m;j++)
f[i][j] = max(f[i][j-1],f[i-1][j])+w[i][j];
cout << f[n][m] << endl;
}
return 0;
}
- 最低通行费
分析题意,必须在$n*n$个方格中穿越 $(2n - 1)$次
说明和摘花生一题类似,只能往右边或往下边走,这样有且只有
$(2n-1)$个格子,集合相同,属性改成求最小,用摘花生的解法。
//求最小要初始化INF
#include<iostream>
#include<cstring>
using namespace std;
const int N = 110,INF = 0x3f3f3f3f;
int n;
int w[N][N];
int f[N][N];
int main()
{
cin >> n;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
cin >> w[i][j];
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
{
/*
由于f[0][i],f[j][0]都是0,第一行第一列只能
缴纳当前的格子费用,防止取最小时被更新成0.
*/
if(i == 1 && j == 1)f[i][j] = w[i][j];
else
{
//初始化
f[i][j] = INF;
if(i>1)f[i][j] = min(f[i][j],f[i-1][j] + w[i][j]);
if(j>1)f[i][j] = min(f[i][j],f[i][j-1] + w[i][j]);
}
}
cout << f[n][n];
return 0;
}
- 方格取数
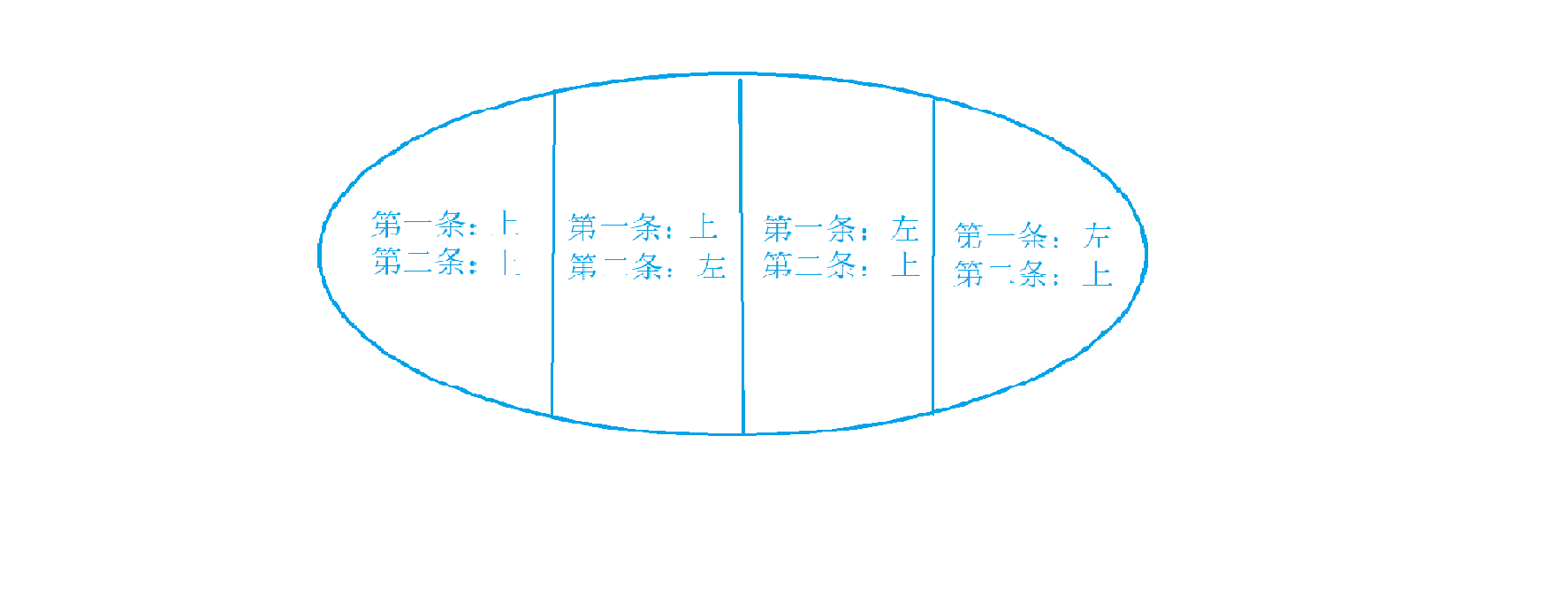
此题与摘花生不同的是从右上角走到左下角走两次,不能走相同的格子(走过一遍数变成0了,再走一次没意义),此时我们需要两个当前坐标 $f[x1,y1,x2,y2]$ 表示从$(1,1)$走到$(x1, y1),(x2, y2)$的所有方案的集合,但由于两个方向是同时走的,相遇时:
$x1 == x2, y1 == y2$ . 且 总步数 $k = = (x1 + y1) == (x2 + y2)$ ,各走一次$k = 2$,走到终点时$k = n + n$,此时状态表示可以写成$f[k,x1,x2]$。表示从$(1,1)$走到$(i1,k - i1),(i2,k - i2)$的路径的最大值。
重合时:$+w[i1,j1]$ 不重合时:$+w[i1,j1] + w[i2,j2]$
集合划分:(按找两种方案最后一步的方向划分为2 * 2 4种不漏不重的方案)
#include<iostream>
#include<cstring>
using namespace std;
const int N = 15;
int n;
int w[N][N];
int f[N*2][N][N];//不走路就不取数 0
int main()
{
int a,b,c;
cin >> n;
while(cin >> a >> b >> c,a||b||c)w[a][b] = c;
for(int k = 2;k<=n+n;k++)
for(int i1 = 1;i1<=n;i1++)
for(int i2 = 1;i2<=n;i2++)
{
int j1 = k-i1,j2 = k-i2;// k = i1+j1 = i2 + j2
if(j2>=1&&j2<=n&&j1>=1&&j1<=n)
{
int t = w[i1][j1];
if(i1 != i2)t +=w[i2][j2]; //重合只加一次,
int &x = f[k][i1][i2];
x = max(x,f[k-1][i1-1][i2-1]+t);//上一步,对第一条第二条路线枚举方向
x = max(x,f[k-1][i1][i2-1]+t);
x = max(x,f[k-1][i1-1][i2]+t);
x = max(x,f[k-1][i1][i2]+t);
}
}
cout << f[n+n][n][n];
return 0;
}
摘花生终极版:k取方格数(k <= 10)
(最小费用流…不会,先不写)
- 传纸条
最长上升子序列模型
- 怪盗基德的滑翔翼
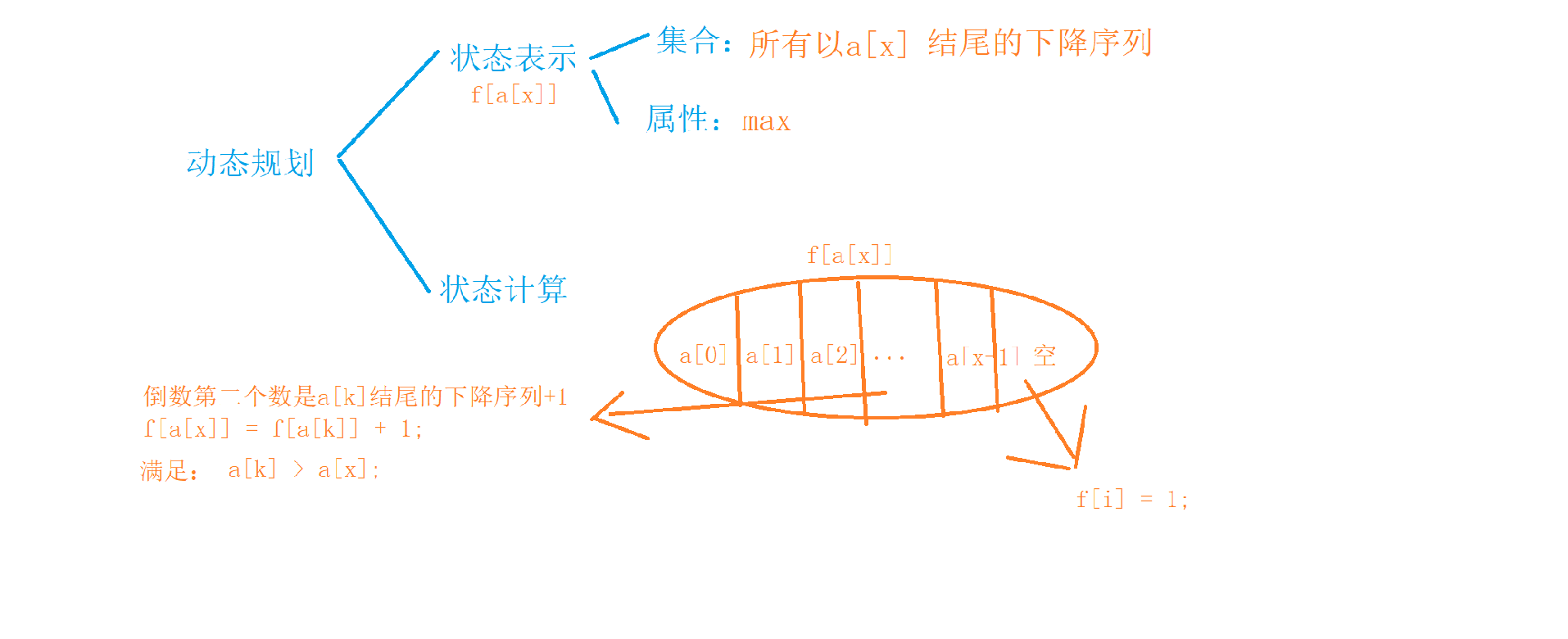
题意如下:找到数组中最长的严格下降区间,在所有的区间中取到长度最长的那一个,引导往DP集合的角度来解决问题,这里的楼房高度是用以为数组表示的,状态表示也用一维 f [ i ] 即可枚举所有集合,表示的是所有以 i 结尾的严格下降序列。
但是方向可正可负,因此需要从左右两个方向分别求一边最长的下降序列(当然反着看是上升的)。
//双向LIS
#include<iostream>
#include<cstring>
using namespace std;
const int N = 110;
int a[N],f[N];
int n;
int main()
{
int T;
cin >> T;
while(T--)
{
cin >> n;
int res = 0;
for(int i =1;i<=n;i++)cin >> a[i];
//正向
for(int i = 1;i<=n;i++)
{
f[i] =1 ;//前面没有比自己小的
for(int j = 1;j<i;j++)
{
if(a[j]<a[i])
{
f[i] = max(f[i],f[j]+1);
}
}
res = max(res,f[i]);
}
memset(f,0,sizeof f);
//反向
for(int i = n;i>=1;i--)
{
f[i] = 1;
for(int j = n;j>i;j--)
{
if(a[j] <a[i])
{
f[i] = max(f[i],f[j]+1);
}
}
res = max(res,f[i]);
}
cout << res << endl;
}
return 0;
}
- 登山
(看这题目滴名字h)能浏览最多的景点意味着找到所有区间中 连续的最长的上升区间 + 1 + 最长的下降区间(左右独立,左边最大+右边最大 = 最大)
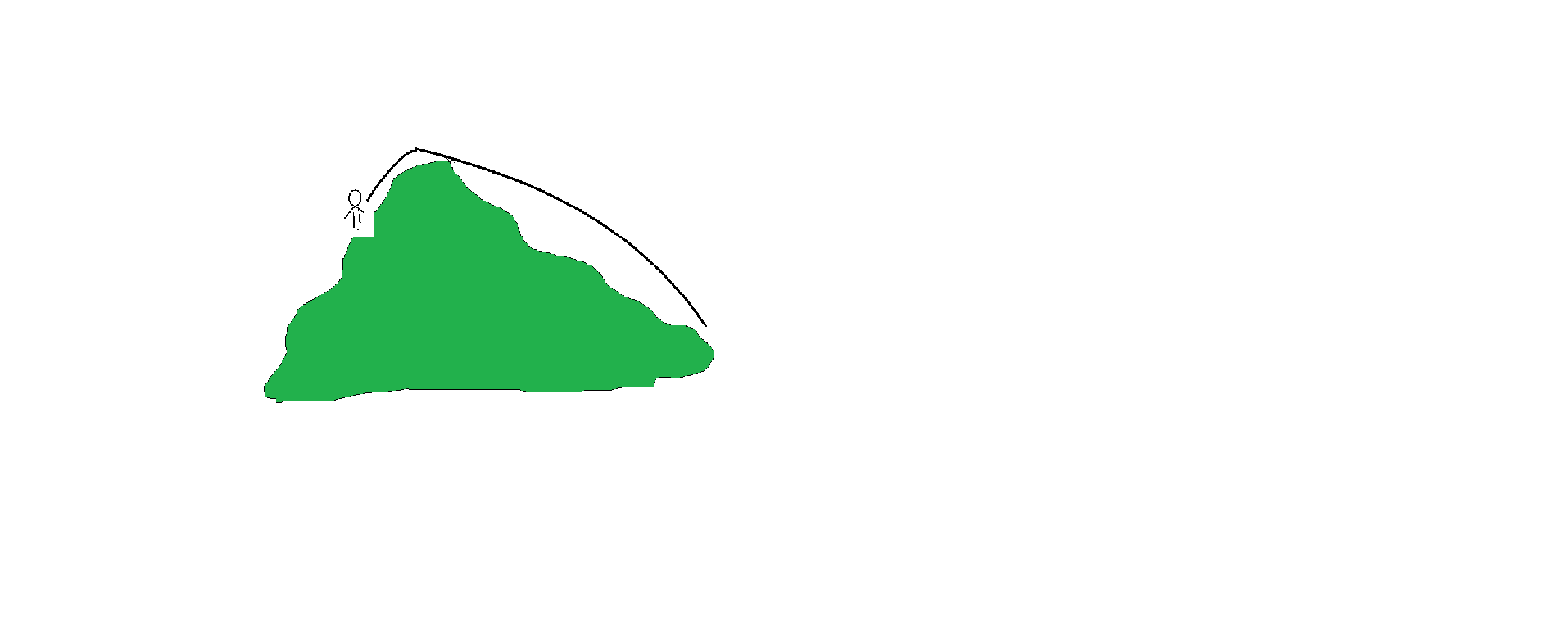
与怪盗基德的滑翔翼题类似,也都是一维,都是找出以i为分界点的最长序列,不同的是这里的a[i]作为顶点,可以先枚举左边的最大,再枚举右边的最大+预处理的左边的最大-重复计算的顶点,或反过来先枚举右边的也可以。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 1010;
int n,h[N],f[N],g[N];
int main()
{
int res = 0;
cin >> n;
for(int i = 1;i<=n;i++)cin >> h[i];
for(int i = 1;i<=n;i++)
{
f[i] = 1;
for(int j = 1;j<i;j++)
{
if(h[j]<h[i])
{
f[i] = max(f[i],f[j]+1);
}
}
res = max(res,f[i]);
}
for(int i = n;i>=1;i--)
{
g[i] = 1;
for(int j = n;j>i;j--)
{
if(h[j]<h[i])
{
g[i] = max(g[i],g[j]+1);
}
}
res = max(res,f[i]+g[i]-1); //顶点重复计算了
}
cout << res << endl;
return 0;
}
- 合唱队形
这题和登山互补,先找出最长的上升+顶点+最长的下降区间,总长度 减去 找出的区间长度就是答案

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 110;
int n,h[N],f[N],g[N];
int main()
{
cin >> n;
int res= 0;
for(int i =1 ;i<=n;i++)cin >> h[i];
for(int i = 1;i<=n;i++)
{
f[i] = 1;
for(int j = 1;j<i;j++)
{
if(h[i]>h[j])
{
f[i] = max(f[i],f[j]+1);
}
}
res = max(res,f[i]);
}
for(int i = n;i>=1;i--)
{
g[i] = 1;
for(int j = n;j>i;j--)
{
if(h[i]>h[j])
{
g[i] = max(g[i],g[j]+1);
}
}
res = max(res,g[i]+f[i]-1);
}
cout << n-res << endl;
return 0;
}
-
友好城市
-
最大上升子序列和
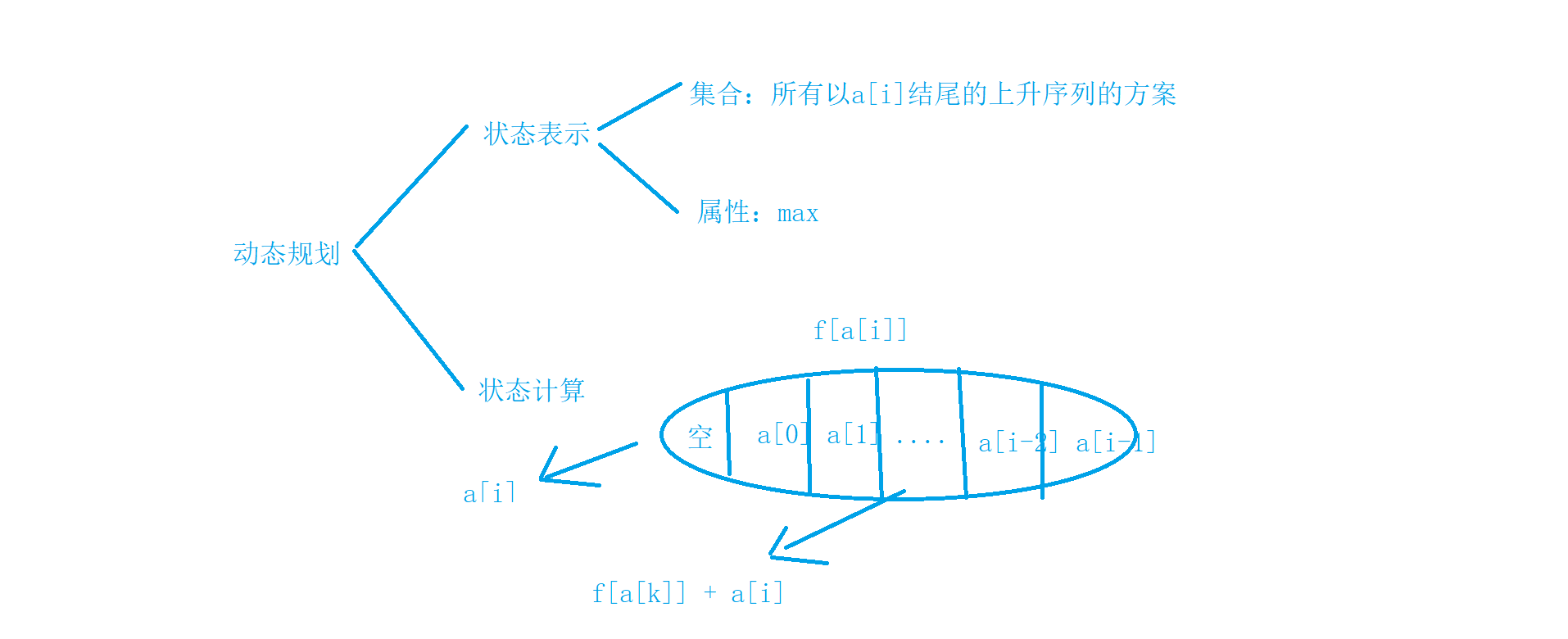
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 1010;
int n,h[N],f[N];
int main()
{
cin >> n;
int res = 0;
for(int i =1 ;i<=n;i++)cin >> h[i];
for(int i =1;i<=n;i++)
{
f[i] = h[i];
for(int j =1;j<i;j++)
{
if(h[i]>h[j])
{
f[i] = max(f[i],f[j]+h[i]);
}
}
res = max(res,f[i]);
}
cout << res << endl;
return 0;
}
- 拦截导弹
- 导弹防御系统
- 最长公共上升子序列
背包模型
01背包问题:选的话只能选一次,且选完后体积不能超,即 需要满足 j > w[i] 。
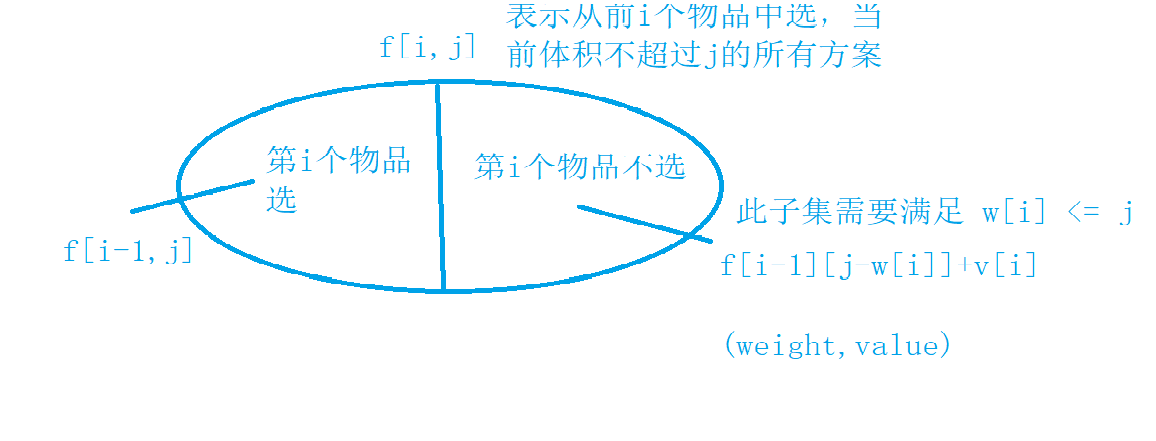
f[i][j] = max(f[i-1][j],f[i-1][j-w[i]] + v[i]);
#include<iostream>
using namespace std;
const int N = 1010;
int n,m;
int w[N],v[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)cin >> w[i] >> v[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
{
if(j >= w[i])f[i][j] = max(f[i-1][j],f[i-1][j-w[i]] + v[i]);
else f[i][j] = f[i-1][j];
}
cout << f[n][m] << endl;
return 0;
}
完全背包问题:选的话可以选无限次,但选完后体积不能超,即 需要满足 j > k * w[i] ,k表示第i个物品选的个数
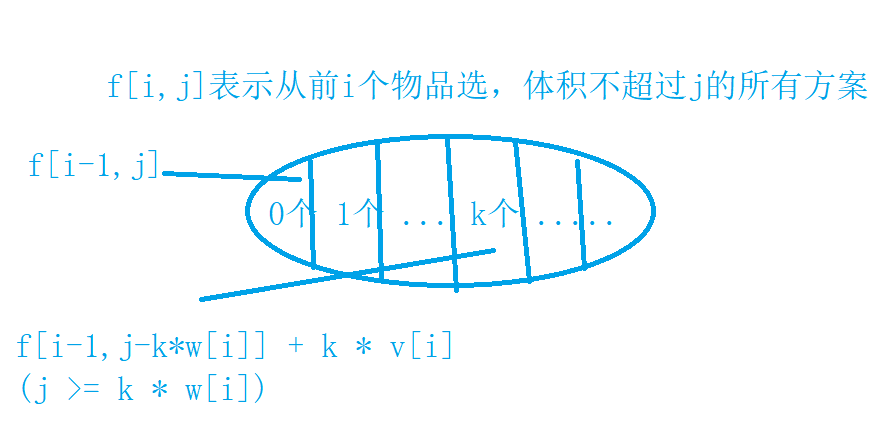
超时警告:
f[i][j] = max(f[i-1][j-w[i] * k] + v[i] * k);
#include<iostream>
using namespace std;
const int N = 1010;
int n,m;
int v[N],w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)cin >> w[i] >> v[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
for(int k = 0; k <= j / w[i]; k++)
f[i][j] = max(f[i-1][j],f[i-1][j-k * w[i]] + k * v[i]);
cout << f[n][m] << endl;
return 0;
}
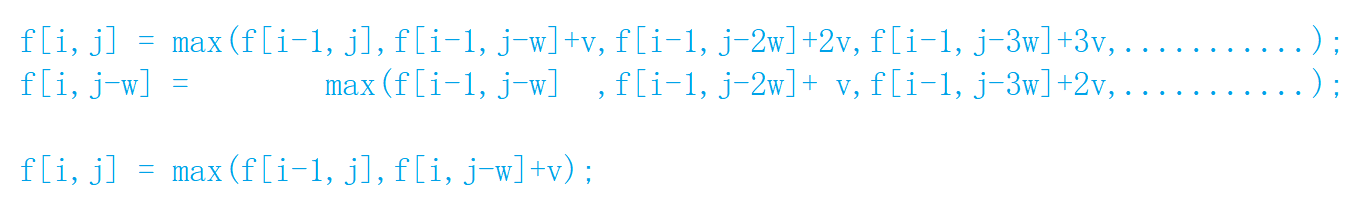
0 1: f[i][j] = max(f[i-1][j],f[i-1][j-w[i]] + v[i]);
完全: f[i][j] = max(f[i-1][j],f[i][j-w[i]] + v[i]);
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n,m;
int v[N],w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n ; i++)cin>>v[i]>>w[i];
//枚举物品
for(int i = 1;i<=n;i++)
//枚举体积
for(int j = 0;j <= m ; j ++)
{
//集合划分求最大
f[i][j] = f[i-1][j];
if(j>=v[i])f[i][j] = max(f[i-1][j],f[i][j-v[i]]+w[i]);
}
cout<<f[n][m];
return 0;
}
多重背包问题 I: 选的话可以选 s[i] 次,但选完后体积不能超,即 需要满足 j > k * w[i] ,k表示第i个物品选的个数。
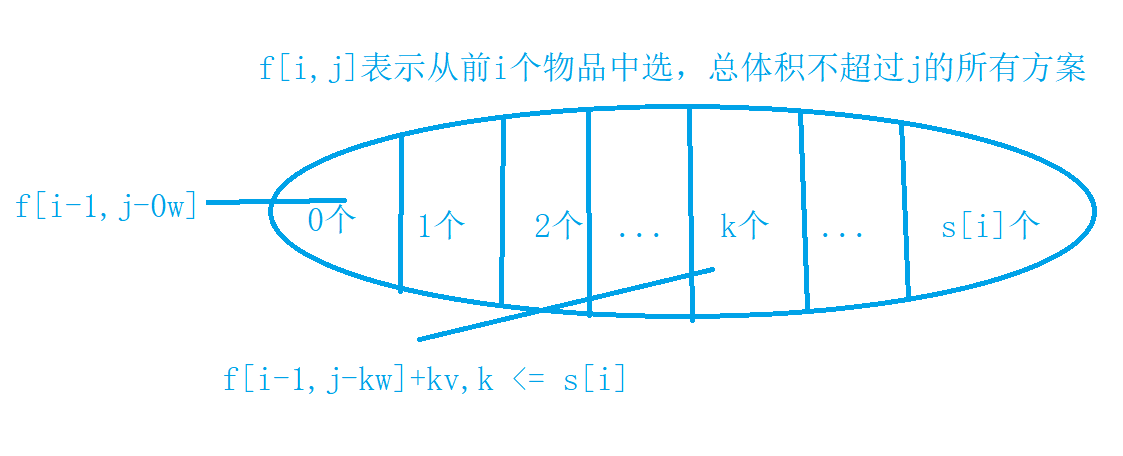
f[i][j] = max(f[i-1][j-w[i] * k] + v[i] * k);k <= s[i] && j >= k*w[i];
#include<iostream>
using namespace std;
const int N = 110;
int n,V;
int a[N];
int f[N][N];
int s[N];
int w[N],v[N];
int main()
{
cin >> n >> V;
for(int i = 1; i <= n; i++)cin >> w[i] >> v[i] >>s[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= V; j++)
for(int k = 0;k <= s[i];k++)
{
if(j>=k*w[i])f[i][j] = max(f[i][j],f[i-1][j-k*w[i]]+k*v[i]);
}
cout << f[n][V] << endl;
return 0;
}
多重背包问题II : 选的话可以选 s[i] 次,但选完后体积不能超,即 需要满足 j > k * w[i] ,k表示第i个物品选的个数。数据加强版 (本题考查多重背包的二进制优化方法。)
为啥用二进制优化?
0<N≤10000<N≤1000
0<V≤20000<V≤2000
0<vi,wi,si≤2000
f[i][j] = max(f[i-1][j-w[i] * k] + v[i] * k)
三重循环会超时滴
既然会超时,能不能借鉴完全背包问题的优化来考虑呢
从状态转移方程出发
f[i][j] = max(f[i-1][j-w[i] * k] + v[i] * k,....f[i-1][j-w[i] * s[i]] + s[i] * v)
f[i][j-w]=max(f[i-1][j-w[i] * (k+1)] + v[i] * k,..,f[i-1][j-w[i]*(s[i]+1)]+s[i]*v);
可见这里的f[i][j-w]要求得最大值里面多了一项f[i-1][j-w[i]*(s[i]+1)]+s[i]*v。
而已知两个集合的最大值要求其中一个集合的最大值是行不通的
这里提示用二进制来优化
先来考虑一个q = 2的等比数列
a1 = 1 ,a2 = 2 ,a3 = 4 ,a4 = 8 ,a5 = 16 ,... ,ak = 512;
可以凑出来的整数:
仅用a1 0~1
仅用a1,a2 0~1 ∪ 2~3 = 0~3
仅用a1,a2,a3 0~3 ∪ 4~7 = 0~7
仅用a1,a2,a3,a4 0~7 ∪ 8~15= 0~15
.....
仅用a1,a2,a3,....ak 0~a1+a2+a3+...ak = 0~2^(k-1) - 1
再来考虑一个一般的数s[i]
s[i] = a1 + a2 + .. + ax + s[i] - (2^(x-1)-1)
再来看转移方程:
f[i][j] = max(f[i-1][j-w[i] * k] + v[i] * k,....f[i-1][j-w[i] * s[i]] + s[i] * v)
这里我们对s[i]进行1+1+1+1...+1 = s[i]一共s[i]次操作
倘若使用公比是2的等比数列呢?
只需 log(s[i])上取整+1 次
将一个n次运算降至 log(n) 的01背包问题
就是所谓的二进制优化了
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 12010, M = 2010;
int n, m;
int v[N], w[N];
int f[M];
int main()
{
cin >> n >> m;
int cnt = 0;
for (int i = 1; i <= n; i ++ )
{
int a, b, s;
cin >> a >> b >> s;
int k = 1;
while (k <= s)
{
cnt ++ ;
w[cnt] = a * k;
v[cnt] = b * k;
s -= k;
k *= 2;
}
if (s > 0)
{
cnt ++ ;
w[cnt] = a * s;
v[cnt] = b * s;
}
}
n = cnt;
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= w[i]; j -- )
f[j] = max(f[j], f[j - w[i]] + v[i]);
cout << f[m] << endl;
return 0;
}
- 采药
这题时间就是背包体积,价值还是价值,在一定时间内,每路过一株药草,要么摘,要么不摘,摘只有眼前的一株,可见这题是01背包问题
#include<iostream>
using namespace std;
const int N = 1010;
int f[N][N],v[N],w[N],n,m;
int main()
{
cin >> n >> m;
for(int i = 1;i<=m;i++)cin >> w[i] >> v[i];
for(int i = 1;i<=m;i++)
for(int j = 0;j<=n;j++)
{
if(j < w[i])
{
f[i][j] = f[i-1][j];
}
else
{
f[i][j] = max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
}
}
cout << f[m][n] << endl;
return 0;
}
- 装箱问题
题目要求使得箱子的剩余空间最小,反之我们选取的物品总体积达到最大即可,而每种物品只有1件,可选可不选,这是一个01背包问题啊
#include <iostream>
using namespace std;
int V,n;
int f[20020];
int main(){
int v;
cin>>V>>n;
for(int i=0;i<n;i++){
cin>>v;
for(int j =V;j>=v;j--)
f[j] =max(f[j],f[j-v]+v);
}
cout<<V-f[V]<<endl;
return 0;
}
- 宠物精灵之收服
- 数字组合

#include<iostream>
using namespace std;
const int N = 10010;
int n,m;
int a[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)cin >> a[i];
for(int i = 0; i <= n; i++)f[i][0] = 1;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j <= m; j++)
{
f[i][j] = f[i-1][j] + f[i-1][j-a[i]];
}
}
cout << f[n][m] << endl;
return 0;
}
- 买书

#include<iostream>
using namespace std;
const int N = 1010;
int f[N][N];
int a[5] = {0,10,20,50,100};
int n;
int main()
{
cin >> n;
for(int i = 0; i <= 4; i++) f[i][0] = 1;
for(int i = 1; i<= 4;i++)
{
for(int j = 0 ; j<= n;j++)
{
f[i][j]=f[i-1][j];
if(j>=a[i]) f[i][j]+=f[i][j-a[i]];// 注意条件
}
}
cout << f[4][n] << endl;
return 0;
}
- 货币系统
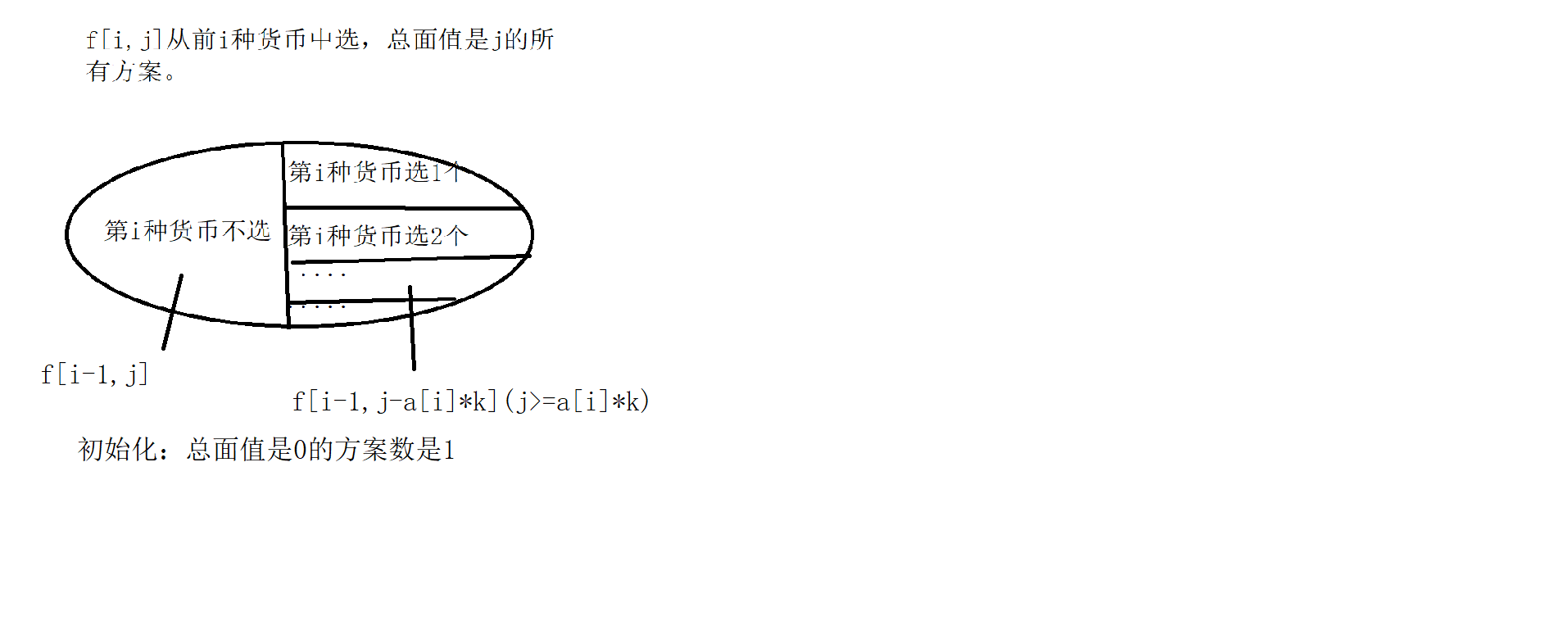
#include<iostream>
using namespace std;
const int N = 16,M = 3010;
long long f[N][M];
int n,m,t;
int a[N];
int main()
{
cin >> n >> m;
int x;
while(cin >> x) a[++t] = x;
for(int i = 0; i <= n; i++)f[i][0] = 1;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j <= m; j++)
{
f[i][j] = f[i-1][j];
for(int k = 1; k * a[i] <= j; k ++)
{
f[i][j] += f[i-1][j-k * a[i]];
}
}
}
cout << f[n][m] << endl;
return 0;
}
- 多重背包问题III
- 庆功会

#include<iostream>
using namespace std;
const int N = 510,M = 6010;
int f[N][M];
int n,m;
int v[N],w[N],s[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)cin >> v[i] >> w[i] >> s[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
for(int k = 0;k <= s[i];k++)
{
if(j>=k*v[i])f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
cout << f[n][m] << endl;
return 0;
}
- 混合背包问题
- 二维费用的背包问题
- 潜水员
- 机器分配
- 开心的金明
- 有依赖的背包问题
- 背包问题求方案数
- 背包问题求具体方案
- 能量石
- 金明的预算方案
状态机模型
- 大盗阿福
- 股票买卖IV
- 股票买卖V
- 设计密码
- 修复DNA
状态压缩DP
- 骑士
- 玉米田
- 炮兵阵地
- 愤怒的小鸟
- 宝藏
区间DP
- 环形石子合并
- 能量项链
- 加分二叉树
- 凸多边形的划分
- 棋盘分割
树形DP
- 树的最长路径
- 树的中心
- 数字转换
- 二叉苹果树
- 战略游戏
- 皇宫看守
数位DP
- 度的数量
- 数字游戏
- Windy数
- 数字游戏II
- 不要62
- 恨7不成妻
单调队列优化DP
- 最大子序和
- 修剪草坪
- 旅行问题
- 烽火传递
- 绿色通道
- 理想的正方形
斜率优化DP
-
任务安排1
-
任务安排2
-
任务安排3
-
运输小猫


赞一个 !加油 !
谢谢emm,尽力趴,背包里面要结合单调队列单调栈贪心什么的,我又回头取补了,可能一星期更不完了emm(太弱了我)