A. 马林和照片拍摄
每次测试的时间限制1秒
每次测试的内存限制256兆字节
输入标准输入
输出标准输出
今天,马林参加了一个COSPLAY展览,并准备拍集体照!
为了拍集体照,cosplay们形成一条横线。如果对于每条至少有2名cosplay者的连续段,男性的数量不超过女性的数量(很明显),那么这张合影就被认为是美丽的。
目前,这条线有n个coser,可以用一个二进制字符串s来描述。如果si=0,第i个coser就是男性,如果si=1,就是女性。为了保证队伍的美观,你可以邀请一些额外的coser(可能是零)在任何位置加入队伍。你不能从队伍中删除任何cosplayer。
Marin想知道你需要邀请的coser的最少数量,以便所有coser的合影都是美丽的。她自己无法做到这一点,所以她请求你的帮助。你能帮助她吗?
输入
第一行包含一个整数t(1≤t≤103)--测试案例的数量。
每个测试案例的第一行包含一个正整数n(1≤n≤100)--初始行中cosplay的数量。
每个测试案例的第二行包含一个长度为n的二进制字符串s--描述已经在队伍中的cosplayer。字符串的每个字符要么是0,描述男性,要么是1,描述女性。
请注意,对n的总和没有限制。
输出
对于每个测试案例,打印出你需要邀请的最小cosplay者人数,以便所有cosplay者的合影都是美丽的。
注意
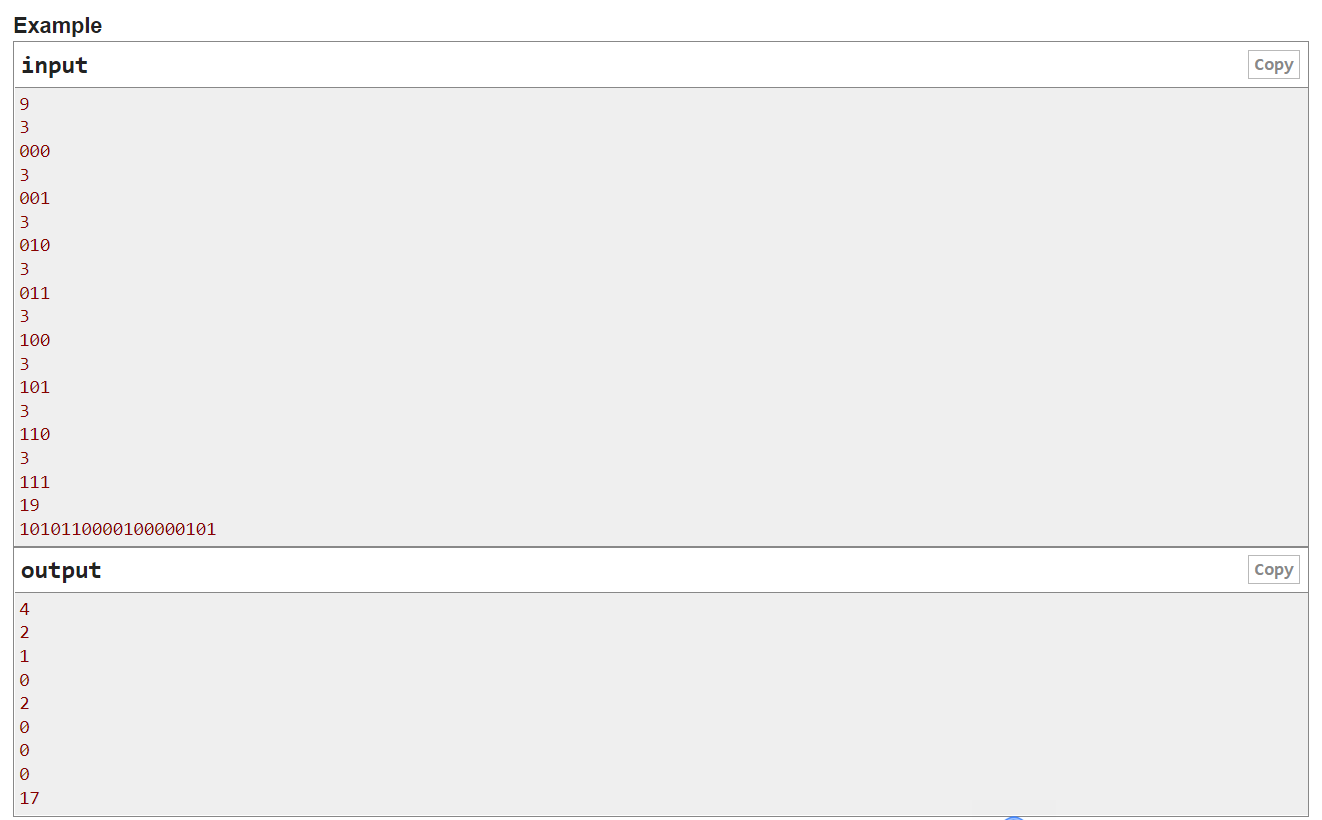
在第一个测试案例中,对于每一对相邻的coser,你可以邀请两名女coser站在他们中间。然后,000→0110110。
在第三个测试案例中,你可以邀请一个女coser站在第二个coser的旁边。然后,010→0110。

#include<iostream>
using namespace std;
int main()
{
int t;
cin >> t;
while(t --)
{
int cnt = 0;
int n;
cin >> n;
string s;
cin >> s;
for(int i = 0; i < n; i ++)
{
if(s[i] == '0' && s[i + 1] == '0') cnt += 2;
if(s[i] == '0' && s[i + 1] == '1' && s[i + 2] == '0') cnt ++;
}
cout << cnt << endl;
}
}
B. 马林和反共的排列组合
每次测试的时间限制1秒
每次测试的内存限制256兆字节
输入标准输入
输出标准输出
马林希望你能计算出漂亮的排列组合的数量。一个长度为n的美丽的排列组合是一个具有以下性质的排列组合。
gcd(1⋅p1,2⋅p2,...,n⋅pn)>1。
其中gcd是最大公除数。
遍历是一个由1到n的n个不同整数按任意顺序组成的数组。例如,[2,3,1,5,4]是一个排列组合,但[1,2,2]不是排列组合(2在数组中出现两次),[1,3,4]也不是排列组合(n=3但在数组中有4)。
输入
第一行包含一个整数t(1≤t≤103)--测试案例的数量。
每个测试用例包括一行,包含一个整数n(1≤n≤103)。
输出
对于每个测试案例,打印一个整数--美丽的排列组合的数量。因为答案可能非常大,请打印答案的模数998244353。
注意
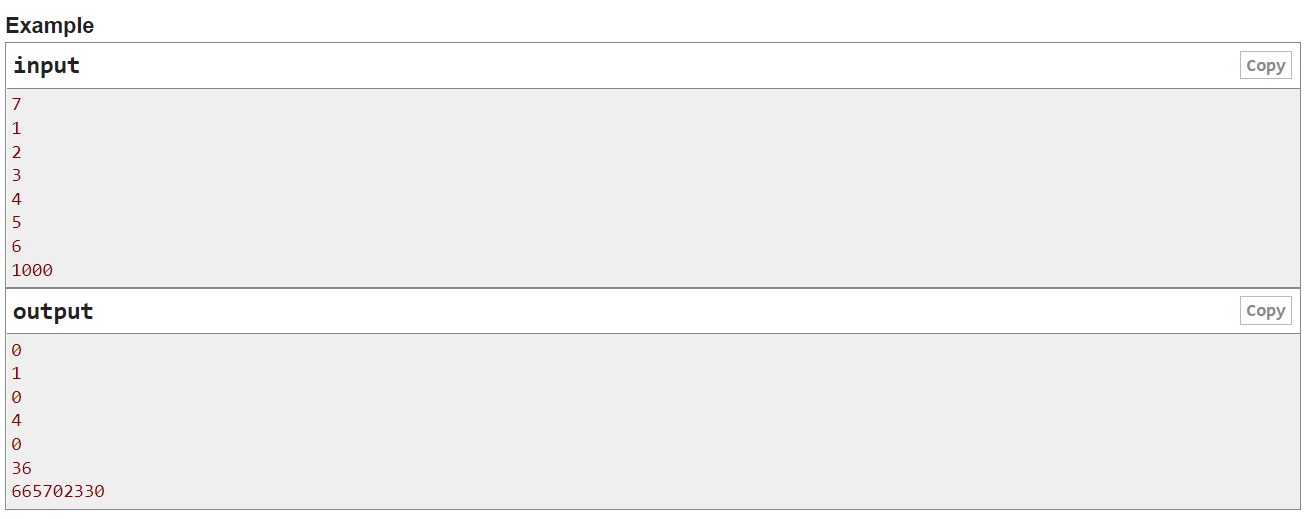
在第一个测试案例中,我们只有一个排列组合,即[1],但它并不漂亮,因为gcd(1⋅1)=1。
在第二个测试案例中,我们只有一个漂亮的排列组合,即[2,1],因为gcd(1⋅2,2⋅1)=2。

但是其实在1,2,3, 4序号匹配1, 2, 3, 4全排列的时候3是不可能作为最大公约数因为多3,和另一个不含因子为三的数有公因子三,所以随着n的变大所有三的因子的数是远远不足以支持作为公因子,所以2是最大公因子
#include<iostream>
using namespace std;
typedef long long ll;
ll mod = 998244353;
ll fac(ll n)
{
if(n == 1) return 1;
return (ll)(n * fac(n - 1)) % mod;
}
int main()
{
int t;
cin >> t;
while(t --)
{
ll n; cin>>n;
if(n%2==1) {cout<<'0'<< endl;continue;}
ll res = fac(n/2)*fac(n/2) % mod;
cout << res << endl;
}
return 0;
}
C. 神州与失落的排列组合
每次测试的时间限制1秒
每次测试的内存限制256兆字节
输入标准输入
输出标准输出
真珠非常喜欢排列组合! 今天,她从Juju那里借了一个排列组合p来玩。
一个互换式p的第i次循环移位是互换式上的一个变换,这样p=[p1,p2,...,pn]现在将变成p=[pn-i+1,...,pn,p1,p2,...,pn-i]。
让我们把互换的幂数定义为互换的前缀最大数组b中的独特元素的数量。前缀最大数组b是一个长度为n的数组,使得bi=max(p1,p2,...,pi)。例如,[1,2,5,4,6,3]的幂是4,因为b=[1,2,5,5,6,6],b中有4个不同元素。
不幸的是,信州已经失去了排列组合p! 她唯一记得的信息是一个数组c,其中ci是 permutation p的第(i-1)次循环移位的幂,她也不确定自己是否记得正确,所以她想知道自己的记忆是否足够好。
给出数组c,确定是否存在一个与c一致的互换p,你不必构建互换p。
一个排列组合是由任意顺序的1到n个不同的整数组成的阵列。例如,[2,3,1,5,4]是一个排列组合,但[1,2,2]不是排列组合(2在数组中出现两次),[1,3,4]也不是排列组合(n=3但数组中有4)。
输入
输入由多个测试案例组成。第一行包含一个整数t(1≤t≤5⋅103)--测试案例的数量。
每个测试用例的第一行包含一个整数n(1≤n≤105)。
每个测试用例的第二行包含n个整数c1,c2,...,cn(1≤ci≤n)。
保证所有测试用例的n之和不超过105。
输出
对于每个测试案例,如果存在一个满足数组c的排列组合p,则打印 "YES",否则打印 "NO"。
你可以在任何情况下输出 "YES "和 "NO"(例如,字符串 "yEs"、"yes"、"Yes "和 "YES "将被识别为一个积极的响应)。
注意
在第一个测试案例中,排列组合[1]满足阵列c的要求。
在第二个测试案例中,排列组合[2,1]满足数组c。
在第五个测试案例中,排列组合[5,1,2,4,6,3]满足数组c的要求。
p的第2个循环移位是[5,1,2,4,6,3]。它的幂是2,因为b=[5,5,5,5,6,6],有两个不同的元素--5和6。
p的第一个循环移动是[3,5,1,2,4,6]。因为b=[3,5,5,5,5,6],所以它的幂是3。
p的第二个循环移位是[6,3,5,1,2,4]。它的功率是1,因为b=[6,6,6,6,6]。
p的第三个循环移位是[4,6,3,5,1,2]。它的功率是2,因为b=[4,6,6,6,6]。
p的第四次循环移位是[2,4,6,3,5,1]。它的功率是3,因为b=[2,4,6,6,6]。
p的第五次循环移动是[1,2,4,6,3,5]。它的功率是4,因为b=[1,2,4,6,6,6]。
因此,c=[2,3,1,2,3,4]。
在第三、第四和第六个测试案例中,我们可以证明没有满足数组c的互换。
其实C题主要难度首先在读题
题目的意思是p是n的全排列,但是神州这个人不记得p的排列了,根据每个c数组是否能构造出合法的p的排列
而c数组的意思是ci是ai - 1的第i - 1次循环位移的b[]的不同的数目
而下一个不好注意到的点是判重1因为只有n在最前面的位置的的一种情况
不可能再出现c[i] = 1的情况可以手动模拟一下就知道因为总共就五次移动


而因为i次的移动就和i + n的移动是一样的所以就是将1前面的数拼接到1后面一起判断就好
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int a[N];
void solve() {
int n;
cin >> n;
for (int i = 1; i <= n; i++)cin >> a[i];
if (count(a + 1, a + 1 + n, 1) != 1) { cout << "NO" << endl; return; }
vector<int>v, b;
for (int i = 1; i <= n; i++) {
if (a[i] == 1) {
for (int j = i; j <= n; j++)b.push_back(a[j]);
for (int x : v)b.push_back(x);
break;
}
else v.push_back(a[i]);
}
for (int i = 1; i < b.size(); i++) {
if (b[i] - b[i - 1] > 1) { cout << "NO" << endl; return; }
}
cout << "YES" << endl;
}
int main()
{
int t;
cin >> t;
while(t --)
{
solve();
}
return 0;
}

