1.最短路基本性质
如果图中不存在负权回路,则当算法结束以后,对于边(x,y)有 dis[y]≤dis[x]+w ,即 dis[y]−dis[x]≤w 成立。
2.差分约束系统

3.差分约束系统与最短路径

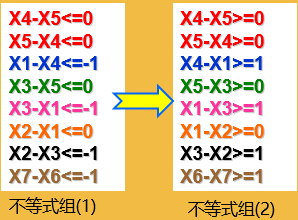
4.构图求解
4.1构图

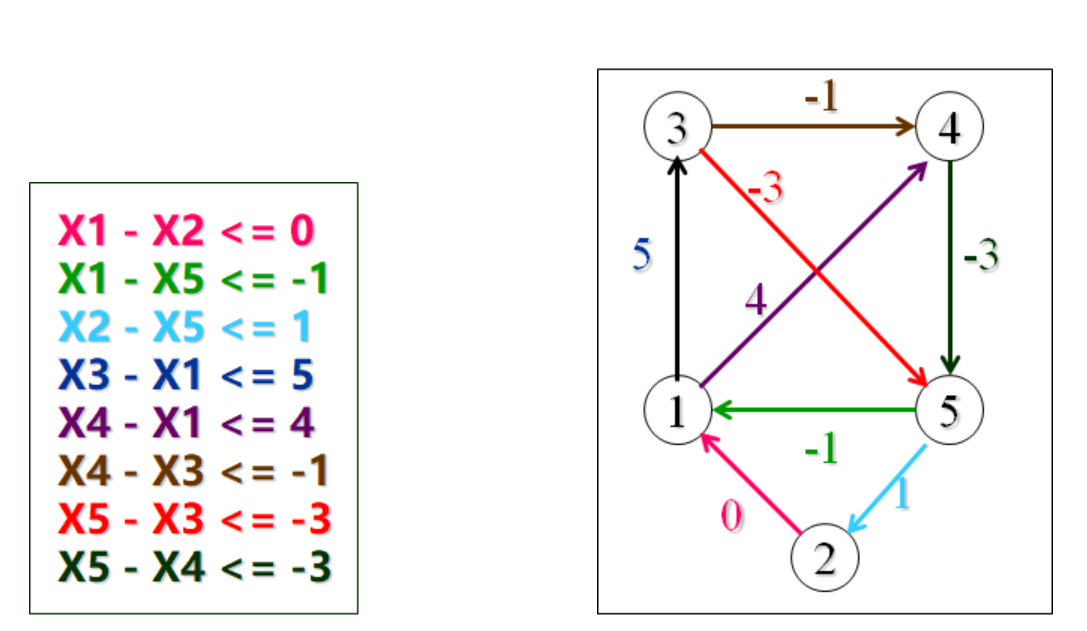
4.2求解

若存在负环,则不等式组一定矛盾。
即:不等式组无解 <-> 存在负环(最短路)/存在正环(最长路)
4.3增加源点
源点需要满足的条件:从源点出发,一定可以走到所有的边(不一定要走到所有的点,某个点走不到表示该点孤立,对应变量无限制,可任意取值).
从0号点可以走到任意点,则一定可以到达所有边。(反之,可以走到任意边不一定能到达任意点)

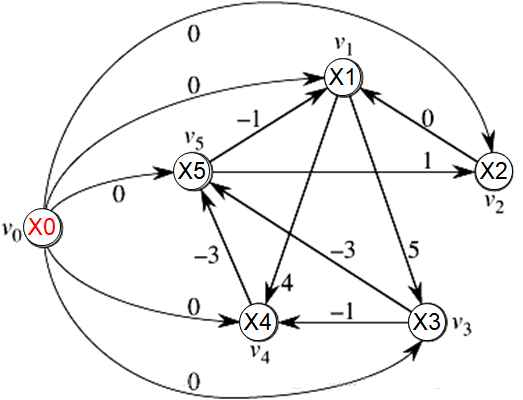

4.3解的存在性
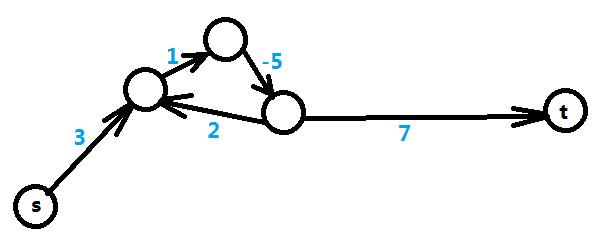
,先来看负权圈的情况,如图三-3-1,下图为5个变量5个不等式转化后的图,需要求得是X[t] - X[s]的最大值,可以转化成求s到t的最短路,但是路径中出现负权圈,则表示最短路无限小,即不存在最短路,那么在不等式上的表现即X[t] - X[s] <= T中的T无限小,得出的结论就是 X[t] - X[s]的最大值不存在
再来看另一种情况,即从起点s无法到达t的情况,如图,表明X[t]和X[s]之间并没有约束关系,这种情况下X[t] - X[s]的最大值是无限大,这就表明了X[t]和X[s]的取值有无限多种。
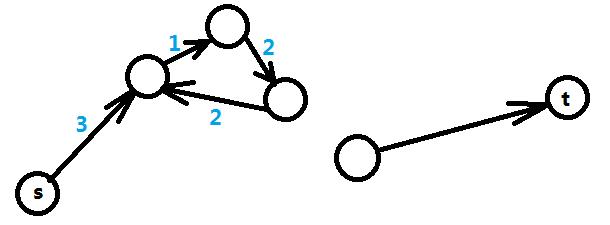
在实际问题中这两种情况会让你给出不同的输出。综上所述,差分约束系统的解有三种情况:1、有解;2、无解;3、无限多解;
附:提高课笔记

最长路 <-> 大于关系
最短路 <-> 小于关系
例题
1.线性约束
线性约束一般是在一维空间中给出一些变量(一般定义位置),然后告诉你某两个变量的约束关系,求两个变量a和b的差值的最大值或最小值。
acwing1169
像这类问题,N个人的位置在一条直线上呈线性排列,某两个人的位置满足某些约束条件,最后要求第一个人和最后一个人的最长可能距离,这种是最直白的差分约束问题,因为可以用距离作为变量列出不等式组,然后再转化成图求最短路。

#include<iostream>
#include<cstring>
using namespace std;
int n,k;
const int N=100010,M=300010;//3倍:第一种情况建两条边,源点到各个顶点连一条边
int h[N],e[M],ne[M],w[M],idx;
typedef long long LL;
int dist[N];
int q[N],cnt[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
bool spfa()
{
int hh=0,tt=1;
memset(dist,-0x3f,sizeof dist);
dist[0]=0;
q[0]=0;
st[0]=true;
while(hh != tt)
{
int t=q[--tt];
st[t]=false;
for(int i=h[t];~i;i=ne[i])
{
int j=e[i];
if(dist[j] < dist[t] + w[i])
{
dist[j] =dist[t] + w[i];
cnt[j]=cnt[t]+1;
if(cnt[j] >= n+1)//b包含源点
return true;
if(!st[j])
{
q[tt++]=j;
st[j]=true;
}
}
}
}
return false;
}
int main()
{
cin>>n>>k;
memset(h,-1,sizeof h);
while(k--)
{
int x,a,b;
cin>>x>>a>>b;
if(x == 1)
add(a,b,0),add(b,a,0);
else if(x == 2)
add(a,b,1);
else if(x == 3)
add(b,a,0);
else if(x == 4)
add(b,a,1);
else
add(a,b,0);
}
for(int i=1;i<=n;i++)//增加源点,确保可遍历到所有点(所有边)
add(0,i,1);
if(spfa())
puts("-1");
else
{
LL res=0;
for(int i=1;i<=n;i++)
res+=dist[i];
printf("%lld\n",res);
}
return 0;
}
2.区间约束
acwing364
用s[i]表示[1, i]这个区间至少有多少点能被选中,s[0]=0;
s(b) - s(a - 1) >= c 所以 * (-1)得 s(a - 1) - s(b) <= -c 条件一
根据题目s(i) - s(i - 1) >= 0 所以 s(i - 1) - s(i) <= 0 条件二
每个位置上至多有一个元素 s(i ) - s(i - 1) <= 1 条件三
为了避免a - 1 < 0 所以在建图的时候全部 a , b 也就是将所有的区间向右挪一位
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=50010,M=150010;
int h[N],e[M],ne[M],w[M],idx;
int n;
int dist[N];
int q[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void spfa()
{
memset(dist, -0x3f, sizeof dist);
dist[0] = 0;
st[0] = true;
int hh = 0, tt = 1;
q[0] = 0;
while (hh != tt)
{
int t = q[hh ++ ];
if (hh == N) hh = 0;
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (dist[j] < dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j])
{
q[tt++] = j;
if (tt == N) tt = 0;
st[j] = true;
}
}
}
}
}
int main()
{
cin>>n;
memset(h,-1,sizeof h);
for(int i=1;i<N;i++)
{
add(i - 1, i, 0);//确保可遍历到所有点(所有边)
add(i, i - 1, -1);
}
for(int i=0;i<n;i++)
{
int a,b,c;
cin>>a>>b>>c;
a++,b++;
add(a - 1, b, c);
}
spfa();
printf("%d\n", dist[50001]);
return 0;
}
acwing1170
求最大值,跑最短路
记第i头牛的位置为di
di+1>=di
i+1向i连一条权值为0的边
两头牛有好感
dj-di≤L;= L 即dj≤ di + L
i向j连一条权值为L的边
两头牛反感
dj-di>=D即di ≤dj-D
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010, M = 21010, INF = 0x3f3f3f3f;
int n, m1, m2;
int h[N], e[M], w[M], ne[M], idx;
int dist[N];
int q[N], cnt[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int spfa(int size)
{
int hh = 0, tt = 0;
memset(dist, 0x3f, sizeof dist);
memset(st, 0, sizeof st);
memset(cnt, 0, sizeof cnt);
for (int i = 1; i <= size; i ++ )//等价于建立超级源点,确保可遍历到所有点(所有边)
{
q[tt ++ ] = i;
st[i] = true;
}
dist[1]=0;
while (hh != tt)
{
int t = q[hh ++ ];
if (hh == N) hh = 0;
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return -1;
if (!st[j])
{
q[tt ++ ] = j;
if (tt == N) tt = 0;
st[j] = true;
}
}
}
}
if(dist[n] == INF)
return -2;
return dist[n];
}
int main()
{
scanf("%d%d%d", &n, &m1, &m2);
memset(h, -1, sizeof h);
for (int i = 1; i < n; i ++ ) add(i + 1, i, 0);
while (m1 -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
if (a > b) swap(a, b);
add(a, b, c);
}
while (m2 -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
if (a > b) swap(a, b);
add(b, a, -c);
}
// if (spfa(n)) puts("-1");
// else
// {
// spfa(1);
// if (dist[n] == INF) puts("-2");
// else printf("%d\n", dist[n]);
// }
printf("%d",spfa(n));
return 0;
}
3. 未知条件约束
未知条件约束是指在不等式的右边不一定是个常数,可能是个未知数,可以通过枚举这个未知数,然后对不等式转化成差分约束进行求解。
acwing393
num[i]: 代表i时刻的收银员人数。
r[i]代表i时候至少需要的收银员人数。
s[i]:代表0~i 这个时间段收银员的人数。(前缀和,让0 ~ 23 时刻转化为 1 ~ 24时刻。确保 s[0] = 0)
不等式:(图片来自,@xxh)

可以看出:通过0点就能遍历所有的边,符合差分约束的条件。
所有最后一种约束关系都有s[24]变量,但s[24]是我们求的答案,所以我们可以枚举 s[24] 的值,把它变成常量.采用枚举s[24]的值,将它变成一个定值。建立2条边:s[24] >= s[0] + c, s[0] >= s[24] - c。 这样我们就通过超级源点0点将s[24]的值变成定值。 (s[0] = 0)
#include <cstdio>
#include <cstring>
#include<iostream>
using namespace std;
const int N = 30, M = 100,INF = 0x3f3f3f3f;
int h[N], e[M], w[M], ne[M], idx;
int r[N], num[N];
int dist[N];
int q[N], cnt[N];
bool st[N];
int n;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool spfa(int x)
{
memset(h, -1, sizeof h), idx=0;//根据枚举的s24进行建图
for (int i = 1; i <= 24; i++)
{
add(i - 1, i, 0), add(i, i - 1, -num[i]);
if (i >= 8)
add(i - 8, i, r[i]);
else
add(i + 16, i, -x + r[i]);
}
//由于我们还需要设置枚举的s24为定值 创建 s24<=k s24 >= k
add(0, 24, x), add(24, 0, -x);
memset(dist, -0x3f, sizeof dist);//最小值求最长路
memset(cnt, 0, sizeof cnt);
memset(st, false, sizeof st);
int hh = 0, tt = 1;
dist[0] = 0;//从源点0可以遍历所有的边
q[0] = 0;
st[0] = true;
while (hh != tt)
{
int t = q[hh ++ ];
if (hh == N) hh = 0;
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (dist[j] < dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= 25) return false;
if (!st[j])
{
q[tt ++ ] = j;
if (tt == N) tt = 0;
st[j] = true;
}
}
}
}
return true;
}
int main()
{
int T;
scanf("%d", &T);
while (T--)
{
memset(num, 0, sizeof num);//num[i] 代表i时刻的人数
for (int i = 1; i <= 24; i++)
scanf("%d", &r[i]);
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
int t;
scanf("%d", &t);
num[t+1]++;
}
//枚举s24的值
bool flag = false;
for (int i = 1; i <= n; i++) //从小到大枚举
{
if (spfa(i))
{
printf("%d\n", dist[24]);
flag = true;
break;
}
}
if (!flag) printf("No Solution\n");
}
return 0;
}
二分优化:
我们通过枚举得到s[24]的值。答案是满足单调性的。当最少的人数满足时,比这个最少人数多的一定满足。那么我们就可以二分这个区间。答案区间为[0,n+1] n+1代表的是不合法的区间,因为当n个人都无法满足 ,那么答案就会跳到n+1,我们直接判断n+1即可。
#include <cstdio>
#include <cstring>
#include<iostream>
using namespace std;
const int N = 30, M = 100,INF = 0x3f3f3f3f;
int h[N], e[M], w[M], ne[M], idx;
int r[N], num[N];
int dist[N];
int q[N], cnt[N];
bool st[N];
int n;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool spfa(int x)
{
memset(h, -1, sizeof h), idx=0;//根据枚举的s24进行建图
for (int i = 1; i <= 24; i++)
{
add(i - 1, i, 0), add(i, i - 1, -num[i]);
if (i >= 8)
add(i - 8, i, r[i]);
else
add(i + 16, i, -x + r[i]);
}
//由于我们还需要设置枚举的s24为定值 创建 s24<=k s24 >= k
add(0, 24, x), add(24, 0, -x);
memset(dist, -0x3f, sizeof dist);//最小值求最长路
memset(cnt, 0, sizeof cnt);
memset(st, false, sizeof st);
int hh = 0, tt = 1;
dist[0] = 0;//从源点0可以遍历所有的边
q[0] = 0;
st[0] = true;
while (hh != tt)
{
int t = q[hh ++ ];
if (hh == N) hh = 0;
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (dist[j] < dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= 25) return false;
if (!st[j])
{
q[tt ++ ] = j;
if (tt == N) tt = 0;
st[j] = true;
}
}
}
}
return true;
}
int main()
{
int T;
scanf("%d", &T);
while (T--)
{
memset(num, 0, sizeof num);//num[i] 代表i时刻的人数
for (int i = 1; i <= 24; i++)
scanf("%d", &r[i]);
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
int t;
scanf("%d", &t);
num[t+1]++;
}
//枚举s24的值
int l=0,r=n+1;
while(l<r)
{
int mid=l+r>>1;
if(spfa(mid))
r=mid;
else
l=mid+1;
}
if(r == n+1)
printf("No Solution\n");
else
printf("%d\n", l);
}
return 0;
}


4.3求解中,算出了每个点的dis值,那x1,x2,x3是怎么求出的呢?是x1=dis[1],x2=dis[2],x3=dis[3]吗??
如果是x1=dis[1],那为什么上面4.3写的dis[2]=2,x2=1,两者不相等?
这分享爱了,tql
二助,tql