参考文章：https://blog.csdn.net/weixin_43723614/article/details/105060144

第一种情况：当n<=32时,阶乘值在int范围内

常用的两种思路有循环或者递归，代码分别如下：

循环：

#include <iostream>

using namespace std;

int main()
{
    int n,res=1;

    scanf("%d",&n);

    for(int i=2;i<=n;i++)
        res*=i;

    printf("%d",res);

    return 0;
}

递归:

#include <iostream>

using namespace std;

int res=1;

void fact(int n)
{
    if(n==1)
    {
        printf("%d",res);
        return;
    }
    res*=n;
    fact(n-1);
}

int main()
{
    int n;

    scanf("%d",&n);

    fact(n);

    return 0;
}

第二种情况:n>32

这种情况下，阶乘的答案可能会非常大。甚至有可能会超出long long 的范围，这个时候我们就需要采用高精度思路来解决问题。

一般的高精度乘法代码（详情请见算法基础课高精度乘法y总代码）

#include <iostream>
#include <vector>

using namespace std;


vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}


int main()
{
    string a;
    int b;

    cin >> a >> b;

    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');

    auto C = mul(A, b);

    for (int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/39794/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。`

当然基础课中的算法可以处理一个int乘以一个超int的数，但是如果用于阶乘这种连续高精度相乘，甚至高精度乘以精度的情况,就有点复杂。但是这里是阶乘，为我们求解高精度乘以高精度提供了一种思路，就是可以把其中一个高精度的数字分解成无数int相乘。对连续的高精度乘法运算，作如下优化:
首先由于是阶乘，规模很难预测也没必要预测，建议使用vector数组。
定义一个vector数组作为乘法的被乘数，首先我们先向vector数组中存放一个数值1(毕竟1*n=n),然后遍历所有乘数(阶乘的话就是1~n)，然后把这个乘数与vector中每一位相乘，最后遍历vector,如果这个数大于10，就把这个位上的数模10，然后把进位加到下一位上。如果到了最高位还有进位的话，就把进位加入vector。最后输出的时候把vector逆序输出就好了。

图片描述如下：

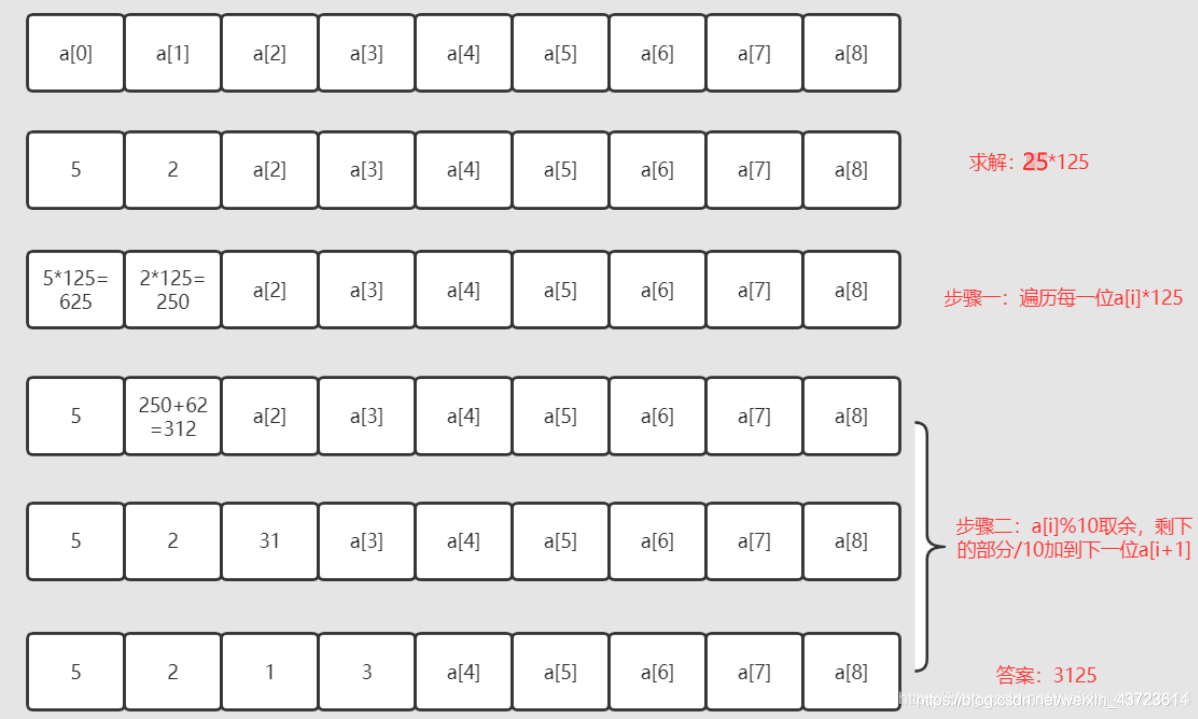
实现代码如下：

#include <iostream>
#include <vector>

using namespace std;

vector<int> res;

int main()
{
    int n;

    scanf("%d",&n);

    res.push_back(1);//把1入vector

    for(int i=2;i<=n;i++)
    {
        for(int j=0;j<res.size();j++)//把vector每一位乘上当前乘数
            res[j]*=i;
        for(int j=0;j<res.size();j++)
        {
            if(res[j]<10) continue;
            int t=res[j]/10;//当前位中的数
            res[j]%=10;
            if(j==res.size()-1)//如果是最后一位
                res.push_back(t);
            else
                res[j+1]+=t;
        }
    }

    for(int i=res.size()-1;i>=0;i--)//逆序输出即为乘积
        printf("%d",res[i]);
    return 0;
}

当然这是阶乘的情况，如果是其他高精度乘以高精度的情况，我们也可以采用这种思路，就是把其中一个高精度数作为被乘数，把另一个高精度数分解成无数个int 或者longlong范围内的数字，然后用以上思路进行求解，最后逆序输出。至于
如何分解，那就是求某个数的所有约数的问题了，至于采用什么办法这里就不赘述。