一、01背包问题
题目
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
8
代码
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int f[N][N];
int v[N], w[N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++)
{
cin >> v[i] >> w[i];
}
for(int i = 1; i <= n; i ++)
for(int j = 0; j <= m; j ++)
{
f[i][j] = f[i - 1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
01背包问题题目分析:有N个物品 背包容量为V 每个物品的的体积为vi 价值为wi 每个物品只能拿一个
目的:在不超过背包容量的情况下装的下物品的最大价值(MAX)
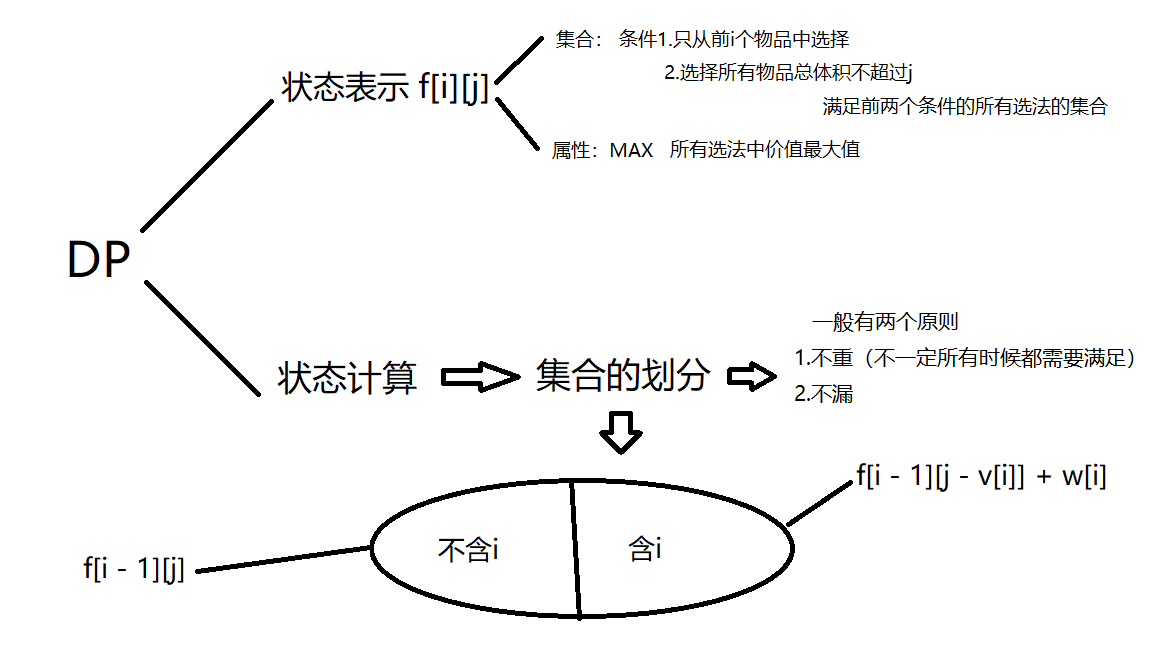
以上为y总给出基本DP问题的思考方式和01背包问题的状态计算,将所有选法分为两种一种是不选i一种是选i,不选i的最大价值显然为f[i - 1][j], 选i的最大价值为f[i - i][j - v[i] + w[i]。(这里曲线救国 直接求f[i][j]不好求先把i给减去随之背包容量也要减小v[i],求出把i给减去的最大价值再加上w[i]就是包含i的最大价值),最后我们将两者的最大值取最大值,最终我们可以得出状态转移方程为:f[i][j] = max(f[i - 1][j],f[i - 1][j - v[i] + w[i] )。
一维优化(滚动数组优化)
总结:当每次使用只会使用到自己或者只用到上一层可以使用滚动数组进行优化,将空间缩小一个维度。
如果每次使用的是上一层就从到大到小遍历 如果每次使用的是同一层就从小到大遍历
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int f[N];
int v[N], w[N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++)
{
cin >> v[i] >> w[i];
}
for(int i = 1; i <= n; i ++)
//如果每次使用的是上一层就从到大到小遍历 如果每次使用的是同一层就从小到大遍历
for(int j = m; j >= v[i]; j --)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
二、完全背包问题
题目
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
10
完全背包问题题目分析:有N个物品 背包容量为V 每个物品的的体积为vi 价值为wi 每个物品能能拿无限个
目的:在不超过背包容量的情况下装的下物品的最大价值(MAX)
完全背包问题解法和01被背包问题类似,代码和01背包问题的区别在于01背包的j从大到小遍历 完全背包问题j从小到大遍历
#include <iostream>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N];
int n, m;
int main()
{
cin >> n >> m ;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++)
for(int j = v[i]; j <= m; j ++)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}

