综合模板
#include<iostream>
using namespace std;
const int N=50;
typedef struct node *tree;
typedef int Elemtype;
struct node{
Elemtype data;
tree left;//左指针
tree right;//右指针
};
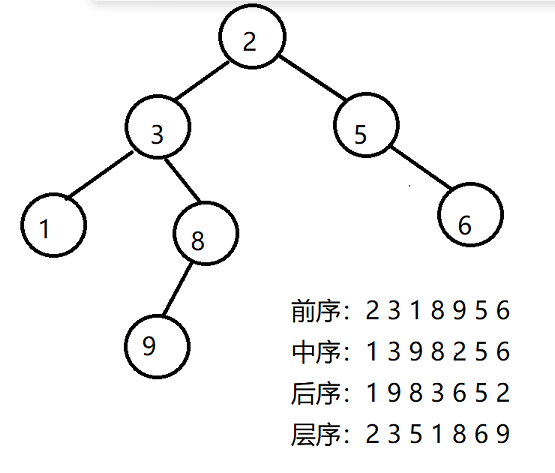
Elemtype mid[N]={1,3,9,8,2,5,6};//中序遍历序列
Elemtype pre[N]={2,3,1,8,9,5,6};//前序遍历序列
Elemtype post[N]={1,9,8,3,6,5,2};//后序遍历序列
int n;//结点数
tree build_pre_mid(int n,Elemtype pre[],Elemtype mid[])//前中序构建树
{
if(n<=0) return NULL;
Elemtype *p=mid;//指向中序序列第一个元素
while(p)//在中序遍历中找到根节点
{
if(*p==pre[0]) break;
p++;
}
//此时p指向中序中的根节点位置
int zuo=p-mid;//记录左子树的结点数
tree l=(tree)malloc(sizeof (struct node));
l->data=pre[0];
l->left=build_pre_mid(zuo,pre+1,mid);//注意左子树的根节点在pre数组中的位置是第二个,所以要加一
l->right=build_pre_mid(n-zuo-1,pre+1+zuo,mid+1+zuo);
return l;
}
tree build_post_mid(int n,Elemtype post[],Elemtype mid[])//中后序构建树
{
if(n<=0) return NULL;
Elemtype *p=mid;
while(p)
{
if(*p==post[n-1]) break;
p++;
}
int zuo=p-mid;
tree l=(tree)malloc(sizeof(struct node));
l->data=post[n-1];
l->left=build_post_mid(zuo,post,mid);
l->right=build_post_mid(n-zuo-1,post,mid+1+n);
return l;
}
void pre_print(tree l)//前序遍历(递归)
{
if(l==NULL) return ;
printf("%d ",l->data);
pre_print(l->left);
pre_print(l->right);
}
void mid_print(tree l)//中序
{
if(l==NULL) return ;
mid_print(l->left);
printf("%d ",l->data);
mid_print(l->right);
}
void post_print(tree l)//后序
{
if(l==NULL) return ;
post_print(l->left);
post_print(l->right);
printf("%d ",l->data);
}
void pre_print_2(tree l)//前序遍历(非递归)
{
if(l==NULL) return ;
tree stack[N];
int top=-1;//栈顶指针
tree p=l;
while(p||top!=-1)
{
if(p)//不断向左走
{
printf("%d ",p->data);
stack[++top]=p;
p=p->left;
}
else{//没有左孩子了,此时应该先访问该节点的右孩子,然后对其右子树重复上面的操作
p=stack[top--]->right;
}
}
}
void mid_print_2(tree l)//中序遍历
{
if(l==NULL) return ;
tree stack[N];
int top=-1;
tree p=l;
while(p||top!=-1)
{
if(p)//不断向左走,但走的同时不需要输出
{
stack[++top]=p;
p=p->left;
}
else{//没有左孩子了,应该先输出父节点
p=stack[top--];
printf("%d ",p->data);
p=p->right;
}
}
}
void post_print_2(tree l)//!!!!!难点,后序非递归
{
if(l==NULL) return ;
tree stack[N];
int top=-1;
tree p=l;
tree r=NULL;//记录刚刚访问过的结点
while(p||top!=-1)
{
if(p)
{
stack[++top]=p;
p=p->left;
}
//没有左孩子了,此时分两种情况,有右孩子时对右孩子继续上面操作
//没有右孩子时弹出该节点并输出该节点,然后继续看栈中下一个结点
else{
//此时p是空的,所有先将栈顶元素赋给p
p=stack[top];
if(p->right&&p->right!=r)
{
p=p->right;
}
else{
p=stack[top--];
printf("%d ",p->data);
r=p;
p=NULL;//置空,否则会死循环
}
}
}
}
void travel(tree l)//层序遍历,利用队列实现
{
tree queue[N];//队列
int front=-1,rear=-1;
queue[++rear]=l;
tree p;
while(front<rear)
{
p=queue[++front];
printf("%d ",p->data);
if(p->left) queue[++rear]=p->left;
if(p->right) queue[++rear]=p->right;
}
cout<<endl;
}
void reverse_travel(tree l)//从下往上,从右往左遍历二叉树
{
tree queue[N],stack[N];//先用一般层序遍历的方式入队,每次出队元素再入栈
int front=-1,rear=-1,top=-1;
queue[++rear]=l;
tree p=l;
while(front<rear)
{
p=queue[++front];
stack[++top]=p;
if(p->left) queue[++rear]=p->left;
if(p->right) queue[++rear]=p->right;
}
while(top!=-1)
{
p=stack[top--];
printf("%d ",p->data);
}
cout<<endl;
}
int height(tree l)//求树高(递归)
{
if(l==NULL) return 0;
return max(height(l->left),height(l->right))+1;
}
int height_2(tree l)//求树高非递归
{
if(l==NULL) return 0;
tree queue[N];//队列
int front=-1,rear=-1;//队头队尾指针
int last=0;//指向当前层的最后一个结点
tree p=l;
int level=0;
queue[++rear]=p;
while(front<rear)
{
p=queue[++front];
if(p->left) queue[++rear]=p->left;
if(p->right) queue[++rear]=p->right;
if(front==last){
level++;//层数加一
last=rear;
}
}
return level;
}
/*
void pre_mid_build()//前序中序构建树接口
{
for(int i=0;i<n;i++) scanf("%d",&pre[i]);
for(int i=0;i<n;i++) scanf("%d",&mid[i]);
build_pre_mid(n,pre,mid);
}
*/
int main()
{
// scanf("%d",&n);
n=7;
tree l;
l=build_pre_mid(n,pre,mid);
pre_print_2(l);
cout<<endl;
mid_print_2(l);
cout<<endl;
post_print_2(l);
cout<<endl;
printf("%d,%d\n",height(l),height_2(l));
travel(l);
reverse_travel(l);
}
重建二叉树
(根据先序和中序还原二叉树)
https://pintia.cn/problem-sets/15/problems/838
方法一:
#include<iostream>
using namespace std;
char pr[100],mi[100];
int n;
int dfs(char a[],char b[],int h)//注意形参和全局数组不要重名,这里的a和b不是原本的pr和mi,而只是其中的一段
{
if(h==0) return 0;
int i;
for(i=0;i<h;i++)
{
if(a[0]==b[i]) break;//i为左子树长度
}
int left=dfs(a+1,b,i)+1;//递归左子树,前序遍历从a+1开始
int right=dfs(a+1+i,b+i+1,h-i-1)+1;//递归右子树,前序遍历为a+1+左子树长度,中序遍历为b+左子树长度+1
//(这里加一是因为要跳过根节点)
return left>right?left:right;//返回左右深度较大的
}
int main()
{
cin>>n;
for(int i=0;i<n;i++) cin>>pr[i];
for(int i=0;i<n;i++) cin>>mi[i];
int res=dfs(pr,mi,n);
cout<<res;
}
方法二:建树
#include<iostream>
#include<malloc.h>
using namespace std;
typedef struct node *tree;
struct node{
int data;
tree left;
tree right;
};
int n;
char pr[100],mi[100];
tree build(int n,char pr[],char mi[])
{
if(n<=0) return NULL;
char *p=mi;
while(p)
{
if(*p==pr[0]) break;
p++;
}
int zuo=p-mi;//左子树长度
tree l=(tree)malloc(sizeof(struct node));
l->data=pr[0];
l->left=build(zuo,pr+1,mi);
l->right=build(n-zuo-1,pr+zuo+1,mi+zuo+1);
return l;///别忘了return
}
int height(tree l)
{
if(l==NULL) return 0;
int maxh=max(height(l->left),height(l->right));
return maxh+1;
}
int main()
{
scanf("%d%s%s",&n,pr,mi);
tree l=build(n,pr,mi);
cout<<height(l);
}
完全二叉树的层序遍历
https://pintia.cn/problem-sets/994805046380707840/problems/1336215880692482058
给定一棵完全二叉树的后序遍历,请你给出这棵树的层序遍历结果。
输入格式:
输入在第一行中给出正整数 N(≤30),即树中结点个数。第二行给出后序遍历序列,为 N 个不超过 100 的正整数。同一行中所有数字都以空格分隔。
输出格式:
在一行中输出该树的层序遍历序列。所有数字都以 1 个空格分隔,行首尾不得有多余空格。
输入样例:
8
91 71 2 34 10 15 55 18
输出样例:
18 34 55 71 2 10 15 91
#include<iostream>
using namespace std;
int a[100],n;
void tree(int x)
{
if(x>n) return;
//按照题目所给的遍历方式递归,后序时就先递归左子树即x*2,然后右子树x*2+1,最后输入根节点
tree(x*2);
tree(x*2+1);
cin>>a[x];
}
int main()
{
scanf("%d",&n);
tree(1);//从根节点开始
for(int i=1;i<=n;i++)
{
if(i>1) printf(" ");
printf("%d",a[i]);
}
}
L2-006 树的遍历 (25 分)
https://pintia.cn/problem-sets/994805046380707840/problems/994805069361299456
给定一棵二叉树的后序遍历和中序遍历,请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。
输入格式:
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。
输出格式:
在一行中输出该树的层序遍历的序列。数字间以1个空格分隔,行首尾不得有多余空格。
输入样例:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
输出样例:
4 1 6 3 5 7 2
#include<iostream>
#include<malloc.h>
using namespace std;
int n;
int post[100], mid[100];//post为后序遍历,mid为中序遍历
typedef struct node *tree;
struct node{
int data;
tree left;
tree right;
};
tree build(int n,int post[],int mid[])//建树
{
if(n<=0) return NULL;
//先找到根节点在中序遍历中的位置,就能确定左子树和右子树范围
//每次递归时,post[]数组的最后一个为根节点
int *p=mid;
int i;
while(p)
{
if(*p==post[n-1]) break;
p++;
}
int left=p-mid;//左子树长度
tree l=(tree)malloc(sizeof(struct node));
l->data=post[n-1];
l->left=build(left,post,mid);
l->right=build(n-left-1,post+left,mid+left+1);
return l;
}
void travel(tree l)//层序遍历
{
tree q[100];
int front = 0,rear = 0;
int count=0;
q[0] = l;//入队
while(rear>=front){
tree t = q[front++];
if(count==0){
printf("%d",t->data);
count++;
}else{
printf(" %d",t->data);
}
if(t->left){
q[++rear] = t->left;
}
if(t->right){
q[++rear] = t->right;
}
}
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&post[i]);
for(int i=0;i<n;i++) scanf("%d",&mid[i]);
tree l;
l=build(n,post,mid);
travel(l);
}
用非递归的形式分别实现前、中、后序遍历
void preorder(tree l)//非递归先序
{
tree stack[N];
int top=-1;
if(l==NULL) return ;
tree p=l;
while(p||top!=-1)
{
if(p)
{
printf("%d ",p->data);//访问完仍需入栈,以为后续要访问其右节点
stack[++top]=p;
p=p->left;
}
else{
p=stack[top--]->right;
}
}
}
void midorder(tree l)//非递归的中序
{
tree stack[N];
int top=-1;//栈顶指针
if(l==NULL) return ;
// stack[++top]=l;
tree p=l;
while(p||top!=-1)
{
if(p)//一路向左
{
stack[++top]=p;
p=p->left;
}
else{//没有左孩子了,访问栈顶元素,并将其右孩子入栈
printf("%d ",stack[top]->data);
p=stack[top--]->right;
}
}
}
void postorder(tree l)//非递归后序
{
if(l==NULL) return ;
tree stack[N];
int top=-1;
tree p=l;
tree r=NULL;//记录刚刚访问过的结点
while(p||top!=-1)
{
if(p)
{
stack[++top]=p;
p=p->left;
}
//没有左孩子了,此时分两种情况,有右孩子时对右孩子继续上面操作
//没有右孩子时弹出该节点并输出该节点,然后继续看栈中下一个结点
else{
//此时p是空的,所有先将栈顶元素赋给p
p=stack[top];
if(p->right&&p->right!=r)
{
p=p->right;
}
else{
p=stack[top--];
printf("%d ",p->data);
r=p;
p=NULL;//置空,否则会死循环
}
}
}
}
L2-011 玩转二叉树 (25 分)
https://pintia.cn/problem-sets/994805046380707840/problems/994805065406070784
给定一棵二叉树的中序遍历和前序遍历,请你先将树做个镜面反转,再输出反转后的层序遍历的序列。所谓镜面反转,是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。
输入格式:
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。
输出格式:
在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分隔,行首尾不得有多余空格。
输入样例:
7
1 2 3 4 5 6 7
4 1 3 2 6 5 7
输出样例:
4 6 1 7 5 3 2
层序遍历中左右顺序交换即可
#include<iostream>
#include<malloc.h>
using namespace std;
int n;
int pr[100], mid[100];//post为后序遍历,mid为中序遍历
typedef struct node *tree;
struct node{
int data;
tree left;
tree right;
};
tree build(int n,int pr[],int mid[])//建树
{
if(n<=0) return NULL;
//先找到根节点在中序遍历中的位置,就能确定左子树和右子树范围
//每次递归时,post[]数组的最后一个为根节点
int *p=mid;
int i;
while(p)
{
if(*p==pr[0]) break;
p++;
}
int left=p-mid;//左子树长度
tree l=(tree)malloc(sizeof(struct node));
l->data=pr[0];
l->left=build(left,pr+1,mid);
l->right=build(n-left-1,pr+left+1,mid+left+1);
return l;
}
void travel(tree l)//层序遍历
{
tree q[100];
int front = 0,rear = 0;
int count=0;
q[0] = l;//入队
while(rear>=front){
tree t = q[front++];
if(count==0){
printf("%d",t->data);
count++;
}else{
printf(" %d",t->data);
}
if(t->right){
q[++rear] = t->right;
}
if(t->left){
q[++rear] = t->left;
}
}
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&mid[i]);
for(int i=0;i<n;i++) scanf("%d",&pr[i]);
tree l;
l=build(n,pr,mid);
travel(l);
}
3540. 二叉搜索树
https://www.acwing.com/problem/content/description/3543/
输入一系列整数,利用所给数据建立一个二叉搜索树,并输出其前序、中序和后序遍历序列。
输入格式
第一行一个整数 n,表示输入整数数量。
第二行包含 n 个整数。
输出格式
共三行,第一行输出前序遍历序列,第二行输出中序遍历序列,第三行输出后续遍历序列。
输入中可能有重复元素,但是输出的二叉树遍历序列中重复元素不用输出。
数据范围
1≤n≤100,
输入元素取值范围 [1,1000]。
输入样例:
5
1 6 5 9 8
输出样例:
1 6 5 9 8
1 5 6 8 9
5 8 9 6 1
#include<iostream>
#include<malloc.h>
#include<algorithm>
#include<queue>
using namespace std;
typedef struct node *tree;
struct node{
int data;
tree left;
tree right;
};
int n;
int a[100];
tree root=NULL;//若不用全局变量,采用传参的方式主要以引用的方式
void insert(int k)
{
if(root==NULL)
{
root=(tree)malloc(sizeof(struct node));
root->data=k;
return;
}
tree current=root;
tree parent=NULL;
while(true)
{
parent=current;
if(k<parent->data)
{
current=parent->left;
if(current==NULL)
{
parent->left=(tree)malloc(sizeof(struct node));////!!!一定注意这里要用parent指针而不是current
parent->left->data=k;
return;
}
}
else if(k>parent->data)
{
current=parent->right;
if(current==NULL)
{
parent->right=(tree)malloc(sizeof (struct node));
parent->right->data=k;
return ;
}
}
else return;
}
}
/*
void layershow(tree root)
{
queue<tree> que;
if(root)
{
cout<<root->data;
que.push(root);
}
while(!que.empty())
{
tree root=que.front();
que.pop();
if(root->left)
{
cout<<" "<<root->left->data;
que.push(root->left);
}
if(root->right)
{
cout<<" "<<root->right->data;
que.push(root->right);
}
}
}
*/
void preorder(tree root)
{
if (!root) return;
printf("%d ",root->data);
preorder(root->left);
preorder(root->right);
}
void inorder(tree root)
{
if (!root) return;
inorder(root->left);
printf("%d ",root->data);
inorder(root->right);
}
void postorder(tree root)
{
if (!root) return;
postorder(root->left);
postorder(root->right);
printf("%d ",root->data);
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&a[i]);
insert(a[i]);
}
preorder(root);
cout<<endl;
inorder(root);
cout<<endl;
postorder(root);
}
L3-010 是否完全二叉搜索树 (30 分)
https://pintia.cn/problem-sets/994805046380707840/problems/994805049870368768
将一系列给定数字顺序插入一个初始为空的二叉搜索树(定义为左子树键值大,右子树键值小),你需要判断最后的树是否一棵完全二叉树,并且给出其层序遍历的结果。
输入格式:
输入第一行给出一个不超过20的正整数N;第二行给出N个互不相同的正整数,其间以空格分隔。
输出格式:
将输入的N个正整数顺序插入一个初始为空的二叉搜索树。在第一行中输出结果树的层序遍历结果,数字间以1个空格分隔,行的首尾不得有多余空格。第二行输出YES,如果该树是完全二叉树;否则输出NO。
输入样例1:
9
38 45 42 24 58 30 67 12 51
输出样例1:
38 45 24 58 42 30 12 67 51
YES
输入样例2:
8
38 24 12 45 58 67 42 51
输出样例2:
38 45 24 58 42 12 67 51
NO
完全二叉树的定义是:深度为n的二叉树,其全部深度n-1的节点为满,而深度为n的节点只能聚集在左侧。那么我们可以层次遍历找到第一个NULL节点,记录遍历的节点个数,如果其个数为n的话说明为完全二叉树,否则不是。
#include<iostream>
#include<malloc.h>
#include<algorithm>
#include<queue>
using namespace std;
typedef struct node *tree;
struct node{
int data;
tree left;
tree right;
};
int n;
int a[100];
tree root=NULL;
void insert(int k)
{
if(root==NULL)
{
root=(tree)malloc(sizeof(struct node));
root->data=k;
return;
}
tree current=root;
tree parent=NULL;
while(true)
{
parent=current;
if(k>parent->data)
{
current=parent->left;
if(current==NULL)
{
parent->left=(tree)malloc(sizeof(struct node));
parent->left->data=k;
return;
}
}
else if(k<parent->data)
{
current=parent->right;
if(current==NULL)
{
parent->right=(tree)malloc(sizeof (struct node));
parent->right->data=k;
return ;
}
}
else return;
}
}
void layershow(tree root)
{
queue<tree> que;
if(root)
{
cout<<root->data;
que.push(root);
}
while(!que.empty())
{
tree root=que.front();
que.pop();
if(root->left)
{
cout<<" "<<root->left->data;
que.push(root->left);
}
if(root->right)
{
cout<<" "<<root->right->data;
que.push(root->right);
}
}
}
void check(tree root)
{
tree q[100];
int hh=0,tt=0;
q[0]=root;
int num=0;
while(hh<=tt)
{
tree t=q[hh++];
if(!t) break;
q[++tt]=t->left;
q[++tt]=t->right;
num++;
}
if(num==n)
printf("YES");
else printf("NO");
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&a[i]);
insert(a[i]);
}
layershow(root);
cout<<endl;
check(root);
}
www.acwing.com/problem/content/description/1552/
对于完全二叉树的插入方式就是
void tree(int x)
{
if(x>n) return;
//按照题目所给的遍历方式递归,后序时就先递归左子树即x*2,然后右子树x*2+1,最后输入根节点
tree(x*2);
tree(x*2+1);
cin>>a[x];
}
因此此题只要知道一种输入方式即可,而二叉排序树的中序是确定的即按从小到大排序
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010;
int a[N],b[N];
int cnt=0,n;
void insert(int x)
{
if(x>n) return;
insert(x*2);
b[x]=a[cnt++];
insert(x*2+1);
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
sort(a,a+n);
insert(1);
for(int i=1;i<=n;i++) printf("%d ",b[i]);
}
树的左视图和右视图
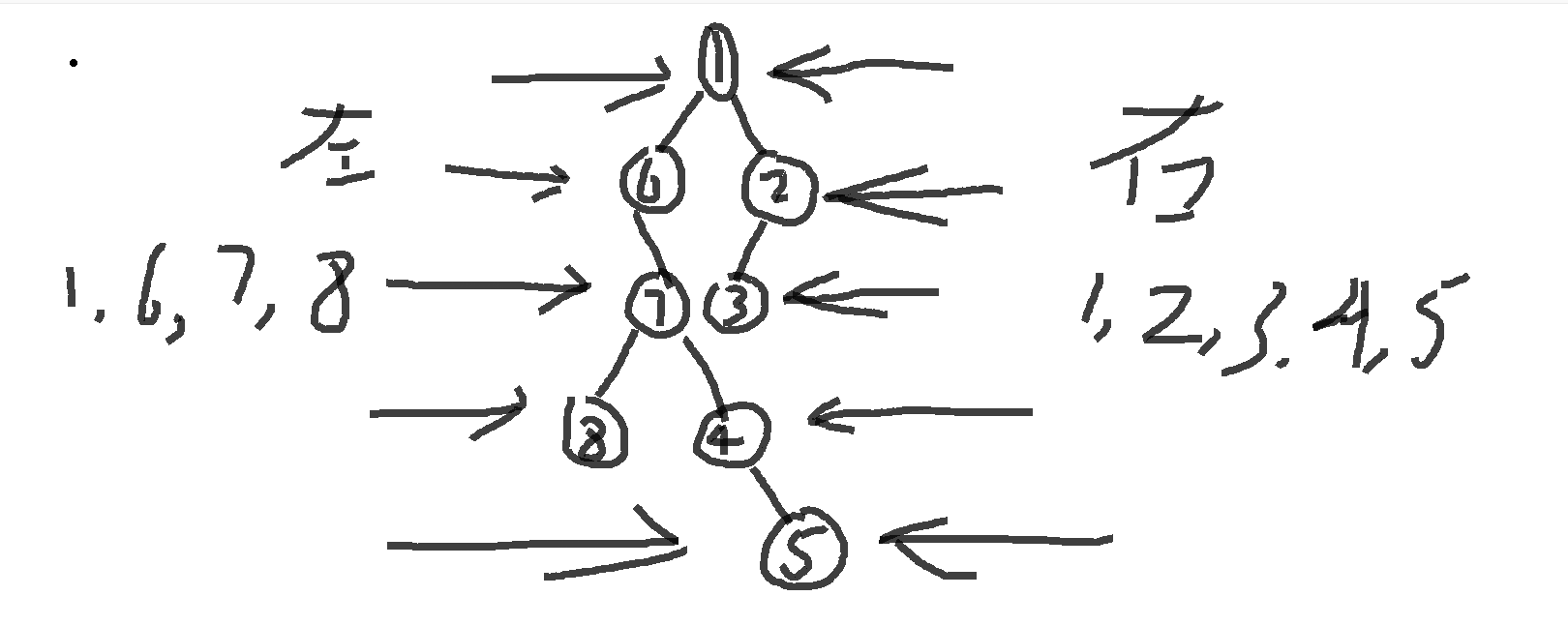
上面左视图还有一个5,忘了画
左视图:从左往右看,只能看到每一层的最左边的结点,即左视图为从上到下依次输出每层的最左边的结点。
右视图:同理。
例题
(没有题目链接)
浪漫侧影
我们将二叉树的“侧影”定义为从一侧能看到的所有结点从上到下形成的序列。例如下图这棵二叉树,其右视图就是 { 1, 2, 3, 4, 5 },左视图就是 { 1, 6, 7, 8, 5 }。
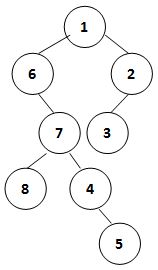
于是让我们首先通过一棵二叉树的中序遍历序列和后序遍历序列构建出一棵树,然后你要输出这棵树的左视图和右视图。
输入格式:
输入第一行给出一个正整数 N (≤20),为树中的结点个数。随后在两行中先后给出树的中序遍历和后序遍历序列。树中所有键值都不相同,其数值大小无关紧要,都不超过 int 的范围。
输出格式:
第一行输出右视图,第二行输出左视图,格式如样例所示。
输入样例:
8
6 8 7 4 5 1 3 2
8 5 4 7 6 3 2 1
输出样例:
R: 1 2 3 4 5
L: 1 6 7 8 5
思路,根据中序和后序构建二叉树,然后记录左视图和右视图的基础是层序遍历,遍历每一层的时候记录当前层的第一个结点(最左)即左视图,记录最后一个结点即右视图
代码:(只是输出左右视图,格式和题目要求不一致)
#include<iostream>
using namespace std;
typedef struct node *tree;
struct node{
int data;
tree left;
tree right;
};
int n;
int post[110],mid[110];
tree build(int h,int post[],int mid[])
{
if(h<=0) return NULL;
int *p=mid;
int i;
while(p)
{
if(*p==post[h-1]) break;
p++;
}
int zuo=p-mid;//左子树长度
tree l=(tree)malloc(sizeof(struct node));
l->data=post[h-1];
l->left=build(zuo,post,mid);
l->right=build(h-zuo-1,post+zuo,mid+zuo+1);
return l;
}
void travel(tree l)
{
int count=0;
if(l==NULL) return ;
tree q[110];
int hh=0,tt=0;
q[0]=l;
int res1[110];//记录左视图
int res2[110];//记录右视图
int lo1=0,lo2=0;
while(hh<=tt)
{
int len=tt-hh+1;
cout<<len<<endl;//每一层的节点数
for(int i=0;i<len;i++)//每一层
{
tree t=q[hh++];
if(t->left) q[++tt]=t->left;
if(t->right) q[++tt]=t->right;
if(i==0)
{
res1[lo1++]=t->data;
}
if(i==len-1)
{
res2[lo2++]=t->data;
}
}
}
printf("L:");
for(int i=0;i<lo1;i++) printf("%d ",res1[i]);
cout<<endl;
printf("R:");
for(int i=0;i<lo1;i++) printf("%d ",res2[i]);
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&post[i]);
for(int i=0;i<n;i++) scanf("%d",&mid[i]);
tree l;
l=build(n,post,mid);
travel(l);
}
7-6 笛卡尔树 (25 分)
https://pintia.cn/problem-sets/15/problems/858
笛卡尔树是一种特殊的二叉树,其结点包含两个关键字K1和K2。首先笛卡尔树是关于K1的二叉搜索树,即结点左子树的所有K1值都比该结点的K1值小,右子树则大。其次所有结点的K2关键字满足优先队列(不妨设为最小堆)的顺序要求,即该结点的K2值比其子树中所有结点的K2值小。给定一棵二叉树,请判断该树是否笛卡尔树。
输入格式:
输入首先给出正整数N(≤1000),为树中结点的个数。随后N行,每行给出一个结点的信息,包括:结点的K1值、K2值、左孩子结点编号、右孩子结点编号。设结点从0~(N-1)顺序编号。若某结点不存在孩子结点,则该位置给出−1。
输出格式:
输出YES如果该树是一棵笛卡尔树;否则输出NO。
输入样例1:
6
8 27 5 1
9 40 -1 -1
10 20 0 3
12 21 -1 4
15 22 -1 -1
5 35 -1 -1
输出样例1:
YES
输入样例2:
6
8 27 5 1
9 40 -1 -1
10 20 0 3
12 11 -1 4
15 22 -1 -1
50 35 -1 -1
输出样例2:
NO
思路:
先构建树,找到根节点,然后采用层序遍历的方式,先将根节点入队,依次判断左右结点是否满足要求,满足就再入队,循环。
先上错误代码:
该段代码采用的是层序遍历的思路
#include<iostream>
using namespace std;
const int N=1010;
bool h_f[N];
struct node{
int r1,r2;
int left,right;
}tree[N];
int n;
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++)
{
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
h_f[c]=true;
h_f[d]=true;
tree[i]={a,b,c,d};
}
int root=0;
while(h_f[root]) root++;
int hh=0,tt=0;
int q[N];
q[0]=root;
bool flag=true;
while(hh<=tt)
{
int t=q[hh++];
if(tree[t].left!=-1)
{
if(tree[tree[t].left].r1>=tree[t].r1||tree[tree[t].left].r2<tree[t].r2)
{
flag=false;
break;
}
q[++tt]=tree[t].left;
}
if(tree[t].right!=-1)
{
if(tree[tree[t].right].r1<=tree[t].r1||tree[tree[t].right].r2<tree[t].r2)
{
flag=false;
break;
}
q[++tt]=tree[t].right;
}
}
if(!flag) printf("NO");
else printf("YES");
}
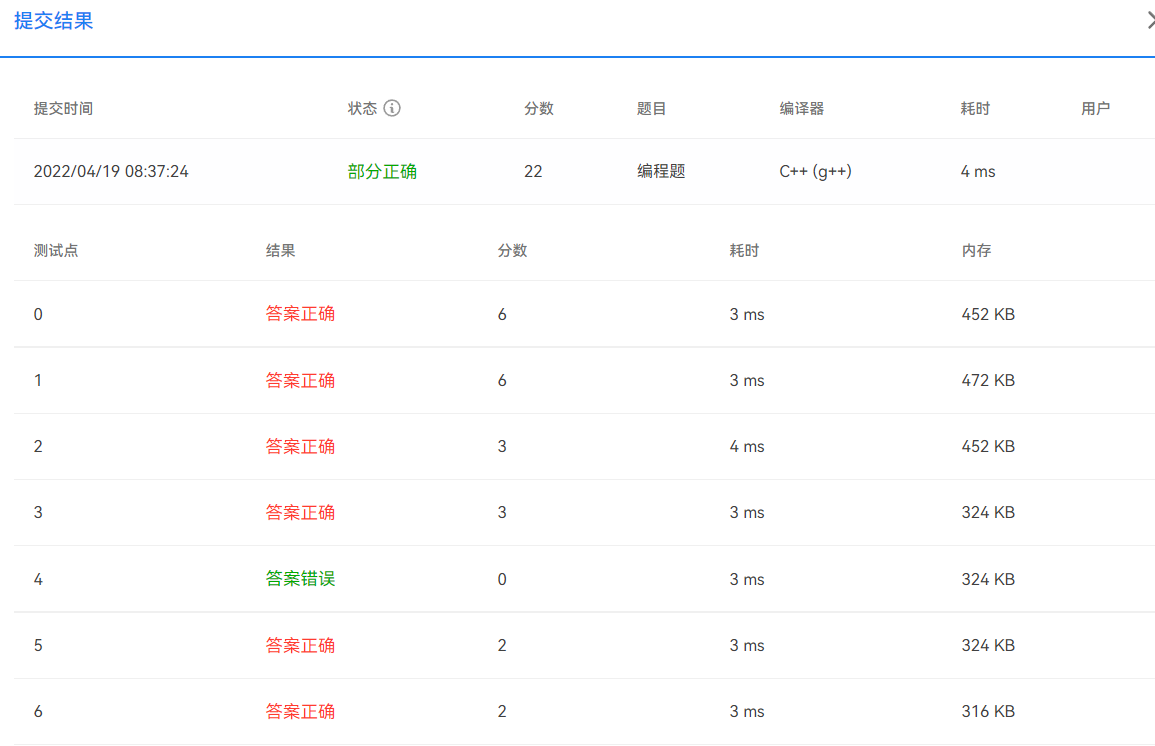
查了一下别人的代码,发现我忽略了二叉搜索树的一个条件,构成二叉搜索树的两个条件:
1.左节点的值严格小于根节点,右节点严格大于根节点(除非题目说了可以相等)
2.所有左子树的值要小于根节点,所有右子树上的值要大于根节点
也就是说,采用上面的层序遍历的思路,可能会存在左子树中某个结点,该节点的右儿子结点大于该节点的值,且右儿子结点大于根节点的值(最上面的结点)。
因此采用递归的方式,限制左右子树的结点最小最大值。
先构建树,找到根节点,然后递归判断左子树的两个键值和根节点相比是否符合大小关系,再递归右子树。
#include<iostream>
using namespace std;
const int N=1010;
struct node{
int r1,r2;
int left,right;
}tree[N];
bool h_f[1010];//判断是否有父节点
int n;
bool dfs(int u,int maxm,int minm)
{
if(u==-1) return true;
int r1=tree[u].r1;
int r2=tree[u].r2;
if(r1>=maxm||r1<=minm) return false;//不符合构成二叉搜索树
int left=tree[u].left;
int right=tree[u].right;
if(left!=-1&&(tree[left].r1>r1||tree[left].r2<r2)) return false;
if(right!=-1&&(tree[right].r1<r1||tree[right].r2<r2)) return false;
return dfs(left,r1,minm)&&dfs(right,maxm,r1);
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++)
{
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
tree[i]={a,b,c,d};
//c和d是子节点
h_f[c]=true;
h_f[d]=true;
}
int root=0;//找根节点
while(h_f[root]) root++;
bool res;
res=dfs(root,0x3f3f3f3f,-0x3f3f3f3f);
if(res) printf("YES");
else printf("NO");
}
AVL树
https://www.acwing.com/problem/content/description/1554/
#include<iostream>
#include<algorithm>
using namespace std;
const int N=40;
int l[N],r[N],v[N];
int n;
int h[N];
int idex;
void updata(int u)
{
h[u]=max(h[l[u]],h[r[u]])+1;
}
void L(int &u)//左旋
{
int p=r[u];//右儿子作为新根
r[u]=l[p];
l[p]=u;//原来的根作为新根的左儿子
updata(u);
updata(p);
u=p;
}
void R(int &u)//右旋
{
int p=l[u];
l[u]=r[p];
r[p]=u;
updata(u);
updata(p);
u=p;
}
int get_balance(int u)
{
return h[l[u]]-h[r[u]];
}
void insert(int &u,int w)
{
if(u==0){
u =++idex;
v[u] =w;
}
else if(w<v[u]){//插到左子树上
insert(l[u],w);
//左子树比右子树高2
if(get_balance(u) ==2){
//以左子树为根,其左子树比右子树高1(极左情况,右旋u)
if(get_balance(l[u])==1) R(u);
else L(l[u]),R(u);
}
}
else{
insert(r[u],w);
if(get_balance(u)==-2)
{
if(get_balance(r[u])==-1) L(u);
else R(r[u]),L(u);
}
}
updata(u);
}
int main()
{
scanf("%d",&n);
int root=0;
for(int i=0;i<n;i++)
{
int w;
scanf("%d",&w);
insert(root,w);
}
cout<<v[root];
}

