数据结构特点

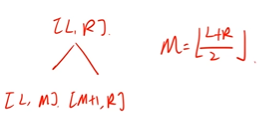
为什么叫线段树？
因为它是把原序列以及其子序列（一个个线段）组织成一棵树的形式。树的根节点为原序列，子节点依次对半分序列，直到叶节点，叶节点是单个数，也没办法再往下分了。

而对于每个结点而言，它存储了三个属性：

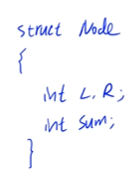
+ 结点所表示区间（线段）的左端点$L$
+ 结点所表示区间（线段）的右端点$R$
+ 结点所表示区间（线段）的和$sum$

样例：1-7的序列组织成线段树

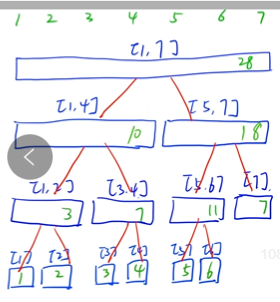
我们发现，原本的区间，在最底层其实是一个个元素构成的叶节点。
我们可以发现，从根节点向下递归地过程中，节点的长度逐渐缩小，类似一个不断二分的过程，最后确定为一个点。

整棵线段树中，所有节点的个数是小于$4n$的（$n$是区间、线段的长度、也即叶节点个数）

实际存储的数据结构

整体上类似于堆的存储结构：下标从1开始的一维数组
父节点：x>>1
左儿子：x<<1
右儿子：x<<1|1

而这里因为每个结点要存储三个属性，所以这里的一维数组，实际是一维结构体数组。

应用与功能

树状数组的初始化

void pushup(int u)  //计算节点u的和
{      //父节点的和等于两个儿子的和
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void build(int u, int l, int r)
{  //u节点编号，l左边界，r右边界
    if (l == r) tr[u] = {l, r, w[r]};  //如果递归到了最底层叶节点，那其自身的属性是确定的
    else
    {
        tr[u] = {l, r};  //如果还没到叶节点，其左右边界是确定的
        int mid = l + r >> 1;  //二分区间，往下继续递归
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);  //向下递归建立
        pushup(u); //递归完了回溯计算父节点
    }
}

主函数里：build(1, 1, n);

单点修改

我们只修改信息需要变化的节点，这是一个递归+回溯的过程。

void modify(int u, int x, int v)
{  //u为编号，给数x加上v
    if (tr[u].l == tr[u].r) tr[u].sum += v; //递归边界，如果找到这个点了
    else
    { //没有找到这个点 二分区间，向下递归
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);  //判断是在左儿子还是右儿子
        else modify(u << 1 | 1, x, v);
        pushup(u);  //递归好了要回溯重新计算当前节点的sum，因为在修改的过程中变化了
    }
}

区间查询

从根节点不断递归向下，直到完全包含为止

int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;  //当前节点的左右边界被查询区间完全包含了，不继续向下递归，返回sum
    int mid = tr[u].l + tr[u].r >> 1; //继续向下递归
    int sum = 0;   //如果和左孩子或者右孩子有交集，则继续向下递归
    if (l <= mid) sum += query(u << 1, l, r);
    if (r > mid) sum += query(u << 1 | 1, l, r);
    return sum;  
}

代码举例：AcWing 1264. 动态求连续区间和

裸题就不多分析啦，直接上代码

#include<iostream>
using namespace std;
const int N=100010;
int n,m,w[N];
int k,a,b;
struct Node
{
    int l,r,sum;
}tri[4*N];

void pushup(int u)
{
    tri[u].sum=tri[u<<1].sum+tri[u<<1|1].sum;
}
void build(int u,int l,int r)
{
    if(l==r) tri[u]={l,r,w[r]}; //注意这里是w[r]或者w[l],这里绝不是w[u]
    else                        //w是存元素值的
    {                           //tri的节点标号是树节点的标号，与其无关
        tri[u]={l,r};           //但是我们直到l，r是可以对应到w上的一段区间的！
        int mid=l+r>>1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
        pushup(u);
    }
}
int query(int u,int l,int r)
{
    if(l<=tri[u].l&&r>=tri[u].r) return tri[u].sum;
    int mid=tri[u].l+tri[u].r>>1;
    int sum=0;
    if(l<=mid) sum+=query(u<<1,l,r);  //在递归的过程中，后两个参数是完全不变的，只是不断往下递归，因为要求的是一个区间的值，区间的左右界怎么能变呢？
    if(r>mid) sum+=query(u<<1|1,l,r);  
    return sum;
}
void modify(int u,int x,int v)
{
    if(tri[u].l==tri[u].r) tri[u].sum+=v;
    else
    {
        int mid=tri[u].l+tri[u].r>>1;
        if(x<=mid) modify(u<<1,x,v);
        else    modify(u<<1|1,x,v);
        pushup(u);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&w[i]);
    build(1,1,n);

    while(m--)
    {
        scanf("%d%d%d",&k,&a,&b);
        if(k==0) printf("%d\n",query(1,a,b));
        else    modify(1,a,b);
    }
    return 0;
}