3.搜索与图论
DFS
1.全排列
#include<bits/stdc++.h>
using namespace std;
const int N=10;
vector<int> a;
bool st[N];
int n;
void dfs(int x,int num){
if(num>n){
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
cout<<endl;
return;
}
for(int i=1;i<=n;i++){
if(!st[i]){
a.push_back(i);
st[i]=true;
dfs(i,num+1);
st[i]=false;
a.pop_back();
}
}
}
int main(){
cin>>n;
dfs(1,1);
return 0;
}
2.n皇后问题
#include<bits/stdc++.h>
using namespace std;
const int N=25;
int n;
char g[N][N];
bool col[N],dg[N],udg[N];
void dfs(int num){
if(num>n){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cout<<g[i][j];
}
cout<<endl;
}
cout<<endl;
return;
}else{
for(int i=1;i<=n;i++){
if(!col[i]&&!dg[i+num-1]&&!udg[n-i+num]){
col[i]=dg[i+num-1]=udg[n-i+num]=1;
g[num][i]='Q';
dfs(num+1);
g[num][i]='.';
col[i]=dg[i+num-1]=udg[n-i+num]=0;
}
}
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
g[i][j]='.';
}
}
dfs(1);
return 0;
}
BFS
1.走迷宫
#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n,m;
int g[N][N];
int res[N][N];
int xx[4]={0,0,1,-1};
int yy[4]={1,-1,0,0};
int bfs(){
queue<int> qx,qy;
qx.push(1);qy.push(1);
memset(res,-1,sizeof res);
res[1][1]=0;
while(!qx.empty()){
int x=qx.front();qx.pop();
int y=qy.front();qy.pop();
for(int i=0;i<4;i++){
int dx=xx[i]+x;
int dy=yy[i]+y;
if(g[dx][dy]==0&&res[dx][dy]==-1&&dx<=n&&dx>=1&&dy>=1&&dy<=m){
res[dx][dy]=res[x][y]+1;
if(dx==n&&dy==m)return res[dx][dy];
qx.push(dx);qy.push(dy);
}
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%d",&g[i][j]);
}
}
cout<<bfs();
return 0;
}
2.八数码


#include<bits/stdc++.h>
using namespace std;
const string End="12345678x";//定义目标状态
//转移方式
int xx[4]={0,0,1,-1};
int yy[4]={1,-1,0,0};
int bfs(string s){
queue<string> q;//存储状态
unordered_map<string,int> d;//存储每个状态对应的次数
q.push(s);
d[s]=0;
while(q.size()){
string str=q.front();q.pop();
int distance=d[str];
if(str==End)return distance;
//查询x在字符串中的下标,然后转换为在矩阵中的坐标
int k=str.find('x');
int x=k/3,y=k%3;
for(int i=0;i<4;i++){
//求转移后x的坐标
int dx=x+xx[i],dy=y+yy[i];
//当前坐标没有越界
if(dx>=0&&dx<3&&dy>=0&&dy<3){
//转移x
swap(str[k],str[dx*3+dy]);
//如果当前状态是第一次遍历,记录距离,入队
if(!d.count(str)){
d[str]=distance+1;
q.push(str);
}
//还原状态
swap(str[k],str[dx*3+dy]);
}
}
}
return -1;//无法转换到目标状态,即不存在解决方案,
}
int main(){
string start;
for(int i=0;i<9;i++){
char c;
cin>>c;
start+=c;
}
cout<<bfs(start);
return 0;
}
树与图的深度优先遍历
//邻接表
int h[N], e[N * 2], ne[N * 2], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u){//dfs 框架
st[u]=true; // 标记一下,记录为已经被搜索过了,下面进行搜索过程
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(!st[j]) {
dfs(j);
}
}
}
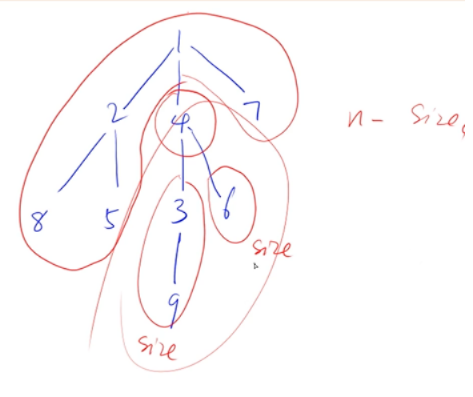
1.树的重心 (求最小的最大连通块)
using namespace std;
const int N=1e5+10;
int h[N],e[2*N],ne[2*N],idx;
bool st[N];
int n;
int ans=N;//答案 存储最大连通块的最小值
void add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx;
idx++;
}
//返回以u为根的子树中节点的个数,包括u节点
int dfs(int u){
st[u]=true;
int res=0;//存储最大连通块的值
int sum=1;//以u为根的结点数 n-sum可以算其之上的连通块所有结点数
//访问每个子节点
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(st[j]==false){
int s=dfs(j);
sum+=s;
res=max(res,s);
}
}
//cout<<res<<" ";
res=max(res,n-sum);
//cout<<res<<"MAXRES"<<endl;
ans=min(res,ans);
return sum;
}
int main(){
memset(h,-1,sizeof h);
cin>>n;
for(int i=0;i<n-1;i++){
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
dfs(1);//可以任意选定一个节点开始 u<=n
cout<<ans<<endl;
return 0;
}
树与图的广度优先遍历
1.图中点的层次
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int head[N],e[N],ne[N],idx;
int d[N];
int q[N];
int n,m;
void add(int a,int b){
e[idx]=b;
ne[idx]=head[a];
head[a]=idx;
idx++;
}
int bfs(int u){
queue<int> q;
q.push(u);
memset(d,-1,sizeof d);
d[1]=0;
while(q.size()){
int t=q.front();q.pop();
for(int i=head[t];i!=-1;i=ne[i]){
int j=e[i];
if(d[j]==-1){//如果j没有被遍历过
d[j]=d[t]+1;//d[j]存储j节点离起点的距离,同时标记为访问过
q.push(j);//把j结点 压入队列
}
}
}
return d[n];
}
int main(){
cin>>n>>m;
memset(head,-1,sizeof head);
for(int i=1;i<=m;i++){
int a,b;
cin>>a>>b;
add(a,b);
}
cout<<bfs(1);
return 0;
}
拓扑排序
1.有向图的拓扑序列(判断是否为有向无环图)
拓扑排序只适用于AOV网 (有向无环图)
算法流程:
用队列来执行 ,初始化讲所有入度为0的顶点入队。
主要由以下两步循环执行,直到不存在入度为 0 的顶点为止
- 选择一个入度为 0 的顶点,并将它输出;
- 删除图中从顶点连出的所有边。
循环结束后,
若输出的顶点数小于图中的顶点数,则表示该图存在回路,即无法拓扑排序,
否则,输出的就是拓扑序列 (不唯一)
加深理解:
一开始有点不理解,为了加深理解手动模拟了一下,发现确实如此:
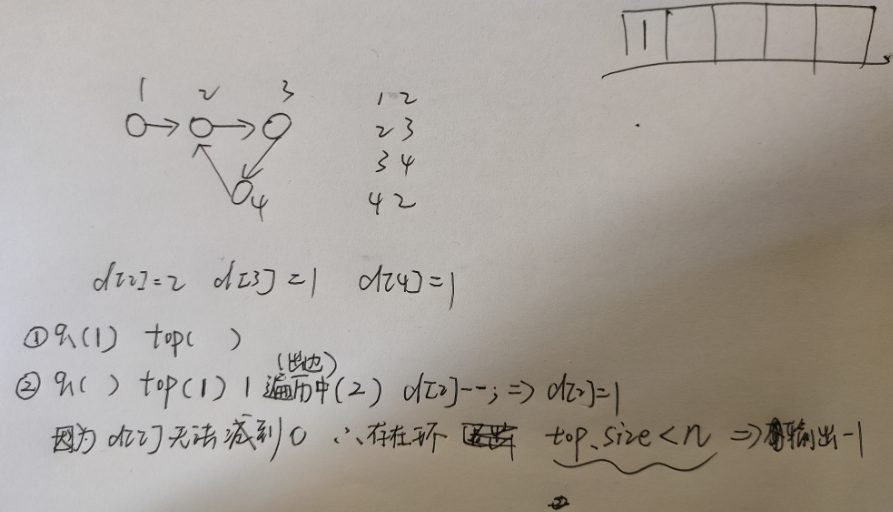
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m;
int h[N],e[N],ne[N],idx;
vector<int> top;//top是拓扑排序的序列,
int d[N];//点的入度!
void add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx;
idx++;
}
bool topsort(){
queue<int> q;
for(int i=1;i<=n;i++){
if(d[i]==0)q.push(i);
}
while(q.size()){
int t=q.front();
q.pop();
top.push_back(t);//加入到拓扑序列中
for(int i=h[t];i!=-1;i=ne[i]){
//遍历t的出边
int j=e[i];
d[j]--;
if(d[j]==0)q.push(j);//如果j入度为0,加入队列当中
}
}
if(top.size()<n)return false;
else return true;
}
int main(){
cin>>n>>m;
memset(h,-1,sizeof h);
for(int i=0;i<m;i++){
int a,b;
cin>>a>>b;
add(a,b);
d[b]++;// a -> b , b的入度++
}
if(topsort()){
for(int i=0;i<top.size();i++)cout<<top[i]<<" ";
}else{
cout<<-1;
}
return 0;
}
最短路问题
总结
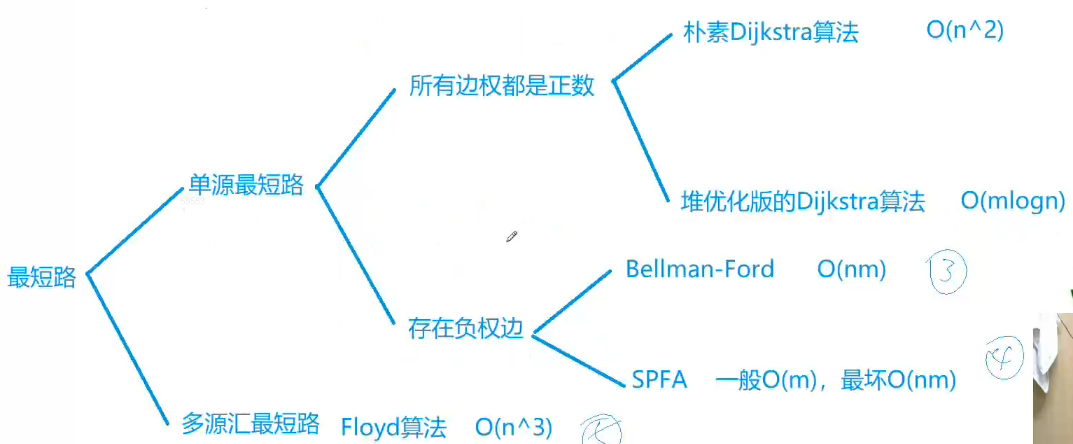

Dijkstra
1.Dijkstra求最短路 I(朴素版本)
#include<bits/stdc++.h>
using namespace std;
const int N=510;
int d[N][N];
int dist[N];
bool st[N];
int n,m;
int dijkstra(){
memset(dist,0x3f,sizeof dist);
dist[1]=0;
for(int i=1;i<=n;i++){//n次遍历
int t=-1;
for(int j=1;j<=n;j++){//找到最小的那个
if(!st[j]&&(t==-1||dist[j]<dist[t]))
t=j;
}
st[t]=true;
for(int j=1;j<=n;j++){
//更新
if(dist[t]+d[t][j]<dist[j]){
dist[j]=dist[t]+d[t][j];
}
}
}
if(dist[n]!=0x3f3f3f3f)
return dist[n];
else return -1;
}
int main(){
memset(d,0x3f,sizeof d);
cin>>n>>m;
for(int i=1;i<=m;i++){
int a,b,c;
cin>>a>>b>>c;
d[a][b]=min(d[a][b],c);
}
cout<<dijkstra()<<endl;
return 0;
}
2.Dijkstra求最短路II (堆优化版本)
#include<bits/stdc++.h>
using namespace std;
const int N=150000;
typedef pair<int,int> PII;
int dist[N];
int h[N],e[N],w[N],ne[N],idx;
bool st[N];
int n,m;
void add(int a,int b,int c){
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx;
idx++;
}
int dijkstra(){
memset(dist,0x3f,sizeof dist);
dist[1]=0;
priority_queue<PII,vector<PII>,greater<PII>> heap;
heap.push({0,1});//距离和编号
//遍历大部分的边
while(heap.size()){
auto t=heap.top();//O(m) * O(1) -> O(m)
heap.pop();
int distance=t.first,id=t.second;
if(st[id])continue;
st[id]=true;//O(m) * O(1) -> O(m)
for(int i=h[id];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]>dist[id]+w[i]){
dist[j]=dist[id]+w[i];
heap.push({dist[j],j});
// 堆的插入操作时间复杂度是 O(log(n))
// O(m) * O(log(n)) -> O(mlog(n))
}
}
}
if(dist[n]!=0x3f3f3f3f)return dist[n];
else return -1;
}
int main(){
memset(h,-1,sizeof h);
cin>>n>>m;
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
cout<<dijkstra();
return 0;
}
bellman-ford
1.有边数限制的最短路
图中可能存在重边和自环, 边权可能为负数。
求出从1号点到n号点的最多经过 k 条边的最短距离
注意:图中可能 存在负权回路 。


#include<bits/stdc++.h>
using namespace std;
const int N=510,M=1e4+10;
int n,m,k;
int dist[N];
int backup[N];
struct edge{
int a,b,w;
}edges[M];
void bellman_ford(){
memset(dist,0x3f,sizeof dist);
dist[1]=0;
for(int i=0;i<k;i++){
memcpy(backup,dist,sizeof dist);
for(int j=0;j<m;j++){
auto e=edges[j];
int a=e.a,b=e.b,w=e.w;
//加入每条边去松弛每个点到起点的距离
dist[b]=min(dist[b],backup[a]+w);
}
}
}
int main(){
cin>>n>>m>>k;
for(int i=0;i<m;i++){
int a,b,w;
cin>>a>>b>>w;
edges[i]={a,b,w};
}
bellman_ford();
if(dist[n]>0x3f3f3f3f/2)cout<<"impossible"<<endl;
else cout<<dist[n];
return 0;
}
spfa
1.spfa求最短路
cv大佬的分析总结(原文链接)
Bellman_ford算法会遍历所有的边,但是有很多的边遍历了其实没有什么意义,我们只用遍历那些到源点距离变小的点所连接的边即可,只有当一个点的前驱结点更新了,该节点才会得到更新;因此考虑到这一点,我们将创建一个队列每一次加入距离被更新的结点。
值得注意的是:
1) st数组的作用:判断当前的点是否已经加入到队列当中了;已经加入队列的结点就不需要反复的把该点加入到队列中了,就算此次还是会更新到源点的距离,那只用更新一下数值而不用加入到队列当中。
即便不使用st数组最终也没有什么关系,但是使用的好处在于可以提升效率。
2) SPFA算法看上去和Dijstra算法长得有一些像但是其中的意义还是相差甚远的:
1)⭐️Dijkstra算法中的st数组保存的是当前确定了到源点距离最小的点,且一旦确定了最小那么就不可逆了(不可标记为true后改变为false);SPFA算法中的st数组仅仅只是表示的当前发生过更新的点,且spfa中的st数组可逆(可以在标记为true之后又标记为false)。顺带一提的是BFS中的st数组记录的是当前已经被遍历过的点。
2)⭐️Dijkstra算法里使用的是优先队列保存的是当前未确定最小距离的点,目的是快速的取出当前到源点距离最小的点;SPFA算法中使用的是队列(你也可以使用别的数据结构),目的只是记录一下当前发生过更新的点。
3) ⭐️Bellman_ford算法里最后return-1的判断条件写的是dist[n]>0x3f3f3f3f/2;而spfa算法写的是dist[n]==0x3f3f3f3f;其原因在于Bellman_ford算法会遍历所有的边,因此不管是不是和源点连通的边它都会得到更新;但是SPFA算法不一样,它相当于采用了BFS,因此遍历到的结点都是与源点连通的,因此如果你要求的n和源点不连通,它不会得到更新,还是保持的0x3f3f3f3f。
4) ⭐️ Bellman_ford算法可以存在负权回路,是因为其循环的次数是有限制的因此最终不会发生死循环;但是SPFA算法不可以,由于用了队列来存储,只要发生了更新就会不断的入队,因此假如有负权回路请你不要用SPFA否则会死循环。
5) ⭐️由于SPFA算法是由Bellman_ford算法优化而来,在最坏的情况下时间复杂度和它一样即时间复杂度为 O(nm),假如题目时间允许可以直接用SPFA算法去解Dijkstra算法的题目。(好像SPFA有点小小万能的感觉?)
6) ⭐️求负环一般使用SPFA算法,方法是用一个cnt数组记录每个点到源点的边数,一个点被更新一次就+1,一旦有点的边数达到了n那就证明存在了负环。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int h[N],e[N],ne[N],w[N],idx;
int n,m;
int dist[N];
int st[N];
void add(int a,int b,int c){
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx;
idx++;
}
void spfa(){
memset(dist,0x3f,sizeof dist);
dist[1]=0;
queue<int> q;
q.push(1);
st[1]=true;//标记在不在队列中
while(q.size()){
auto t=q.front();
q.pop();
//从队列中取出来之后该节点st被标记为false,代表之后该节点如果发生更新可再次入队
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]>dist[t]+w[i]){
dist[j]=dist[t]+w[i];
if(!st[j]){//当前已经加入队列的结点,无需再次加入队列,即便发生了更新也只用更新数值即可,重复添加降低效率
q.push(j);
st[j]=true;
}
}
}
}
}
int main(){
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
spfa();
if(dist[n]==0x3f3f3f3f)puts("impossible");
else cout<<dist[n]<<endl;
return 0;
}
2.spfa判断负环
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int h[N],e[N],ne[N],w[N],idx;
int n,m;
int dist[N],cnt[N];
int st[N];
void add(int a,int b,int c){
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx;
idx++;
}
bool spfa(){
//这里不需要初始化dist数组为 正无穷/初始化的原因是: 如果存在负环, 那么dist不管初始化为多少, 都会被更新
queue<int> q;
//不仅仅是1了, 因为点1可能到不了有负环的点, 因此把所有点都加入队列
for(int i=1;i<=n;i++){
q.push(i);
st[i]=true;//标记在不在队列中
}
while(q.size()){
auto t=q.front();
q.pop();
//从队列中取出来之后该节点st被标记为false,代表之后该节点如果发生更新可再次入队
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]>dist[t]+w[i]){
dist[j]=dist[t]+w[i];
cnt[j]=cnt[t]+1;//cnt记录经过的边数 如果大于n了说明存在负环
if(cnt[j]>n)return true;
if(!st[j]){//当前已经加入队列的结点,无需再次加入队列,即便发生了更新也只用更新数值即可,重复添加降低效率
q.push(j);
st[j]=true;
}
}
}
}
return false;
}
int main(){
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
if(spfa())puts("Yes");
else puts("No");
return 0;
}
下图为和spfa板子的区别,多加了个cnt记录经过的边 如果大于n了说明存在负环
cnt[x]表示当前从1~x的最短路的边数
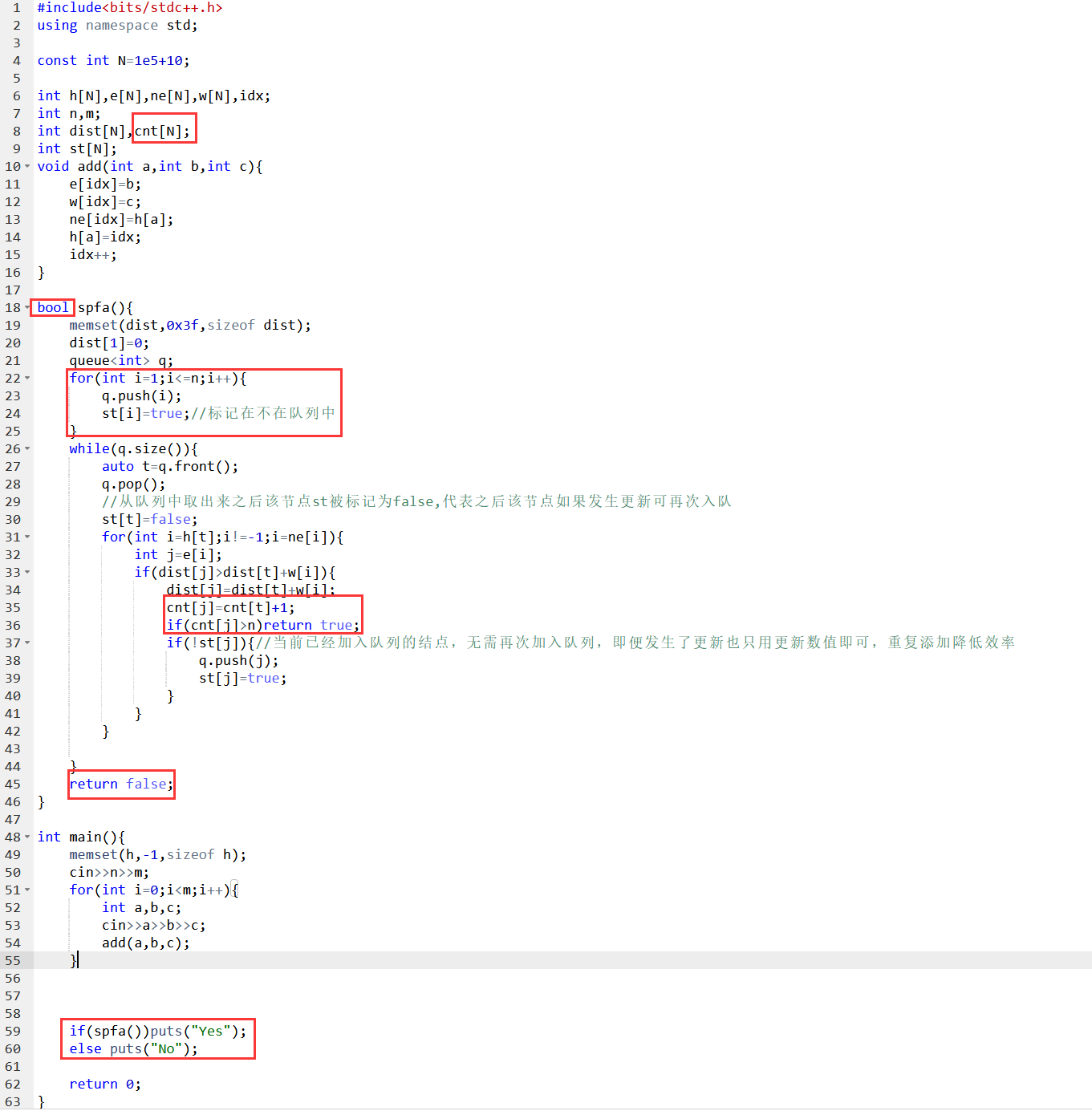
这里不需要初始化dist数组为 正无穷/初始化的原因是: 如果存在负环, 那么dist不管初始化为多少, 都会被更新
memset(dist,0x3f,sizeof dist);
dist[1]=0;
不仅仅是1了, 因为点1可能到不了有负环的点, 因此把所有点都加入队列
for(int i=1;i<=n;i++){
q.push(i);
st[i]=true;
}
Floyd
1.Floyd求最短路 多元最短路
#include<bits/stdc++.h>
using namespace std;
const int N=210;
int n,m,Q;
int d[N][N];
void floyd(){
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}
}
}
}
int main(){
cin>>n>>m>>Q;
memset(d,0x3f,sizeof d);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==j)d[i][j]=0;
}
}
while(m--){
int a,b,w;
cin>>a>>b>>w;
d[a][b]=min(d[a][b],w);
}
floyd();
while(Q--){
int a,b;
cin>>a>>b;
if(d[a][b]>=0x3f3f3f3f/2)puts("impossible");
else cout<<d[a][b]<<endl;
}
return 0;
}
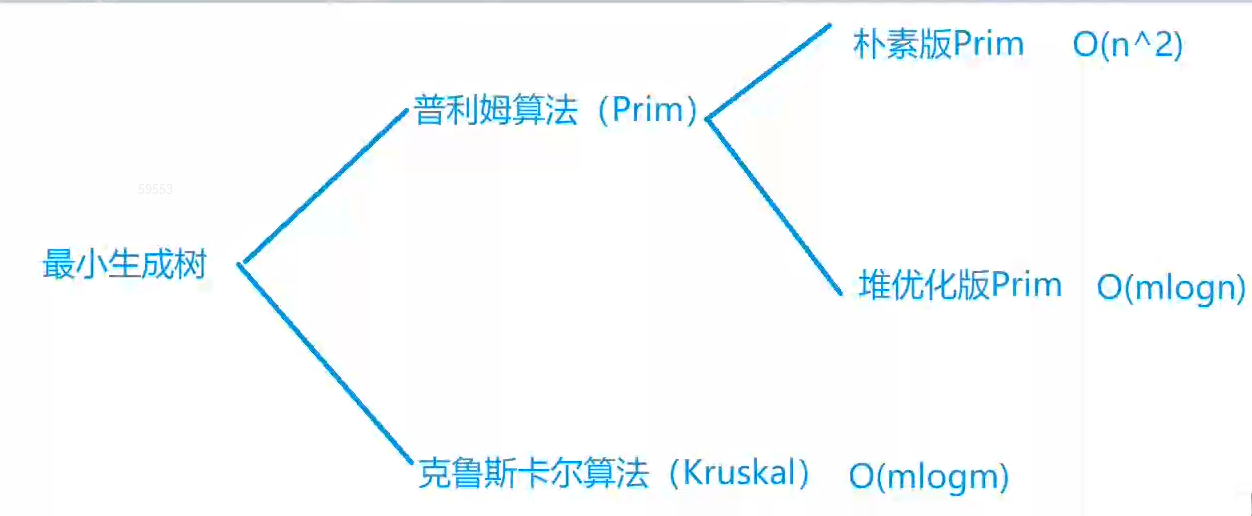
最小生成树
总结
prim
1.Prim算法求最小生成树
prim 算法采用的是一种贪心的策略。
每次将离连通部分的最近的点和点对应的边加入的连通部分,连通部分逐渐扩大,最后将整个图连通起来,并且边长之和最小。
联系:Dijkstra算法是更新到起始点的距离,Prim是更新到集合S的距离
#include<bits/stdc++.h>
using namespace std;
const int N=510;
int dist[N];
int st[N];
int d[N][N];
int pre[N];
int n,m;
int prim(){
memset(dist,0x3f,sizeof dist);
int res=0;
for(int i=0;i<n;i++){//每次循环选出一个点加入到生成树
int t=-1;
for(int j=1;j<=n;j++){
if(!st[j]&&(t==-1||dist[j]<dist[t])){
t=j;
}
}
st[t]=true;
if(i&&dist[t]==0x3f3f3f3f)return 0x3f3f3f3f;//如果不是第一次 且找不到
if(i)res+=dist[t];
for(int j=1;j<=n;j++){
if(!st[j]&&dist[j]>d[t][j])//从t到节点j的距离小于原来距离,则更新。
{
dist[j]=d[t][j];//更新各个点到集合的距离
//pre[j] = t;//从t到j的距离更短,j的前驱变为t
}
}
}
return res;
}
/*
void getPath()//输出各个边
{
for(int i = n; i > 1; i--)//n 个节点,所以有 n-1 条边。
{
cout << i <<" " << pre[i] << " "<< endl;// i 是节点编号,pre[i] 是 i 节点的前驱节点。他们构成一条边。
}
}*/
int main(){
memset(d,0x3f,sizeof d);
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
d[a][b]=d[b][a]=min(d[a][b],c);
}
int t=prim();
if(t>0x3f3f3f3f/2)puts("impossible");
else cout<<t;
//getPath();//输出路径
return 0;
}
Kruskal
1.Kruskal算法求最小生成树

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int p[N];
int n,m;
struct edge{
int a,b,w;
}edges[N];
bool cmp(const edge &x,const edge &y){
return x.w<y.w;
}
int find(int x){
if(p[x]!=x)p[x]=find(p[x]);
return p[x];
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)p[i]=i;
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
edges[i]={a,b,c};
}
sort(edges,edges+m,cmp);
int res=0,cnt=0;
for(int i=0;i<m;i++){
int a=edges[i].a,b=edges[i].b,w=edges[i].w;
if(find(a)!=find(b)){
p[find(a)]=find(b);
cnt+=1;
res+=w;
}
}
if(cnt<n-1)puts("impossible");
else cout<<res;
return 0;
}
二分图
总结

染色法判定二分图
1.染色法判定二分图

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=2e5+10;
int h[N],e[M],ne[M],idx;
int color[N];
int n,m;
void add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx;
idx++;
}
bool dfs(int u,int c){
color[u]=c;
for(int i=h[u];i!=-1;i=ne[i]){//尝试染链接边的颜色
int j=e[i];
if(color[j]==c)return false;//如果染过颜色且和c相同
if(!color[j]){//如果color[j]没有染过色
if(dfs(j,3-c)==false)return false;//如果不可以将j成功染色
}
}
return true;
}
int main(){
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
bool flag=true;
for(int i=1;i<=n;i++){
if(!color[i]){
flag=dfs(i,1);//如果dfs返回false 说明出现矛盾
if(flag==false)break;
}
}
if(flag==true)puts("Yes");
else puts("No");
return 0;
}
匈牙利算法
算法描述:如果你想找的妹子已经有了男朋友,你就去问问她男朋友有没有备胎,把这个让给我好吧.
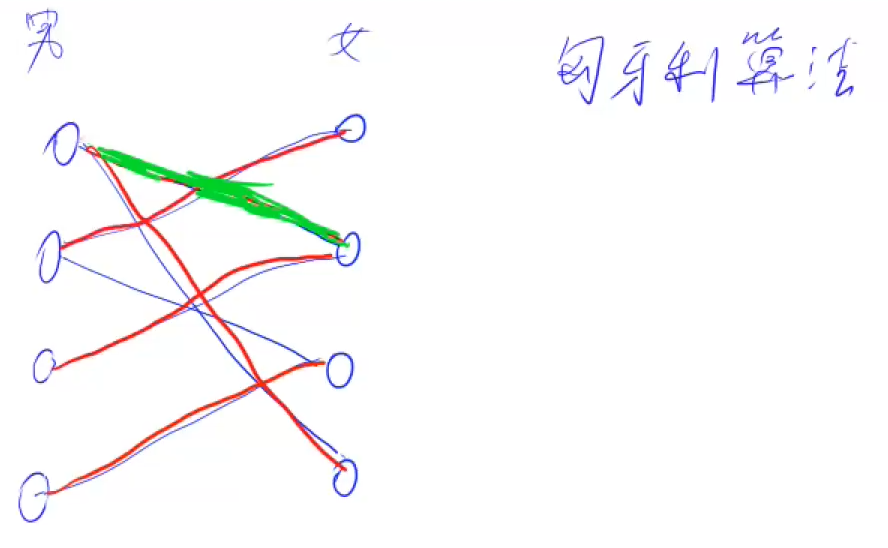
1.二分图的最大匹配
#include<bits/stdc++.h>
using namespace std;
const int N=510,M=1e5+10;
int n1,n2,m;
int h[N],e[M],ne[M],idx;
int match[N];//女生匹配的男生
int st[N];//st[]数组我称为临时预定数组,st[j]=a表示一轮模拟匹配中,女孩j被男孩a预定了。
void add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx;
idx++;
}
//find函数的作用是用来判断,如果加入x来参与模拟配对,会不会使匹配数增多
bool find(int u){
for(int i=h[u];i!=-1;i=ne[i]){//遍历自己喜欢的女孩
int j=e[i];
if(!st[j]){//如果在这一轮模拟匹配中,这个女孩尚未被预定
st[j]=true;//那u就预定这个女孩
//如果女孩j没有男朋友,或者她原来的男朋友能够预定其它喜欢的女孩。配对成功,更新match
if(match[j]==0||find(match[j])){
match[j]=u;
return true;
}
}
}
//自己中意的全部都被预定了。配对失败。
return false;
}
int main(){
memset(h,-1,sizeof h);
cin>>n1>>n2>>m;
while(m--){
int a,b;
scanf("%d%d",&a,&b);
add(a,b);//存边只存一边就行了,虽然是无向图。
}
int res=0;//记录最大匹配
for(int i=1;i<=n1;i++){
//因为每次模拟匹配的预定情况都是不一样的所以每轮模拟都要初始化
memset(st,false,sizeof st);
if(find(i)){
res++;
}
}
cout<<res;
}


求关注
(´ ▽`).。o♡