基础-2.数据结构二刷小结

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

基础-2.数据结构二刷小结

作者：

lu1zero9 , 2022-03-24 10:53:44 , 所有人可见 , 阅读 183

0

2

2.数据结构

单链表

1.单链表(初始化、头插、插入、删除、遍历)

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;

int idx,e[N],ne[N],head;

void init(){
    head=-1;
    idx=0;
}

void add_to_head(int x){
    e[idx]=x;
    ne[idx]=head;
    head=idx;
    idx++;
}

void add(int k,int x){
    e[idx]=x;
    ne[idx]=ne[k];
    ne[k]=idx;
    idx++;
}

void del(int k){
    ne[k]=ne[ne[k]];
}

int main(){
    int n;
    cin>>n;
    init();

    while(n--){
        char op;
        cin>>op;
        if(op=='H'){
            int x;
            cin>>x;
            add_to_head(x);
        }else if(op=='D'){
            int k;
            cin>>k;
            if(k==0)head=ne[head];
            else del(k-1);
        }else if(op=='I'){
            int k,x;
            cin>>k>>x;
            add(k-1,x);
        }
    }
    for(int i=head;i!=-1;i=ne[i])cout<<e[i]<<" ";

    return 0;
}

双链表

1.双链表(初始化、左右两端插入、插入、删除、遍历)

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;

int l[N],r[N],e[N],idx;
// 0是左端点，1是右端点
void init(){
    r[0]=1;
    l[1]=0;
    idx=2;
}
// 在节点k的右边插入一个数x
void add(int k,int x){
    e[idx]=x;
    r[idx]=r[k];
    l[idx]=l[r[k]];
    r[k]=idx;
    l[r[idx]]=idx;
    idx++;
}

void remove(int k){
    r[l[k]]=r[k];
    l[r[k]]=l[k];
}

int main(){
    int n;
    cin>>n;
    init();
    while(n--){
        string op;
        cin>>op;
        if(op=="L"){
            int x;
            cin>>x;
            add(0,x);
        }else if(op=="R"){
            int x;
            cin>>x;
            add(l[1],x);
        }else if(op=="D"){
            int k;
            cin>>k;
            remove(k+1);
        }else if(op=="IL"){
            int k,x;
            cin>>k>>x;
            add(l[k+1],x);
        }else if(op=="IR"){
            int k,x;
            cin>>k>>x;
            add(k+1,x);
        }
    }

    for(int i=r[0];i!=1;i=r[i])cout<<e[i]<<" ";
    return 0;
}

栈

1.模拟栈(定义、入栈、出栈、判断是否为空、查看栈顶元素)

#include<bits/stdc++.h>
 using namespace std;

 const int N=1e5+10;

 int st[N];
 int top=-1;

 int main(){
     int n;
     cin>>n;
     while(n--){
         string op;
         cin>>op;
         if(op=="push"){
             int x;
             cin>>x;
             st[++top]=x;
         }else if(op=="pop"){
             --top;
         }else if(op=="empty"){
             if(top==-1)puts("YES");
             else puts("NO");
         }else if(op=="query"){
             cout<<st[top]<<endl;
         }
     }
     return 0;
 }

2.表达式求值(中缀表达式正常表达式)

#include<bits/stdc++.h>
using namespace std;

stack<int> num;
stack<char> op;

//优先级表
unordered_map<char,int> h{{'+',1},{'-',1},{'*',2},{'/',2}};

void eval(){
    int b=num.top();//第二个操作数
    num.pop();
    int a=num.top();//第一个操作数
    num.pop();
    int ch=op.top();//运算符
    op.pop();

    int res=0;
    if(ch=='+')res=a+b;
    else if(ch=='-')res=a-b;
    else if(ch=='*')res=a*b;
    else res=a/b;

    num.push(res);
}

int main(){
    string str;//读入表达式
    cin>>str;

    for(int i=0;i<str.size();i++){
        //isdigit判断字符型是否是数字
        if(isdigit(str[i])){//数字入栈
            int x=0,j=i;
            while(j<str.size()&&isdigit(str[j])){
                x=x*10+str[j]-'0';
                j++;
            }
            num.push(x);
            i=j-1;
        }else if(str[i]=='('){
            //左括号无优先级，直接入栈
            op.push(str[i]);
        }else if(str[i]==')'){
            //括号特殊，遇到左括号直接入栈，遇到右括号计算括号里面的
            while(op.top()!='(')eval();//一直计算到左括号
            op.pop();
        }else{
            //待入栈运算符优先级低，则先计算
            while(op.size()&&h[op.top()]>=h[str[i]])eval();
            op.push(str[i]);//操作符入栈
        }
    }
    while(op.size())eval();//剩余的进行计算
    cout<<num.top()<<endl;//输出结果
    return 0;
}

队列

1.模拟队列(定义队头和队尾、插入、删除、查询队头元素)

#include<bits/stdc++.h>
using namespace std;

int m;
const int N=1e5+10;
int q[N];
int hh=0,tt=-1;
int main(){
    cin>>m;
    while(m--){
        string op;
        cin>>op;
        if(op=="push"){
            int x;
            cin>>x;
            q[++tt]=x;
        }else if(op=="pop"){
            hh++;
        }else if(op=="empty"){
            if(hh>tt)puts("YES");
            else puts("NO");
        }else if(op=="query"){
            cout<<q[hh]<<endl;
        }
    }
    return 0;
}

单调栈

1.单调栈(找到数列中每个数左边第一个比其小的数)

给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;
int stk[N],tt=0;

int main(){
    int n;
    cin>>n;
    while(n--){
        int x;
        cin>>x;
        while(tt&&stk[tt]>=x)tt--;
        if(tt)cout<<stk[tt]<<" ";
        else cout<<-1<<" "; 
        stk[++tt]=x;
    }
    return 0;
}

单调队列

1.单调队列求滑动窗口中最大最小值

最小值和最大值分开来做，两个for循环完全类似，都做以下四步：

1.解决队首已经出窗口的问题;
2.解决队尾与当前元素a[i]不满足单调性的问题;
3.将当前元素下标加入队尾;
4.如果满足条件则输出结果;

#include<bits/stdc++.h>
using namespace std;

const int N=1e6+10;

int q[N]; //q存储下标
int a[N];
int main(){
    //hh tt

    int n,k;
    cin>>n>>k;
    for(int i=0;i<n;i++)scanf("%d",&a[i]);
    int hh=0,tt=-1;
    for(int i=0;i<n;i++){
        if(hh<=tt&&i-k+1>q[hh])hh++;//维护队头
        while(hh<=tt&&a[q[tt]]>=a[i])tt--;//若队尾不单调，tt减1

        q[++tt]=i;//将下标加到队尾
        if(i>=k-1)printf("%d ",a[q[hh]]);// 满足窗口中有k个值 可以输出结果
    }
    puts("");

    hh=0,tt=-1;
    for(int i=0;i<n;i++){
        if(hh<=tt&&i-k+1>q[hh])hh++;
        while(hh<=tt&&a[q[tt]]<=a[i])tt--;
        q[++tt]=i;
        if(i>=k-1)printf("%d ",a[q[hh]]);
    }
}

KMP字符串匹配算法

1.KMP字符串匹配、Next数组

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10,M=1e6+10;

char p[N],s[M];
int ne[N];
int main(){
    int n,m;
    cin>>n>>p+1>>m>>s+1;

    //求ne数组
    for(int i=2,j=0;i<=n;i++){
        while(j&&p[i]!=p[j+1])j=ne[j];
        if(p[i]==p[j+1])j++;
        ne[i]=j;
    }

    //模式匹配
    for(int i=1,j=0;i<=m;i++){
        while(j&&s[i]!=p[j+1])j=ne[j];
        if(s[i]==p[j+1])j++;
        if(j==n){
            cout<<i-n<<" ";
            j=ne[j];
        }
    }
    return 0;
}

Trie前缀树/字典树

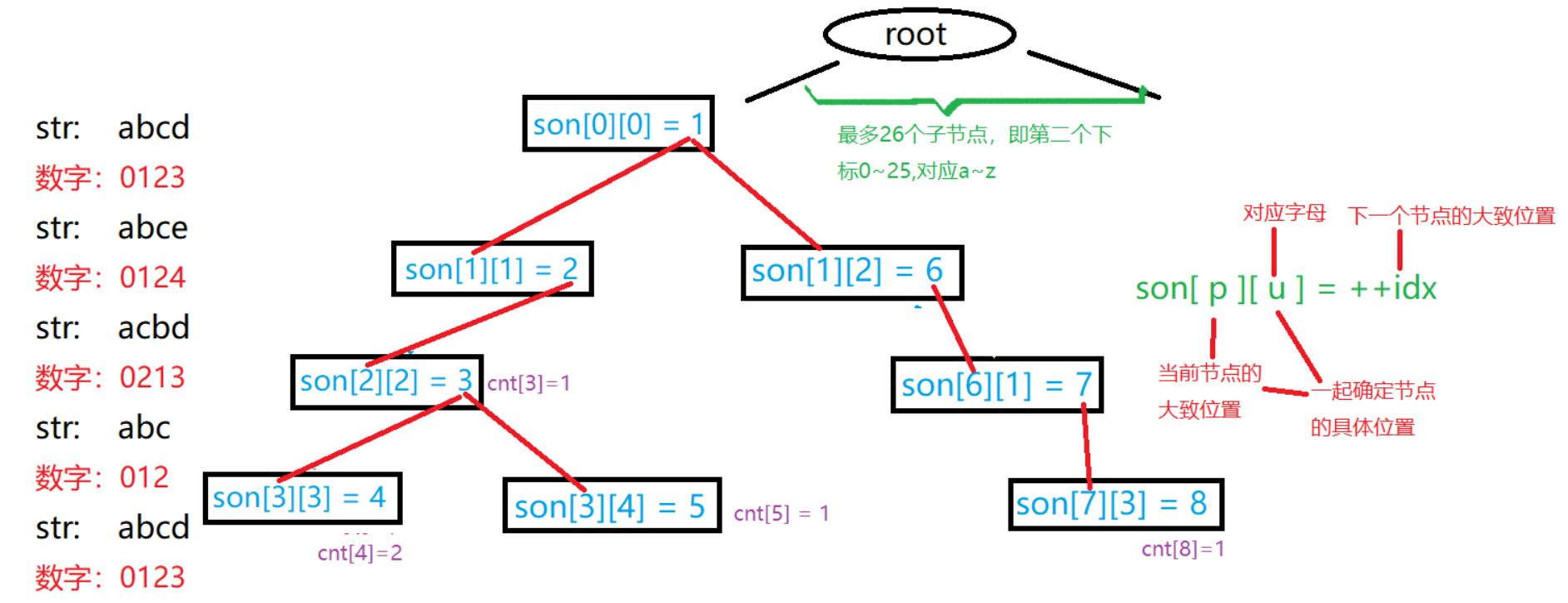
1.Trie字符串统计(高效存储和查找字符串集合)

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;

int son[N][26],cnt[N],idx;
//son[][]存储子节点的位置，分支最多26条；
//cnt[]存储以某节点结尾的字符串个数（同时也起标记作用）
//idx表示当前要插入的节点是第几个,每创建一个节点值+1
void insert(char str[]){
    int p=0;//类似指针，指向当前节点
    for(int i=0;str[i];i++){
        int u=str[i]-'a';//将字母转化为数字
        if(!son[p][u])son[p][u]=++idx;//该节点不存在，创建节点
        p=son[p][u]; //使“p指针”指向下一个节点
    }
    cnt[p]++;//结束时的标记，也是记录以此节点结束的字符串个数
}

int query(char str[]){
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u])return 0; //该节点不存在，即该字符串不存在
        p=son[p][u];
    }
    return cnt[p];//返回字符串出现的次数
}

int main(){
    int n;
    cin>>n;
    while(n--){
        char str[N];
        char op;
        cin>>op>>str;
        if(op=='I')insert(str);
        else cout<<query(str)<<endl;
    }
    return 0;
}

2.Tire存储多个整数求最大异或对

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;
int a[N];
int son[N*31][2];
int res;
int idx;

void insert(int x){
    int p=0;
    for(int i=30;i>=0;i--){
        int u=x>>i&1;
        if(!son[p][u])son[p][u]=++idx;
        p=son[p][u];
    }
}

int search(int x){
    int p=0;
    int t=0;
    for(int i=30;i>=0;i--){
        int u=x>>i&1;
        if(son[p][!u]){
            p=son[p][!u];
            t=t*2+1;
        }else{
            p=son[p][u];
            t=t*2+0;
        }
    }
    return t;
}
int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++)scanf("%d",&a[i]);

    for(int i=0;i<n;i++){
        insert(a[i]);
        //search(a[i])在这查找的是a[i]值的最大与或值
        int t=search(a[i]);

        res=max(res,t);
    }
    cout<<res;
    return 0;
}

并查集

1.并查集模板(初始化、合并集合、查询是否为同一集合)

#include<bits/stdc++.h>
using namespace std;

const int N=2e5+10;

int n,m;
int p[N];
int find(int x){
    if(p[x]!=x)p[x]=find(p[x]);
    return p[x];
}

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)p[i]=i;
    while(m--){
        char op;
        int a,b;
        cin>>op>>a>>b;
        if(op=='M'){
            p[find(a)]=find(b);
        }else{
            if(find(a)==find(b))puts("Yes");
            else puts("No");
        }
    }
    return 0;
}

2.并查集记录连通块中点的数量

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;

int p[N],s[N];
int n,m;

int find(int x){
    if(p[x]!=x)p[x]=find(p[x]);
    return p[x];
}

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)p[i]=i,s[i]=1;
    while(m--){
        string op;
        cin>>op;
        if(op=="C"){
            int a,b;
            cin>>a>>b;
            if(find(a)==find(b))continue;
            else{
                s[find(b)]+=s[find(a)];
                p[find(a)]=find(b);
            }
        }else if(op=="Q1"){
            int a,b;
            cin>>a>>b;
            if(find(a)==find(b))puts("Yes");
            else puts("No");
        }else{
            int a;
            cin>>a;
            cout<<s[find(a)]<<endl;
        }
    }
    return 0;
}

3.带权并查集之食物链

思路：只要x和y有关系，那么x和y就属于同一个集合(不管属于什么类别)，通过他们与根结点的距离就可以知道二者的关系。

三种关系：

两个数组的定义：

p[]:父节点,
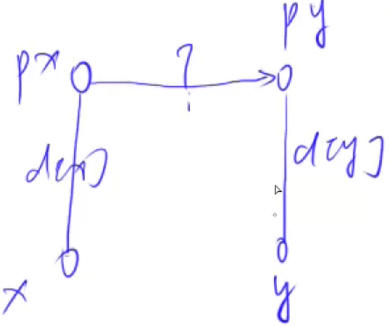
d[]:到父节点（不是根节点）的距离(初始是1，随着路径压缩会逐渐增大)

只能获得点到其直接父节点的距离。路径压缩和更新边权的时候也是这样。

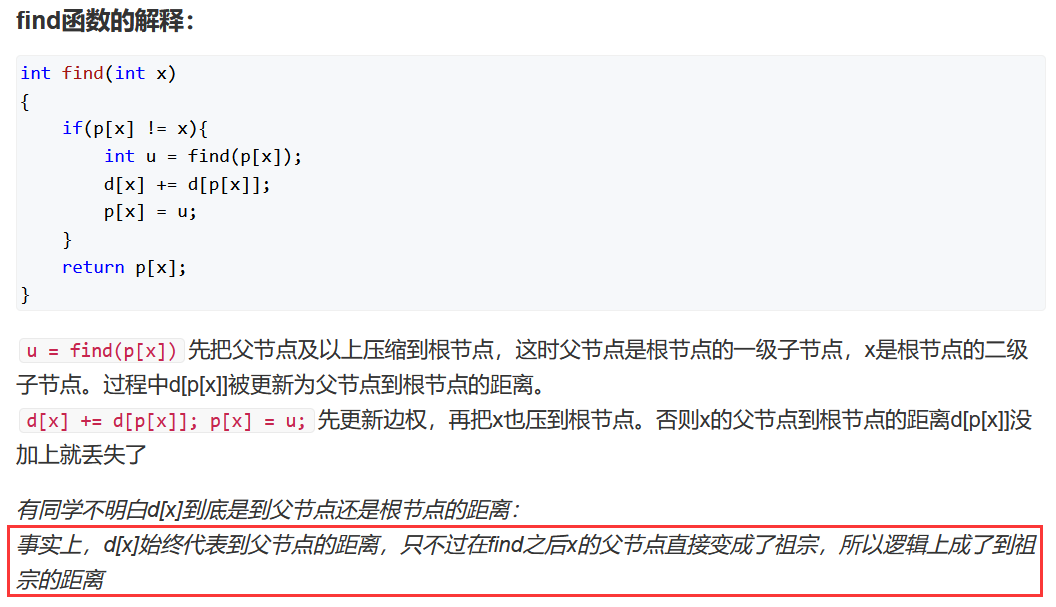
x与y关系是同类意味着d[x]+d[px]-d[y])%3 == 0，故有d[px] = d[y] - d[x];

x与y的关系是x吃y意味着d[x]-d[y]-1)%3 == 0，故有d[px] = d[y] - d[x] + 1;

#include<bits/stdc++.h>
using namespace std;

const int N=5e4+10;

int p[N],d[N];
int n,m;

int find(int x){
    if(x!=p[x]){
        int u=find(p[x]);
        d[x]+=d[p[x]];
        p[x]=u;
    }
    return p[x];
}

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)p[i]=i;

    int res=0;
    while(m--){
        int t,x,y;
        cin>>t>>x>>y;
        if(x>n||y>n){//当前的话中X或Y比N大,就是假话;
            res++;
        }else{
            int px=find(x),py=find(y);
            if(t==1){// t=1，则表示X和Y是同类。
                //px==py 判断是否在集合当中 且不为同一类
                if(px==py&&(d[x]-d[y])%3!=0){
                    res++;
                }else if(px!=py){
                    p[px]=py;
                    d[px]=d[y]-d[x];
                }
            }else{//t=2,则表示X吃Y
                //判断是否在集合当中 且x能吃y
                if(px==py&&(d[x]-d[y]-1)%3!=0)res++;
                else if(px!=py){
                    p[px]=py;
                    d[px]=d[y]-d[x]+1;
                }
            }
        }
    }
    cout<<res;
    return 0;

}

堆

1.堆排序

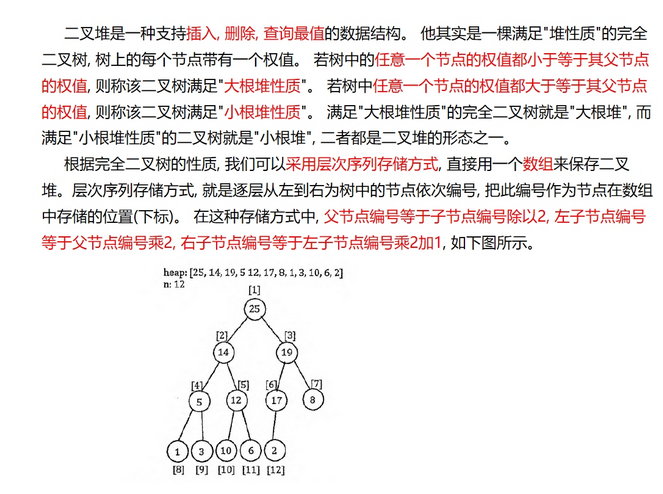
以小根堆为例子

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;

int h[N],cnt;

void down(int u){
    int t=u;
    if(2*u<=cnt&&h[2*u]<h[u])t=2*u;
    if(2*u+1<=cnt&&h[2*u+1]<h[t])t=2*u+1;
    if(t!=u){
        swap(h[t],h[u]);
        down(t);
    }
}

int main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)scanf("%d",&h[i]);
    cnt=n;
    for(int i=cnt/2;i>=1;i--)down(i);

    while(m--){
        cout<<h[1]<<" ";
        h[1]=h[cnt];
        cnt--;
        down(1);
    }
    return 0;
}

https://www.acwing.com/solution/content/29416/ 详细介绍题解

2.模拟堆

https://www.acwing.com/solution/content/5661/详细介绍题解

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;

int h[N],ph[N],hp[N],cnt;

void heap_swap(int a, int b)
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u){
    int t=u;
    if(2*u<=cnt&&h[2*u]<h[u])t=2*u;
    if(2*u+1<=cnt&&h[2*u+1]<h[t])t=2*u+1;
    if(t!=u){
        heap_swap(t,u);
        down(t);
    }
}

void up(int u){
    while(u/2&&h[u]<h[u/2]){
        heap_swap(u,u/2);
        u/=2;
    }
}

int main(){
    int n,idx=0;
    cin>>n;
    while(n--){
        string op;
        cin>>op;
        int k,x;
        if(op=="I"){//I x，插入一个数 x;
            scanf("%d",&x);
            cnt++;
            idx++;
            ph[idx]=cnt,hp[cnt]=idx;
            h[cnt]=x;
            up(cnt);
        }else if(op=="PM"){//PM 输出当前集合中的最小值；
            cout<<h[1]<<endl;
        }else if(op=="DM"){//DM 删除当前集合中的最小值
            heap_swap(1,cnt);
            cnt--;
            down(1);
        }else if(op=="D"){//删除第k个插入的数；
            scanf("%d",&k);
            k=ph[k];
            heap_swap(k,cnt);
            cnt--;
            up(k);
            down(k);
        }else{//修改第k个插入的数，将其变为x；
            scanf("%d%d",&k,&x);
            h[ph[k]]=x;
            up(ph[k]);
            down(ph[k]);
        }
    }
    return 0;
}

哈希表

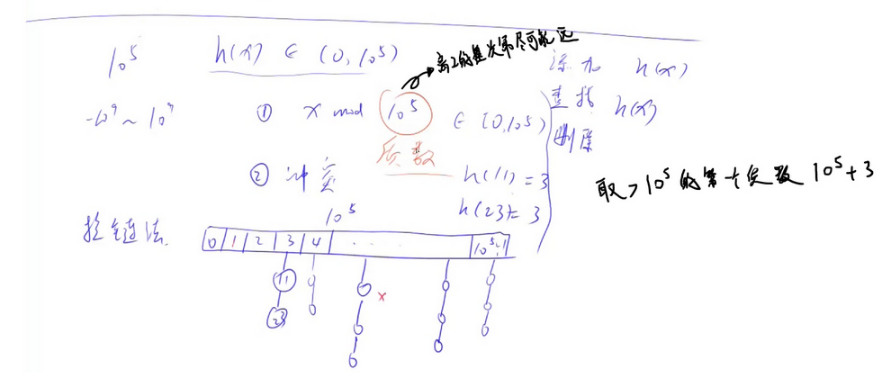
1.模拟散列表(拉链法)

#include<bits/stdc++.h>
using namespace std;

//拉链法 
const int N=100003;//大于1e5的第一个质数

int h[N],e[N],ne[N],idx;

void insert(int x){
    int k=(x%N+N)%N;
    e[idx]=x;
    ne[idx]=h[k];
    h[k]=idx++;
}

bool query(int x){
    int k=(x%N+N)%N;
    for(int i=h[k];i!=-1;i=ne[i]){
        if(e[i]==x){
            return true;
        }
    }
    return false;
}

int main(){
    int n;
    cin>>n;
    memset(h,-1,sizeof h);
    while(n--){
        string op;
        int x;
        cin>>op>>x;
        if(op=="I"){
            insert(x);
        }else{
            if(query(x))puts("Yes");
            else puts("No");
        }
    }
    return 0;
}

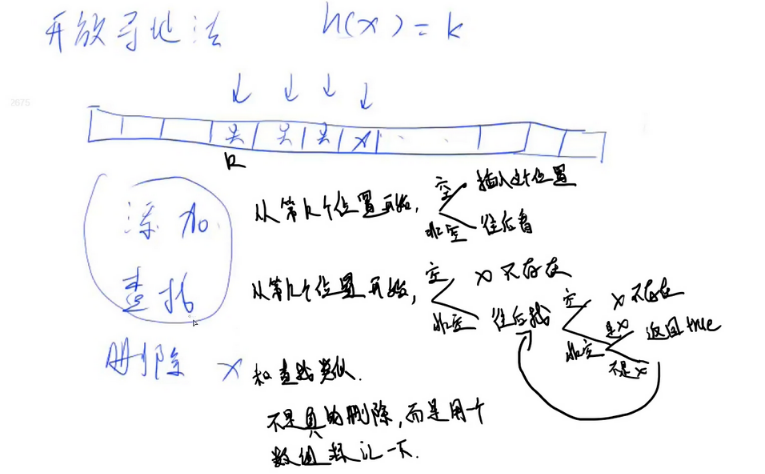
2.模拟散列表(开放寻址法)

#include<bits/stdc++.h>
using namespace std;

//拉链法 
//开放寻址法一般开 数据范围的 2~3倍, 这样大概率就没有冲突了
const int N=200003;//大于2e5的第一个质数
const int null=0x3f3f3f3f;//规定空指针为 null 0x3f3f3f3f
int h[N];

int find(int x){
    int k=(x%N+N)%N;
    while(h[k]!=null&&h[k]!=x){
        k++;
        if(k==N)k=0;
    }
    return k;//如果这个位置是空的, 则返回的是他应该存储的位置
}

int main(){
    int n;
    cin>>n;
    memset(h,0x3f,sizeof h);
    while(n--){
        string op;
        int x;
        cin>>op>>x;
        int k=find(x);
        if(op=="I"){
            h[k]=x;
        }else{
            if(h[k]!=null)puts("Yes");
            else puts("No");
        }
    }
    return 0;
}

3.字符串哈希

#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;

typedef unsigned long long ULL;
const int N=1e5+10,P=131;
ULL h[N],p[N];

//h[i]   前i个字符的hash值
//字符串变成一个p进制数字，体现了字符+顺序，(需要确保不同的字符串对应不同的数字)
//P=131或13331  Q=2^64  (在99%的情况下不会出现冲突)

//使用场景：两个字符串的子串是否相同

ULL query(int l,int r){
    return h[r]-h[l-1]*p[r-l+1];
}

int main(){
    int n,m;
    cin>>n>>m; //n为字符串长度 m为询问次数
    string x;
    cin>>x;
    //字符串从1开始编号,h[1]为前一个字符的哈希值
    p[0]=1;
    for(int i=0;i<n;i++){
        p[i+1]=p[i]*P;
        h[i+1]=h[i]*P+x[i]; //前缀求整个字符串的哈希值
    }

    while(m--){
        int l1,r1,l2,r2;
        cin>>l1>>r1>>l2>>r2;
        if(query(l1,r1)==query(l2,r2))puts("Yes");
        else puts("No");
    }
    return 0;
}

0 评论

App 内打开

基础-2.数据结构二刷小结

2.数据结构

单链表

1.单链表(初始化、头插、插入、删除、遍历)

双链表

1.双链表(初始化、左右两端插入、插入、删除、遍历)

栈

1.模拟栈(定义、入栈、出栈、判断是否为空、查看栈顶元素)

2.表达式求值(中缀表达式 正常表达式)

队列

1.模拟队列(定义队头和队尾、插入、删除、查询队头元素)

单调栈

1.单调栈(找到数列中每个数左边第一个比其小的数)

单调队列

1.单调队列求滑动窗口中最大最小值

KMP字符串匹配算法

1.KMP字符串匹配、Next数组

Trie前缀树/字典树

1.Trie字符串统计(高效存储和查找字符串集合)

2.Tire存储多个整数求最大异或对

并查集

1.并查集模板(初始化、合并集合、查询是否为同一集合)

2.并查集记录连通块中点的数量

3.带权并查集之食物链

堆

1.堆排序

2.模拟堆

哈希表

1.模拟散列表(拉链法)

2.模拟散列表(开放寻址法)

3.字符串哈希

0 评论

2.表达式求值(中缀表达式正常表达式)