双指针算法
常常用来将(On2)的算法优化到(o(n),形式为两个指针扫描一段区间,经常使用空间换取时间
799. 最长连续不重复子序列
题目链接: https://www.acwing.com/problem/content/description/801/
题意:给定一个长度为 n 的整数序列,请找出最长的不包含重复的数的连续区间,输出它的长度。
数据范围
1≤n≤1e5
暴力代码 5/14
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],n;
bool check(int i,int j)
{
set<int> st;
for(int k=i;k<=j;k++)
{
st.insert(a[k]);
}
int z=j-i+1;
if(st.size()!=z) return false;
return true;
}
int main()
{
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
int res=-1;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(check(i,j))
{
res=max(res,j-i+1);
}
}
}
cout<<res<<endl;
return 0;
}
双指针算法优化
我们设想是否有一种方式能把双重for循环转化为单层,从而转化为O(n)的算法,我们在两层的for循环里面其实是不用循环这么多次的,因为我们的答案是a[i]和下一个a[i]出现的区间最大长度,对于在其他范围内的数,我们其实是没有必要遍历的,因此从这个角度出发,我们可以开一个数组记录一下a[i]出现的次数,指针j到i标是没有出现重复数字的区间,那么当我们的a[i]重复时,一定是与区间左端点j代表的a[j]相等,因此我们只需要在on的时间复杂度之内就能找到最大的答案
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],s[N],n,res;
int main()
{
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0,j=0;i<n;i++)
{
s[a[i]]++;
while(j<=i&&s[a[i]]>1)
{
s[a[j]]--;
j++;
}
res=max(res,i-j+1);
}
cout<<res<<endl;
return 0;
}
800. 数组元素的目标和
题目链接: https://www.acwing.com/problem/content/description/802/
题意:给定两个升序排序的有序数组 A 和 B,以及一个目标值 x。
数组下标从 0 开始。
请你求出满足 A[i]+B[j]=x 的数对 (i,j)。
数据保证有唯一解。
数据范围 1e5
暴力解 11/14
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int n,m,x;
int main()
{
cin>>n>>m>>x;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0;i<m;i++) cin>>b[i];
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
if(a[i]+b[j]==x)
{
cout<<i<<" "<<j<<endl;
return 0;
}
}
}
return 0;
}
map暴力解 AC
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int n,m,x;
map<int,int> mp;
int main()
{
cin>>n>>m>>x;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0;i<m;i++) cin>>b[i];
for(int i=0;i<m;i++) mp[b[i]]=i;
for(int i=0;i<n;i++)
{
auto it=mp.find(x-a[i]);
if(it!=mp.end())
{
cout<<i<<" "<<it->second<<endl;
return 0;
}
}
return 0;
}
二分查找 AC
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int n,m,x,r;
int main()
{
cin>>n>>m>>x;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0;i<m;i++) cin>>b[i];
for(int i=0;i<n;i++)
{
int t=x-a[i];
int l=0,r=m-1;
while(l<r)
{
int mid=l+r>>1;
if(b[mid]>=t) r=mid;
else l=mid+1;
}
if(b[l]==t)
{
cout<<i<<" "<<l<<endl;
break;
}
}
return 0;
}
双指针算法
由于两个序列是递增的,所以我们可以用两个指针一个指向a[i]开头,另一个指向b数组结尾,当a[i]的指针右移时其a[i]+b[i]是增加的,当其小于x时说明a[i]不够大,大于x说明a[j]太大了,不断缩小范围慢慢接近x,由于维护的是一段区间,所以时间复杂度为0(n)
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int n,m,x;
int main()
{
cin>>n>>m>>x;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0;i<m;i++) cin>>b[i];
for(int i=0,j=m-1;i<n;i++)
{
while(j>=0&&b[j]+a[i]>x) j--;
if(a[i]+b[j]==x)
{
printf("%d %d\n",i,j);
break;
}
}
return 0;
}
1238. 日志统计
题目链接: https://www.acwing.com/problem/content/1240/
题意:小明维护着一个程序员论坛。现在他收集了一份”点赞”日志,日志共有 N 行。
其中每一行的格式是:
ts id
表示在 ts 时刻编号 id 的帖子收到一个”赞”。
现在小明想统计有哪些帖子曾经是”热帖”。
如果一个帖子曾在任意一个长度为 D 的时间段内收到不少于 K 个赞,小明就认为这个帖子曾是”热帖”。
具体来说,如果存在某个时刻 T 满足该帖在 [T,T+D) 这段时间内(注意是左闭右开区间)收到不少于 K 个赞,该帖就曾是”热帖”。
给定日志,请你帮助小明统计出所有曾是”热帖”的帖子编号。
输入格式
第一行包含三个整数 N,D,K。
以下 N 行每行一条日志,包含两个整数 ts 和 id。
输出格式
按从小到大的顺序输出热帖 id。
每个 id 占一行。
数据范围
1≤K≤N≤105,
0≤ts,id≤105,
1≤D≤10000
暴力 蓝桥杯 62分
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
const int N=1e5+10;
bool st[N];
typedef pair<int,int> PII;
PII a[N];
int n,d,k;
int main()
{
cin>>n>>d>>k;
int max1=0;
for(int i=0;i<n;i++)
{
cin>>a[i].x>>a[i].y;
max1=max(max1,a[i].y);
}
sort(a,a+n);
for(int i=0;i<n;i++)
{
int id=a[i].y;
int t=a[i].x;
int cnt=1;
for(int j=i+1;j<n;j++)
{
if(a[j].x<t+d&&a[j].y==id) cnt++;
}
if(cnt>=k)
{
st[id]=true;
}
}
for(int i=0;i<=max1;i++)
{
if(st[i]==true)
cout<<i<<endl;
}
return 0;
}
双指针算法维护滑动窗口
思路和第一个列题一模一样,两个本质是属于滑动窗口问题,维护一段区间
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
const int N=1e5+10;
int n,d,k;
bool st[N];//记录帖子曾经是不是热帖
PII a[N];
int cnt[N];//记录帖子点赞数
int main()
{
cin>>n>>d>>k;
for(int i=0;i<n;i++) cin>>a[i].x>>a[i].y;
sort(a,a+n);
for(int i=0,j=0;i<n;i++)
{
cnt[a[i].y]++;
while(a[i].x-a[j].x>=d)//维护的是长度为d-1的滑动窗口
{
cnt[a[j].y]--;//剪掉区间末端
j++;//维护区间左端点
}
if(cnt[a[i].y]>=k) st[a[i].y]=true;//判断是不是热帖
}
for(int i=0;i<100000;i++)
{
if(st[i]==true)
{
cout<<i<<endl;
}
}
return 0;
}
AcWing 1240. 完全二叉树的权值
https://www.acwing.com/problem/content/1242/
wa 1/12
原因:没有理解完全二叉树的定义
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+10;
int n,a[N],s[N];
map<LL,int,greater<LL>> mp;
int powint(int x)
{
int n=1;
while(x--)
{
n=n*2;
}
return n;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];
int deepmax=(n-1)/2;
for(int i=1;i<=deepmax;i++)
{
if(i==1) mp[a[1]]=1;
else
{
int l=powint(i-1),r=powint(i)-1;
LL t=s[r]-s[l-1];
mp[t]=i;
}
}
auto it=mp.begin();
cout<<it->second<<endl;
return 0;
}
双指针算法
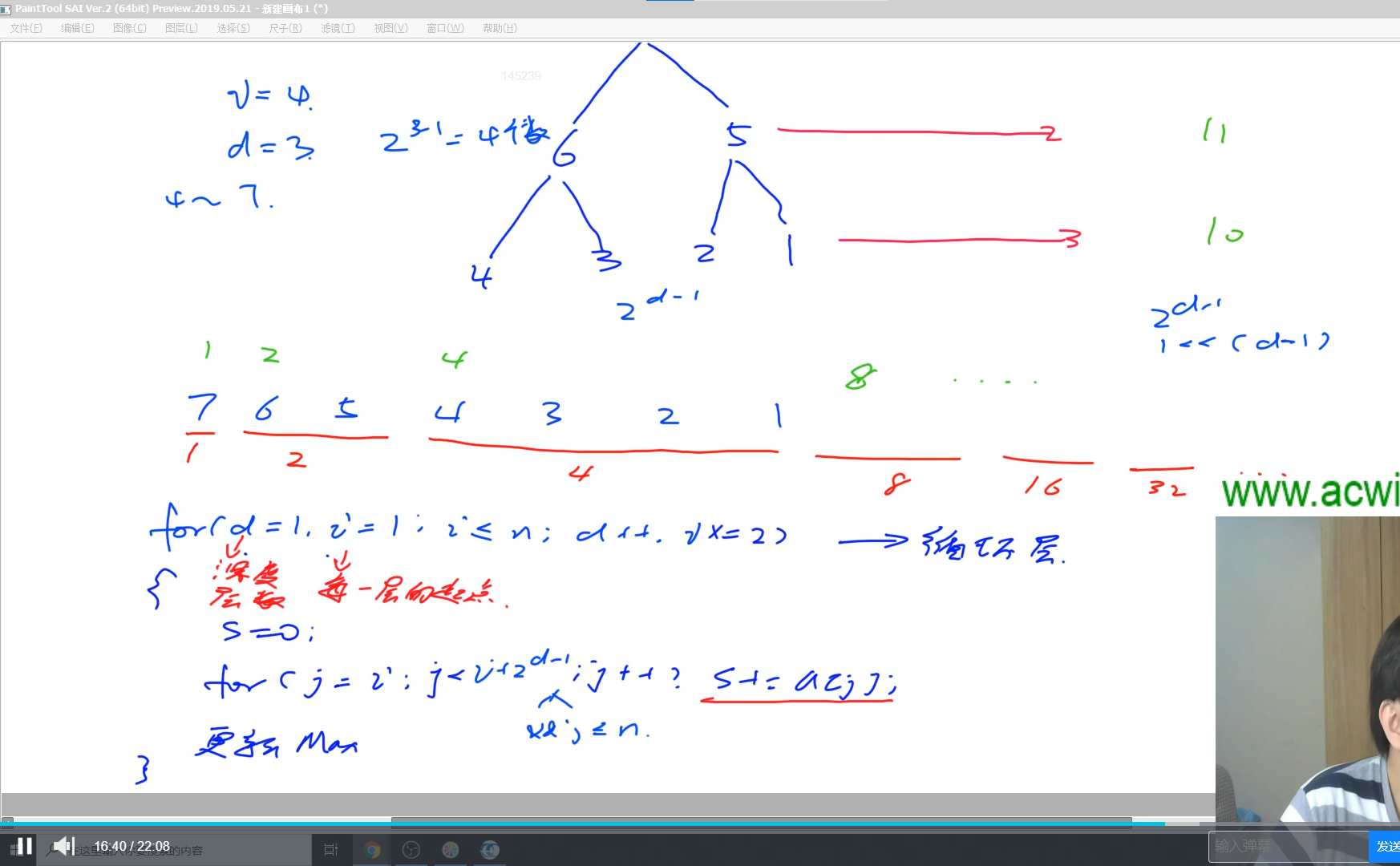
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+10;
int a[N];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
LL maxs=-1e18;
int deep=0;//最大权值的深度
for(int d=1,i=1;i<=n;i*=2,d++)//d是当前深度,i是第几个深度的下标,
{
LL s=0;
for(int j=i;j<i+(1<<d-1)&&j<=n;j++)//计算当前深度的权值
{
s+=a[j];
}
if(s>maxs)//更新答案
{
maxs=s;
deep=d;
}
}
cout<<deep<<endl;
return 0;
}
bfs

void BFS()
{
队列初始化;
初始结点入队;
while (队列非空)
{
队头元素出队,赋给current;
while (current 还可以扩展)
{
由结点current扩展出新结点new;
if (new 重复于已有的结点状态) continue;
new结点入队;
if (new结点是目标状态)
{
置flag= true; break;
}
}
}
}
迷宫问题集合
题目链接: https://vjudge.csgrandeur.cn/problem/%E8%AE%A1%E8%92%9C%E5%AE%A2-T1596
#include<bits/stdc++.h>
using namespace std;
const int N=110;
typedef pair<int,int> PII;
int n,m,sx1,sy1,sx,sy;
int dist[N][N];
char g[N][N];
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
int bfs()
{
memset(dist,-1,sizeof(dist));
queue<PII> q;
dist[sx][sy]=0;
q.push({sx,sy});
while(q.size())
{
PII t=q.front();
q.pop();
int d=dist[t.first][t.second];
for(int i=0;i<4;i++)
{
int x=t.first+dx[i],y=t.second+dy[i];
if(x>=0&&x<n&&y>=0&&y<m&&g[x][y]!='*'&&dist[x][y]==-1)
{
dist[x][y]=d+1;
q.push({x,y});
}
}
}
return dist[sx1][sy1];
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cin>>g[i][j];
if(g[i][j]=='S')
{
sx=i;
sy=j;
}
if(g[i][j]=='T')
{
sx1=i;
sy1=j;
}
}
}
cout<<bfs()<<endl;
return 0;
}
https://vjudge.csgrandeur.cn/problem/%E8%AE%A1%E8%92%9C%E5%AE%A2-T1597
#include<bits/stdc++.h>
using namespace std;
const int N=1000+10,M=1;
typedef pair<int,int> PII;
typedef long long LL;
typedef unsigned long long ULL;
char g[N][N];
int d[N][N];
int n,m,dx,dy,x,y,x2,y2;
int xx[4]={1,0,-1,0},yy[4]={0,1,0,-1};
int bfs()
{
if(x==0||x==n-1||y==0||y==m-1)
return 0;
queue<PII> q;
memset(d,-1,sizeof d);
d[x][y]=0;
q.push({x,y});
while(q.size())
{
PII t=q.front();
q.pop();
for(int i=0;i<4;i++)
{
dx=t.first+xx[i];
dy=t.second+yy[i];
if(dx>=0&&dy>=0&&dx<n&&dy<m&&g[dx][dy]=='.'&&d[dx][dy]==-1)
{
d[dx][dy]=d[t.first][t.second]+1;
q.push({dx,dy});
}
if(g[dx][dy]=='.'&&(dx==n-1||dx==0||dy==m-1||dy==0))
return d[dx][dy];
}
}
return -1;
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
scanf("%s",g[i]);
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
if(g[i][j]=='@')
{
x=i;
y=j;
}
}
}
cout<<bfs()<<endl;
return 0;
}
1113. 红与黑
https://www.acwing.com/problem/content/1115/
bfs求连通子图数
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N=100;
int n,m,sum,sx,sy;
char g[N][N];
bool st[N][N];
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
int bfs()
{
memset(st,false,sizeof(st));
st[sx][sy]=true;
sum=1;
queue<PII> q;
q.push({sx,sy});
while(q.size())
{
auto t=q.front();
q.pop();
for(int i=0;i<4;i++)
{
int x=t.first+dx[i],y=t.second+dy[i];
if(x>=0&&x<n&&y>=0&&y<m&&st[x][y]==false&&g[x][y]!='#')
{
st[x][y]=true;
sum++;
q.push({x,y});
}
}
}
return sum;
}
int main()
{
while(cin>>m>>n)
{
if(n==0&&m==0) break;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cin>>g[i][j];
if(g[i][j]=='@')
{
sx=i;
sy=j;
}
}
}
sum=0;
int t=bfs();
cout<<t<<endl;
}
return 0;
}
1096. 地牢大师
题目链接: https://www.acwing.com/problem/content/1098/
三维迷宫 之前写过
#include<bits/stdc++.h>
using namespace std;
const int N=110;
typedef pair<int,int> PII;
typedef pair<int,PII> PIP;
char g[N][N][N];
int dist[N][N][N];
int n,m,k,res,sx,sy,sz,sx1,sy1,sz1;
int dx[6]={1,-1,0,0,0,0};
int dy[6]={0,0,1,-1,0,0};
int dz[6]={0,0,0,0,1,-1};
int bfs(int x,int y,int z)
{
memset(dist,-1,sizeof(dist));
queue<PIP> q;
dist[x][y][z]=0;
q.push({x,{y,z}});
while(q.size())
{
PIP t=q.front();
q.pop();
for(int i=0;i<6;i++)
{
int nx=t.first+dx[i];
int ny=t.second.first+dy[i];
int nz=t.second.second+dz[i];
if(nx>=0&&nx<n&&ny>=0&&ny<m&&nz>=0&&nz<k&&g[nx][ny][nz]!='#'&&dist[nx][ny][nz]==-1)
{
dist[nx][ny][nz]=dist[t.first][t.second.first][t.second.second]+1;
q.push({nx,{ny,nz}});
}
}
}
return dist[sx1][sy1][sz1];
}
int main()
{
while(cin>>n>>m>>k)
{
if(n==0&&m==0&&k==0) break;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
for(int z=0;z<k;z++)
{
cin>>g[i][j][z];
if(g[i][j][z]=='S')
{
sx=i,sy=j,sz=z;
}
if(g[i][j][z]=='E')
{
sx1=i,sy1=j,sz1=z;
}
}
}
}
res=0;
res=bfs(sx,sy,sz);
if(res==-1) printf("Trapped!\n");
else printf("Escaped in %d minute(s).\n",res);
}
return 0;
}
1233. 全球变暖
https://www.acwing.com/problem/content/1235/
解题报告
1.题意没有看懂,不知道怎么样才算一个岛屿,后面发现题目解释的不好,所谓的岛屿就是这样
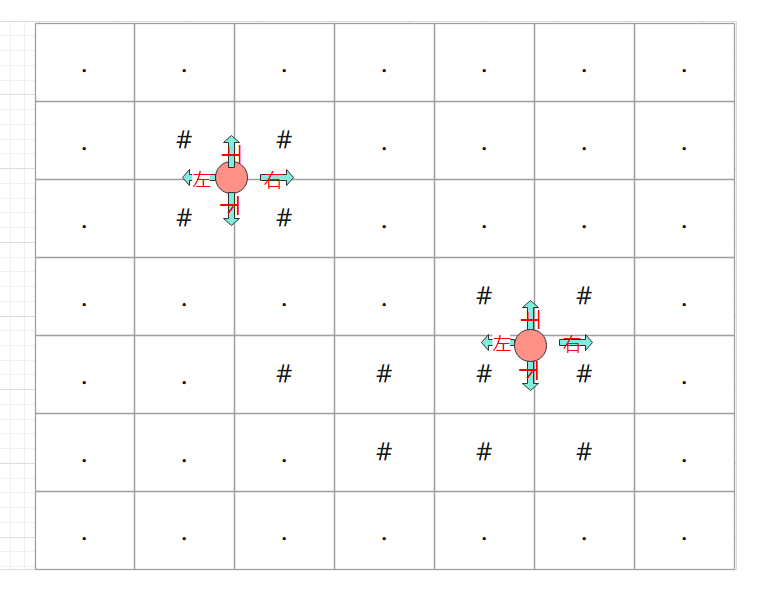
经典的求连通子图问题,当时没有理解的很清楚,担心出现消失了一片陆地后面出现新的岛屿,需要考虑多种情况怎么的,没想出来
y总思路:对于每个连通子图,每次遍历判断其四周是否接触海,接触海表示这边陆地可以被淹没,统计被淹没的陆地和连通子图的节点数,相等表示这个岛屿可以被淹没,cnt记录被淹没岛屿的数量,cnt++即可
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
const int N=1e3+10;
int n,cnt;
char g[N][N];
bool st[N][N];//记录当前节点是否被访问过
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
void bfs(int sx,int sy,int &tot,int &bon)
{
queue<PII> q;
st[sx][sy]=true;
q.push({sx,sy});
while(q.size())
{
PII t=q.front();
q.pop();
tot++;//节点数+1
bool is_bon=false;
for(int i=0;i<4;i++)
{
int x=t.x+dx[i],y=t.y+dy[i];
if(x>=0&&x<n&&y>=0&&y<n&&st[x][y]==false&&g[x][y]=='.')//判断所在的连通子图节点是否邻海
{
is_bon=true;
continue;
}
if(x>=0&&x<n&&y>=0&&y<n&&st[x][y]==false&&g[x][y]=='#')//拓展连通子图
{
q.push({x,y});
st[x][y]=true;
}
}
if(is_bon==true) bon++;//被淹没的陆地数+1
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
cin>>g[i][j];
}
}
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(st[i][j]==false&&g[i][j]=='#')
{
int tot=0,bon=0;
bfs(i,j,tot,bon);
if(tot==bon) cnt++;//连通子图节点数等于被淹没的陆地数,cnt++
}
}
}
cout<<cnt<<endl;
return 0;
}

