$KMP$

记住：跳的永远只是$j$ 永远只在模式串上面跳

模拟$ababac$的$next$求法(最长前缀后缀匹配)

对于每一个$i$，求出匹配的最长前缀和后缀

for(int i = 2, j = 0; i <= m; i++)
{
    while(j && p[i] != p[j+1]) j = next[j];

    if(p[i] == p[j+1]) j++;

    next[i] = j;
}

模拟一下
i  ababac
j  ababac

i=2 j=0
j=0跳过while
p[i]!=p[j+1] next[2]=0

i=3 j=0
p[i]==p[j+1]=a跳出while
j++ j=1
next[3]=1

i=4 j=1
p[i]=p[j+1]=b跳出while
j++ j=2
next[4]=2

j=5 j=2
p[i]=p[j+1]=a跳出while
j++ j=3
next[5]=3

i=6 j=3
p[i]!=p[j+1] j=next[3]=1 i=3的a后面不继续匹配，于是换到了i=1的a继续重新匹配
i=6 j=1
p[i]!=p[j+1] j=next[1]=0
j=0退出while next[6]=0
即最坏情况下找不到和后缀匹配的i,next[j]=0

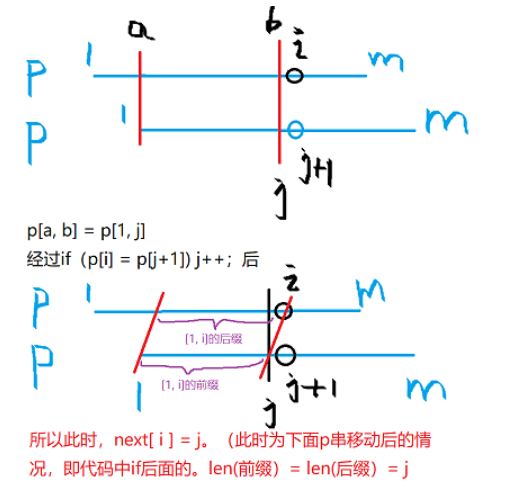
$KMP$核心思想，在$s[i]$和$p[j+1]$不匹配的时候，去找$p$中从$j$往前的后缀 和 从$1$往$j$的前缀 的最长值
再将$j$换到这个前缀的结尾 重新开始匹配操作(这样就可以省去对从$1$到这个前缀结尾的重新搜索)
最坏的情况下，没有前缀和后缀相等，就得重新从$p$串开头搜索

$[1]$ 为什么要用$j+1$?

因为$next$的作用就是在前$j$个已经匹配的条件下，在第$j+1$个元素和第$i$个元素相等时才停下来(如果没有相等的就$j=0$重新从头开始)

$[2]$ 为什么求公共子串的时候$j=2$，查找的时候$j=1$?

因为$ne[1]$没有公共子串，且$ne[1]=0$要用做退出$while$循环的标志

#include<iostream>
using namespace std;
const int M = 1e5+10, N = 1e6+10;
char p[M], s[N];
int ne[M];
int main(){
    int n, m;
    cin >> n >> p + 1 >> m >> s + 1; 
    //因为长度为1的串没有最长相同子序列，所以跳过i=1
    for(int i = 2, j = 0; i <= n; i++){
        //给当前状态下的i尽量通过j=next[j]来找到一个匹配的前缀
        //实在找不到的话，j最终=0，
        while(j && p[i] != p[j+1]) j = ne[j];
        //j替换到下一个位置
        if(p[i] == p[j + 1]) j++;
        //更新ne[i]
        ne[i] = j;
    }
    for(int i = 1, j = 0; i <= m; i++){
        while(j && s[i] != p[j + 1]) j = ne[j];
        if(s[i] == p[j + 1]) j++;
        if(j == n){
            printf("%d ", i - n); //j=n之后, p[j + 1] ='/n'，没有与其相等的s[i],j=ne[j]继续搜索
            j = ne[j];
        }
    }
    return 0;
}