容斥原理
for(int i = 1; i < n; i++){
int m = p[i].size(); 质因子的个数
ll tmp = 0;
for(int j = 1; j < 1 << m; j++){
ll ret = -1;
for(int k = 0; k < m; k++)
if(j & (1 << k)) ret *= -p[i][k]; 选出的质因子的乘机
ll now = (n - i) / ret;
tmp += now;
}
ans += (n - i - tmp) * f[i];
}
质数筛
void init(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
约数个数和约数之和
如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数: (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和: (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)
欧几里得算法 (辗转相除法)
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
欧几里得算法 (辗转相减法) 时间复杂度最坏会退化到O(n) 但是当用倍数情况时需用此算法
int gcd_sub(int a, int b)
{
if(a < b) swap(a, b);
if(b == 1) return a;
return gcd_sub(b, a / b);
}
扩展欧几里得算法
// 求x, y,使得ax + by = gcd(a, b)
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1; y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= (a/b) * x;
return d;
}
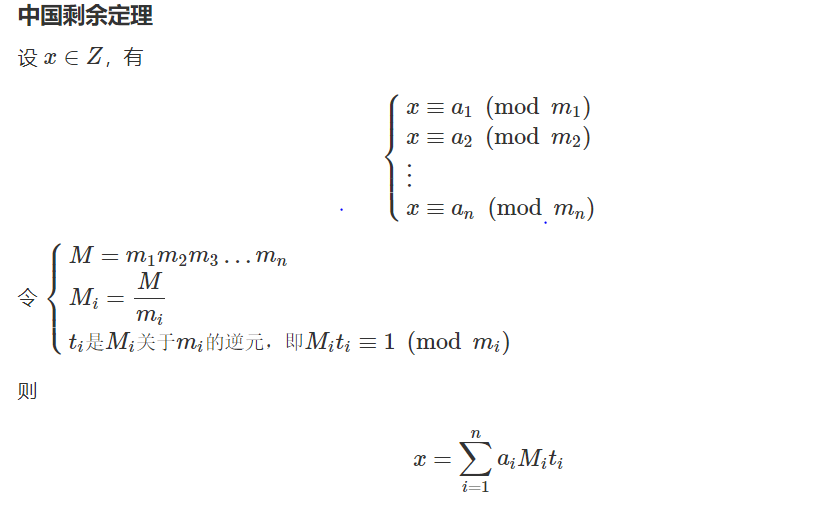
筛法求欧拉函数

void get_eulers(int n)
{
euler[1] = 1;
for (int i = 2; i <= n; i ++ )
{
if (!st[i])
{
primes[cnt ++ ] = i;
euler[i] = i - 1;
}
for (int j = 0; primes[j] <= n / i; j ++ )
{
int t = primes[j] * i;
st[t] = true;
if (i % primes[j] == 0)
{
euler[t] = euler[i] * primes[j];
break;
}
euler[t] = euler[i] * (primes[j] - 1);
}
}
}
快速幂
int qmi(int m, int k, int p)
{
int res = 1 % p, t = m;
while (k)
{
if (k&1) res = res * t % p;
t = t * t % p;
k >>= 1;
}
return res;
}
光速幂
原理 : a ^ b mod p <==> a ^ (k * s + t) mod p
所以预处理a^0, a^1, a^2 … a^s; a^s, a^2s, a^3s … a^[p/s];
即可查表得出答案
int phi(int x){
int res=x;
for(int i=2;i*i<=x;i++){
if(x%i==0)res=res/i*(i-1);
while(x%i==0)x/=i;
}
if(x>1)res=res/x*(x-1);
return res;
}
int Qpow(int n){
n%=phi(p);
return 1ll*poww[n%bl][0]*poww[n/bl][1]%p;
}
龟速乘
LL qadd(LL a, LL b, LL p)
{
LL res = 0;
while (b)
{
if (b & 1) res = (res + a) % p;
a = (a + a) % p;
b >>= 1;
}
return res;
}
高斯消元
int gauss()
{
int c, r;
for (c = 0, r = 0; c < n; c ++ )
{
int t = r;
for (int i = r; i < n; i ++ ) // 找到绝对值最大的行
if (fabs(a[i][c]) > fabs(a[t][c]))
t = i;
if (fabs(a[t][c]) < eps) continue;
for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]); // 将绝对值最大的行换到最顶端
for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c]; // 将当前行的首位变成1
for (int i = r + 1; i < n; i ++ ) // 用当前行将下面所有的列消成0
if (fabs(a[i][c]) > eps)
for (int j = n; j >= c; j -- )
a[i][j] -= a[r][j] * a[i][c];
r ++ ;
}
if (r < n)
{
for (int i = r; i < n; i ++ )
if (fabs(a[i][n]) > eps)
return 2; // 无解
return 1; // 有无穷多组解
}
for (int i = n - 1; i >= 0; i -- )
for (int j = i + 1; j < n; j ++ )
a[i][n] -= a[i][j] * a[j][n];
return 0; // 有唯一解
}
组合数
递归法求解
for (int i = 0; i < N; i ++ )
for (int j = 0; j <= i; j ++ )
if (!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
预处理逆元求解
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
Lucas定理求解
若p是质数,则对于任意整数 1 <= m <= n,有:
C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)
int C(int a, int b, int p) // 通过定理求组合数C(a, b)
{
if (a < b) return 0;
LL x = 1, y = 1; // x是分子,y是分母
for (int i = a, j = 1; j <= b; i --, j ++ )
{
x = (LL)x * i % p;
y = (LL) y * j % p;
}
return x * (LL)qmi(y, p - 2, p) % p;
}
int lucas(LL a, LL b, int p)
{
if (a < p && b < p) return C(a, b, p);
return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
分解质因数高精度求解
当我们需要求出组合数的真实值,而非对某个数的余数时,分解质因数的方式比较好用:
1. 筛法求出范围内的所有质数
2. 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + ...
3. 用高精度乘法将所有质因子相乘
int primes[N], cnt; // 存储所有质数
int sum[N]; // 存储每个质数的次数
bool st[N]; // 存储每个数是否已被筛掉
void get_primes(int n) // 线性筛法求素数
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
int get(int n, int p) // 求n!中的次数
{
int res = 0;
while (n)
{
res += n / p;
n /= p;
}
return res;
}
vector<int> mul(vector<int> a, int b) // 高精度乘低精度模板
{
vector<int> c;
int t = 0;
for (int i = 0; i < a.size(); i ++ )
{
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (t)
{
c.push_back(t % 10);
t /= 10;
}
return c;
}
get_primes(a); // 预处理范围内的所有质数
for (int i = 0; i < cnt; i ++ ) // 求每个质因数的次数
{
int p = primes[i];
sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i ++ ) // 用高精度乘法将所有质因子相乘
for (int j = 0; j < sum[i]; j ++ )
res = mul(res, primes[i]);
卡特兰数

类型:
1、括号匹配
2、不相交的弦
3、进出栈
4、不出现“312”的全排列
5、二叉树的构成问题
6、凸边形的三角划分
7、阶梯的矩阵划分
矩阵乘法优化时间复杂度
void mul(int c[][N], int a[][N], int b[][N])
{
int temp[N][N] = {0};
for(int i = 0; i < N; i++)
for(int j = 0; j < N; j++)
for(int k = 0; k < N; k++)
temp[i][j] = (temp[i][j] + (ll)a[i][k] * b[k][j]) % m;
memcpy(c, temp, sizeof temp);
}
斐波那契数列的一些性质
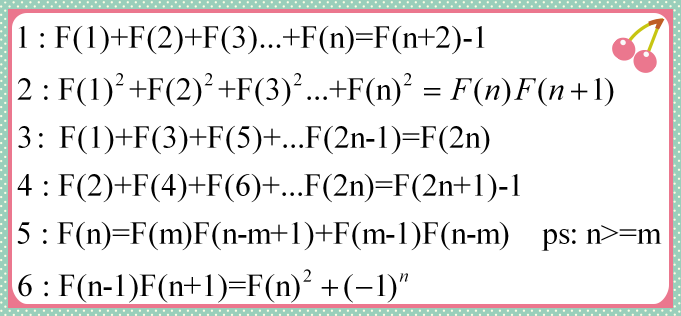
线性基
求异或最大值/最小值/第k值
for (int i = 62; i >= 0; i -- )
{
for (int j = k; j < n; j ++ )
if (a[j] >> i & 1)
{
swap(a[j], a[k]);
break;
}
if (!(a[k] >> i & 1)) continue;
for (int j = 0; j < n; j ++ )
if (j != k && (a[j] >> i & 1))
a[j] ^= a[k];
k ++ ;
if (k == n) break;
}
sg函数
当分离出多个状态时 注意sg的异或
int sg(int x)
{
if(f[x] != -1) return f[x];
set<int> S;
for(int i = 0; i < m; i++)
{
int sum = s[i];
if(x >= sum) S.insert(sg(x - sum));
}
for(int i = 0; ; i++)
if(!S.count(i)) return f[x] = i;
}

