最长上升子序列

最长上升子序列问题是在一个无序的给定序列中找到一个尽可能长的由低到高排列的子序列，
这种子序列不一定是连续的或者唯一的。
因为所求为子序列，很容易想到一种线性动态规划。 对于求最长上升子序列，上升我们肯定需要知道当前阶段最后一个元素为多少，
最长我们还要知道当前我们的序列有多长。

模型1—>最长上升子序列模型

时间复杂度:O(n^2)
相关例题- 1017. 怪盗基德的滑翔翼
思路分析(图解):

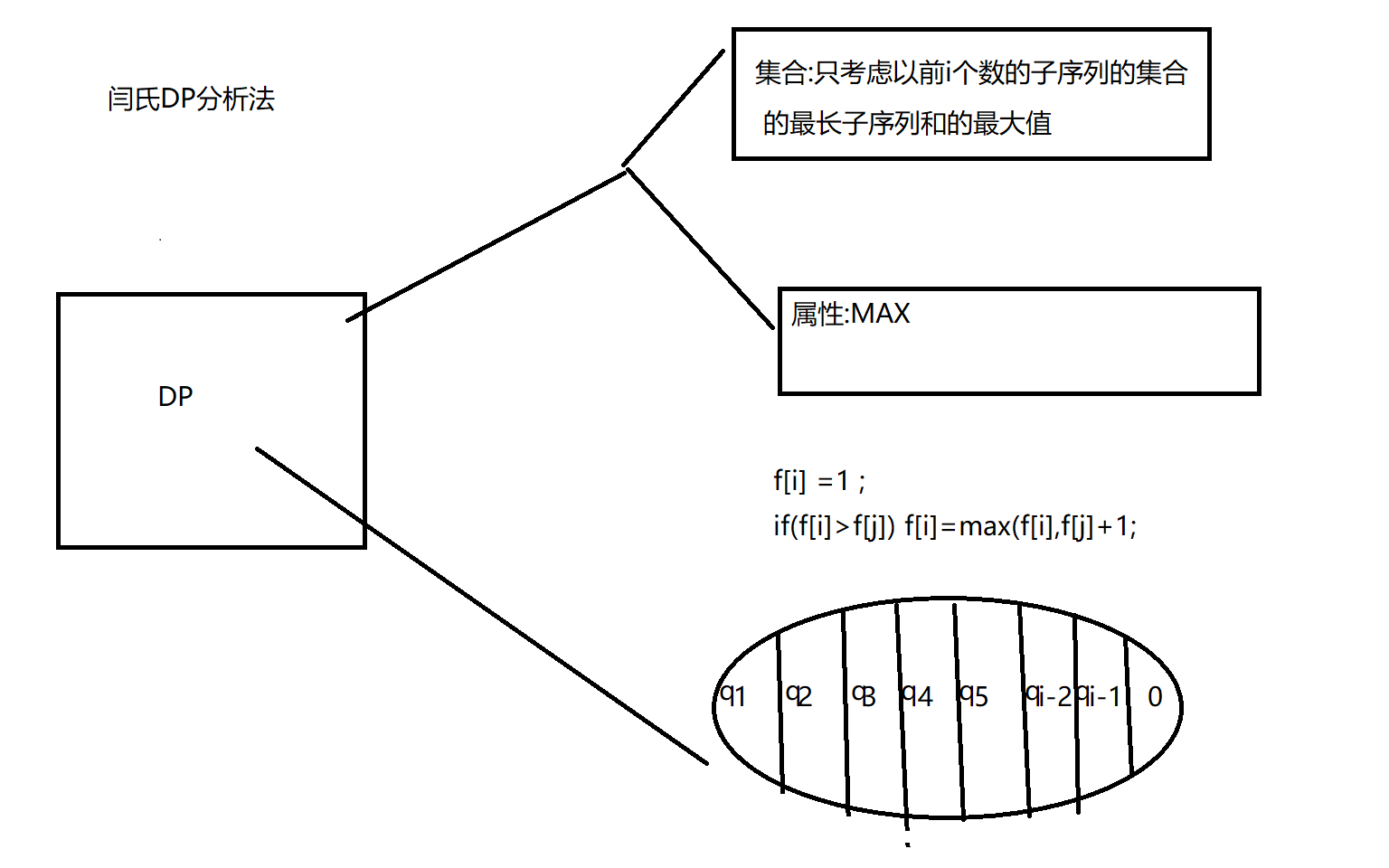
<–—关键信息描述—>
初始时，怪盗基德可以在任何一幢建筑的顶端。 ---->子序列的起点不确定
他希望尽可能多地经过不同建筑的顶部，这样可以减缓下降时的冲击力，减少受伤的可能性。—>子序列的终点不确定
==>综上:标准的LCS模板
代码表示:

#include<bits/stdc++.h>
using namespace std;
const int N=110,M=10010;
int s[N];
int q[N];
//二维
int t;
int main(){
  cin>>t;
  while(t--){
    int n;
    cin>>n;
    memset(q,0,sizeof q);
    memset(s,0, sizeof s);
    for(int i=1;i<=n;i++)cin>>q[i];
    int max_num=-1;
    //从逻辑的角度---->在确定s[i]之前s[j]已经被确定下来
    for(int i=1;i<=n;i++){
         s[i]=1;
        for(int j=1;j<i;j++){
          if(q[j]>q[i])s[i]=max(s[i],s[j]+1);
          max_ans=max(max_ans,s[i);
        }
    }
    memset(s,0, sizeof s);

    for(int i=n;i>=1;i--){
         s[i]=1;
        for(int j=n;j>i;j--){
          if(q[j]>q[i])s[i]=max(s[i],s[j]+1);
        }
    }
    for(int i=1;i<=n;i++){
      max_num=max(max_num,s[i]);
    }
    memset(s,0, sizeof s);
    for(int i=n;i>=1;i--){
         s[i]=1;
        for(int j=n;j>i;j--){
          if(q[j]>q[i])s[i]=max(s[i],s[j]+1);
          max_ans=max(max_ans,s[i);
        }
    }
    //重置不要忘记
    memset(s,0, sizeof s);
    for(int i=n;i>=1;i--){
         s[i]=1;
        for(int j=n;j>i;j--){
          if(q[j]>q[i])s[i]=max(s[i],s[j]+1);
        }
    }
    for(int i=1;i<=n;i++){
      max_num=max(max_num,s[i]);
    }
    cout<<max_num<<endl;
  }
  return 0;
}

模型 最长上升子序列模型的优化版本

时间复杂度:O(nlogn)
优化对应代码如下:

    for(int i=1;i<=n;i++){
         s[i]=1;
        for(int j=1;j<i;j++){
          if(q[j]>q[i])s[i]=max(s[i],s[j]+1);
          max_ans=max(max_ans,s[i);
        }
    }

1.首先：时间复杂度在内层循环的过程中造成了重复记录的现象
(思路O(n)=======>O(logn))
logn=>二分算法==>二段性(单调性)
贪心：假设长度为i(1<=i && i<=n)的上升字串的结尾数字的最小值具备单调递增的特性
//图片
//特别注意二分的写法问题

相关例题- 1014. 登山
思路分析(图解):
<–—关键信息描述—>
就是不连续浏览海拔相同的两个景点，并且一旦开始下山，就不再向上走了
=>综上标准LCS模板(注意:方向问题)
代码描述

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int n,ans;
int s1[N],s2[N];
int q[N];
int main(){
  cin>>n;
  for(int i=1;i<=n;i++)cin>>q[i];
  for(int i=1;i<=n;i++){
      s1[i]=1;
      for(int j=1;j<i;j++){
        if(q[j]<q[i])s1[i]=max(s1[i],s1[j]+1);
      }
  }
  for(int i=n;i>=1;i--){
      s2[i]=1;
      for(int j=n;j>i;j--){
        if(q[j]<q[i])s2[i]=max(s2[i],s2[j]+1);
      }
  }
  //错误写法如下:
  /*
  s2[i](!一定等于)s2[i-1]+1;
  for(int i=1;i<n;i++){
    ans=max(ans,s1[i]+s2[i+1]);
    ans=max(ans,s1[i-1]+s2[i]);
  } 
  */
  for(int i=1;i<=n;i++){
    ans=max(ans,s1[i]+s2[i]-1);
  }
  cout<<ans;
  return 0;
}

相关例题- 482. 合唱队形
思路分析(图解):
<–—关键信息描述—>
代码表示:

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n,ans=1e9+10;
int s1[N],s2[N];
int q[N];
int main(){
  cin>>n;
  for(int i=1;i<=n;i++)cin>>q[i];
  for(int i=1;i<=n;i++){
      s1[i]=1;
      for(int j=1;j<i;j++){
        if(q[j]<q[i])s1[i]=max(s1[i],s1[j]+1);
      }
  }
  for(int i=n;i>=1;i--){
      s2[i]=1;
      for(int j=n;j>i;j--){
        if(q[j]<q[i])s2[i]=max(s2[i],s2[j]+1);
      }
  }
  //思路与上一题相同加了一个步骤而已
  for(int i=1;i<=n;i++){
    ans=min(ans,n-(s1[i]+s2[i]-1));
  } 
  cout<<ans;
  return 0;
}

相关例题- 1016. 最大上升子序列和
思路分析(图解):
<–—关键信息描述—>
即求得以每个点为转折点(并且左右均为上升子序列的最多个数的子序列和)
代码表示:

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int s[N];
int q[N];
int n;
int main(){
  cin>>n;
  for(int i=1;i<=n;i++)cin>>q[i];
  for(int i=1;i<=n;i++){
     s[i]=q[i];
    for(int j=1;j<i;j++){
      if(q[j]<q[i])s[i]=max(s[i],s[j]+q[i]);
    }
  }
  int ans=0;
  for(int i=1;i<=n;i++){
    ans=max(ans,s[i]);
  }
  cout<<ans;
  return 0;
}

模型2—>最长公共子序列模型

相关例题- 897. 最长公共子序列
思路分析(图解):

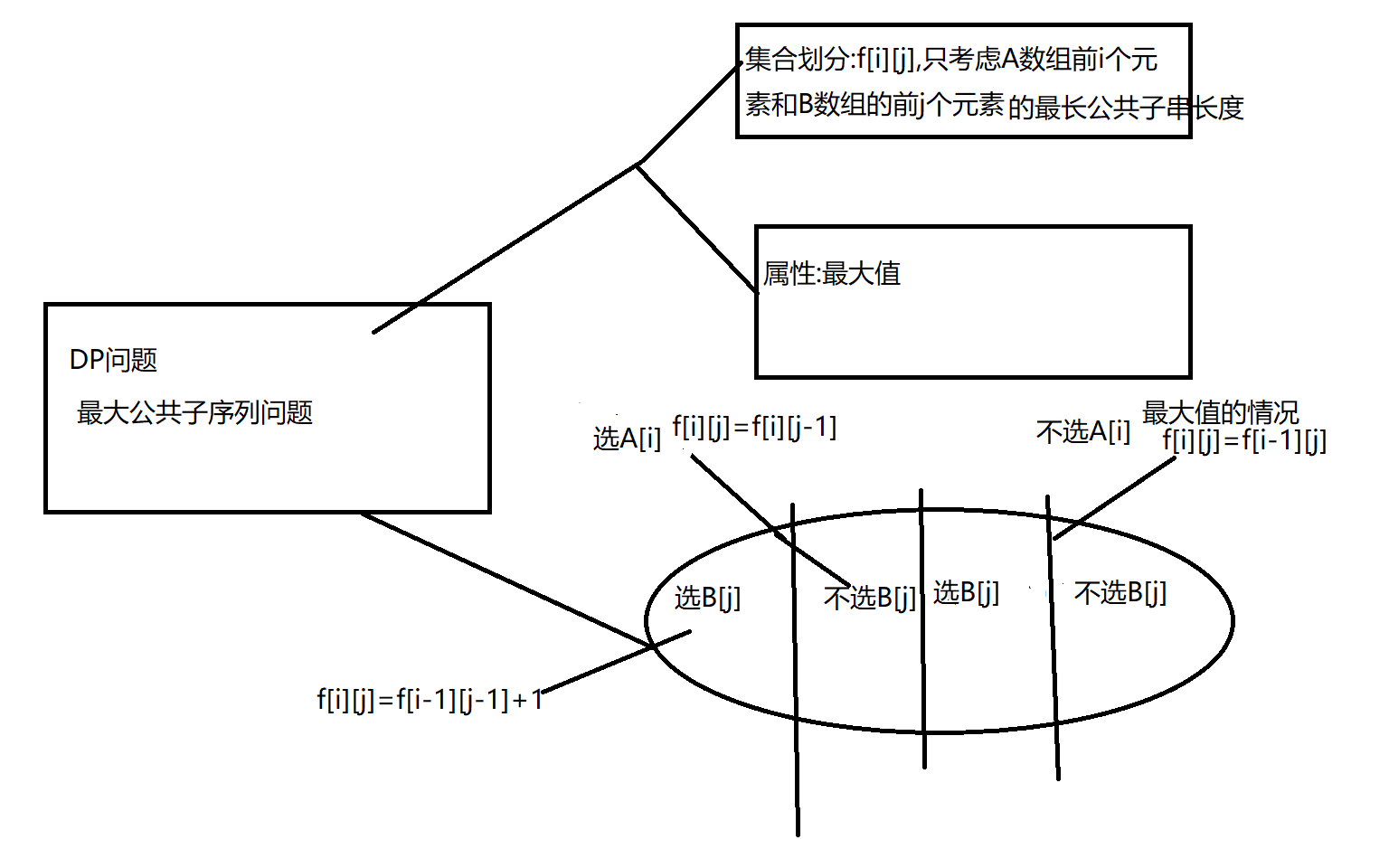
<–—关键信息描述—>
代码展示

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int f[N][N];
int n,m;
char a[N],b[N];
int main (){
    cin>> n >> m >> a + 1>> b + 1;
    for(int i=1;i<=n;i++){
      for(int j=1;j<=m;j++){
        f[i][j]=max(f[i][j-1],f[i-1][j]);
        if(a[i]==b[j]){
          f[i][j]=max(f[i][j],f[i-1][j-1]+1);
        }
      }
    }
    cout<<f[n][m]<<endl;
    return 0;
}

//DP数组的初始化非常重要

模型3—>最长上升公共子序列模型

相关例题- 272. 最长公共上升子序列
思路分析(图解):

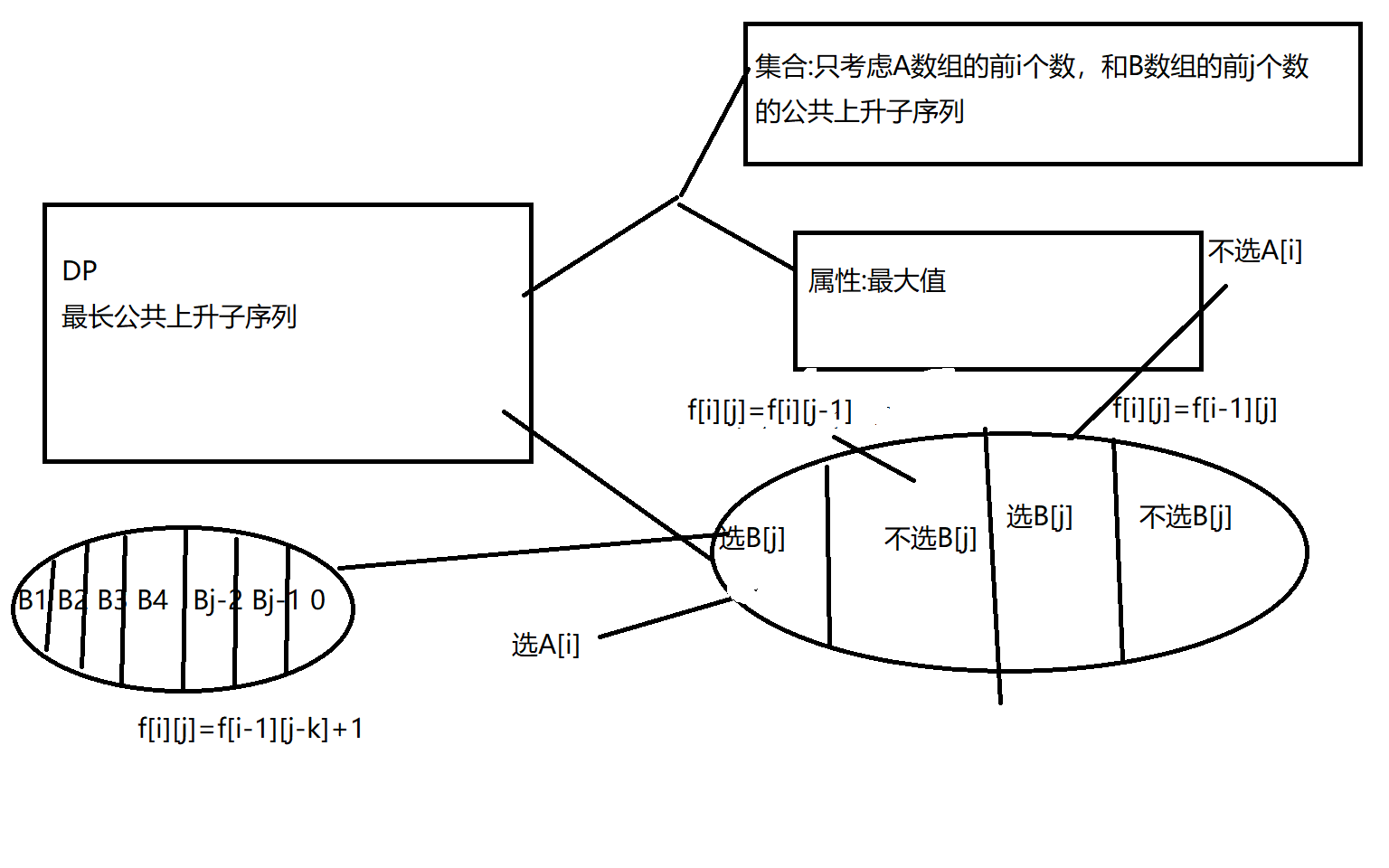
<–—关键信息描述—>

#include<bits/stdc++.h>
using namespace std;
const int N = 3010;
int a[N],b[N];
int f[N][N];
int n;
int main(){
  cin>>n;
  for(int i=1;i<=n;i++)cin>>a[i];
  for(int i=1;i<=n;i++)cin>>b[i];
  for(int i=1;i<=n;i++){
    for(int j=1;j<=n;j++){
        //。。。。。。。有问题
      //在处理f[i][j]时，答案已经包含的是f[i-1][j]和f[i][j-1]的
      f[i][j]=max(f[i][j-1],f[i-1][j]);
      if(a[i]==b[j]){
        f[i][j]=max(f[i][j],1);
        for(int k=1;k<j;k++){
          if(b[k]<b[j])f[i][j]=max(f[i][j],f[i-1][k]+1);
        }
      }
    }
  }
    int ans = 0;
    for(int i = 1; i <= n; i++) ans = max(ans, f[n][i]);
    cout << ans << endl;
    return 0; 
}