一维前缀和

前缀和本质上是一个公式及其应用。

$$ 对于一列数: a_1, a_2, a_3…, a_n, 定义下标从1开始， 令S_0 = 0, S_k = 0 + a_1 + a_2 + … + a_k。S_k就是一个前缀和。 $$

公式的应用

$$ 我们可以在O(1)时间内求出任意区间元素的和。[L, R]区间内元素的和为：\\ S_{R} - S_{L - 1} = a_{L} + a_{L + 1} + … + a_{R - 1} + a_{R}。 $$

预处理

$$ 预处理复杂度和输入复杂度一样，均为O(n), S_r = S_{r - 1} + a_r; $$

二维前缀和

二维前缀和是基于矩阵的前缀和，本质上和一维前缀和区别不大。

$$ 对于一个A* B的矩阵M，S_{ij}定义为以(i, j)为下标的元素的左上角的小矩形里的全部元素的和。 $$

公式的应用

$$ 同样地，我们可以在O(1)时间内求出一个矩形范围内的元素的和, 例如求粉色区域的元素的和:\\ S_{\theta} = S_{xy} - S_{xj - 1} - S_{i - 1y} + S_{i-1j-1} $$

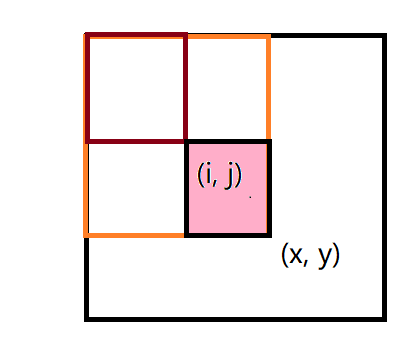
预处理

$$ 预处理复杂度和读取输入复杂度一样。 S_{xy} = S_{x-1y}+S_{xy-1}+M_{xy}-S_{x-1y-1}; $$

差分

差分是前缀和的逆运算

$$ 对于数列\{a_n\}, 构造数列\{b_n\}, 使得\forall k\in N^+, a_k = S_k, S_k = b_1 + b_2+…+b_k. 即:\\ b_1 = a_1, b_2 = a_2 - a_1, b_3 = a_3-a_2… 此时，称b_n是a_n的差分，a_n是b_n的前缀和。 $$

公式的应用

$$ 我们可以做到在O(1)时间内对\{a_n\}中[L, R]区间的数字都加上c，注意，这种+c的操作是隐式的。当这种+c的操作需求很多时，效率上即有优势。\\ 具体做法是: 当要求对\{a_n\}的[L, R]区间内的每个元素加c时，只需对a_n的差分数组b_n的元素b_l+c，此时若对\{b_n\}数列求前缀和S_k(k\ge r)，\\每个前缀和S_k(也即a_k)实际上都加上了c，此时我们只需要对b_{r+1}-c，保证在区间范围之后的元素没有受影响即可。当我们需要取\{a_n\}中某个元素\\时，只需对\{b_n\}求前缀和。由于\{b_n\}暗含了\{a_n\}，有时我们可以不存储\{a_n\}。 $$

差分的构造方式

$$ 差分有两种构造方式: \\ (1) 定义构造法， b_1 = a_1， b_2 = a_2 - a_1… \\ (2) 增c构造法， b_1 = Range([1，1])+c ==> b_1+c, b_2-c.\\ 二者本质上没有区别。 $$

• 注意

对每个元素隐式+c的操作需要的时间复杂度是O(1)，但取元素时的时间复杂度是O(n)。这使得差分使用时要尽量少取元素，或者在增c操作全部结束后，大量查询(此时可以一次性求出全部元素)。

二维差分

$$ 在二维差分中，同理，我们对二维矩阵M，可以构造它的差分矩阵N，使得对于M中的元素M_{ij}， 它是差分矩阵N中(i,j)元素左上角全部元素的和.\\ $$

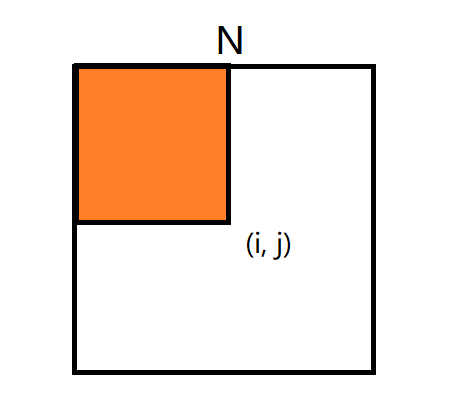
$$ 即: M_{ij}是上述橙色部分的全部元素的和。 $$

应用

$$ 给某个子矩阵内的元素全部加上c(隐式)。具体操作是对差分子矩阵左上角的元素N_{x1y1}+c，此时该元素右下角全部元素都会受到影响(包含此元素)，\\为了消除过多的影响，我们需要对子矩阵之外的元素作补偿。也就是N_{x_2 + 1 y_1} - c， N_{x_1 y_2 + 1} - c，N_{x_2 + 1 y_2 + 1} + c. 如果需要求M中的\\某个元素，只需对N中的元素求前缀和即可，求前缀和的方式参见二维前缀和。 $$

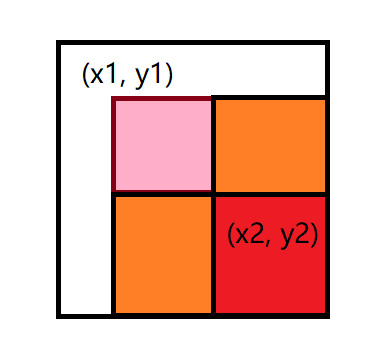
二维差分的构造方式

$$ 相当于每次对区间(坐标对), [(1， 1), (1， 1)]，[(1， 2), (1， 2)]…[(n，m), (n，m)]进行全部+c。隐式构造。 $$

• 注意

同样地，二维差分中，+c操作的时间复杂度是O(1)的，但是单次查询是O(nm)的，涉及到求前缀和。