次小生成树

定义：给定一个带权的图，把图的所有生成树按照权值从小到大排序，权值和第二小的称为次小生成树

求法

① 非严格次小生成树(可以取等)

先求最小生成树，在枚举删去最小生成树中的边求解。$O(mlogm+nm)$

证明：

假设存在存在一个图(如下图)，它的最小生成树和次小生成树至少差两条边。

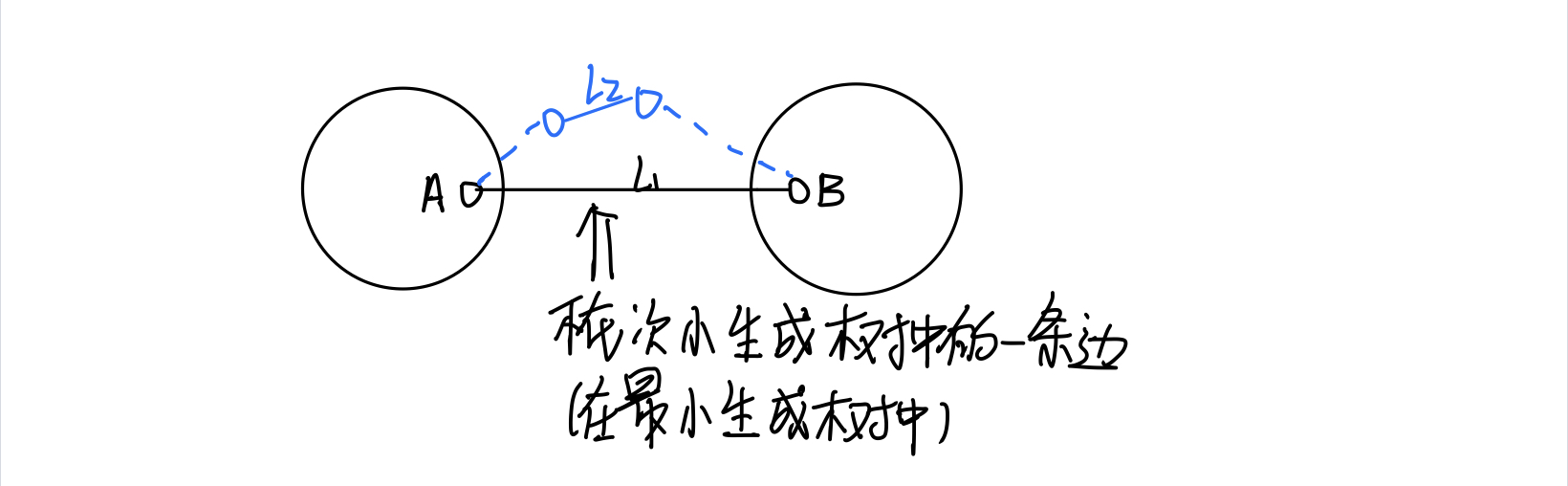
因为不通过$l1$将这两个端点连接，那么就要通过其他路径将这两个点连接。因为$l1$为连接$A$,$B$的的最先枚举的边，所以$l2$上面的边的权值都是大于等于$l1$权值的($Kruskal$过程)，那么就可以将$l2$删去，加上$l1$，次小生成树的总权值一定不会更大，这样就可以减少一条不同边。所以只要次小生成树和最小生成树之间不同的边超过两条，那么就可以采用上面这种操作，将不同的边换成一条最小生成树中的边，最后换到只剩一条边不同。
故：通过枚举删除最小生成树中的边可以不漏的枚举出所有次小生成树，及维护次小生成树的权值。

② 严格次小生成树(严格小于)

先求最小生成树，然后依次枚举非树边，然后将该边加入树中，同时从树中去掉一条边，使得最终的图仍是一棵树，则一定可以求出次小生成树。
即：设T为图G的一棵生成树，对于非树边$a$和树边$b$，插入$a$，将删除$b$的操作记为$(+a,-b)$
如果$T+a-b$之后，仍然是一棵生成树，称$(+a,-b)$是$T$的一个可行变换。称由$T$进行一次可行变换所得到的新的生成树集合为$T$的邻集。
则有定理：次小生成树一定在最小生成树的邻集中
因为是严格小于，所以去掉的$l2$和$l1$权值不能相同，而且每次去掉的$l2$应为最小生成树上$a到b$路径上的最大边权，只有这样次小生成式才能取最小。

证明同非严格次小生成树，严格次小生成树集合也一定对应最小生成树换一条边后的树集合。但是去掉的边应该严格大于$w[l2]$且为路径上最大。

$Example:$

$dfs$求两个点之间的最短距离和次小距离($O(N^2)$)：$Acwing1148$.秘密的奶牛运输
用$LCA$倍增求两个点之间的最短距离和次小距离($O(NMlognN)$)：$Acwing356$.次小生成树