来自图论
最小生成树
Prim 算法和 Kruskal 算法
最小生成树
Prim
通过更新点到集合的最短距离,逐渐构造最小生成树
远看代码好像是dijkstra,实际上这是因为prim算法的原理与其相似。
和dijkstra一样,每次找到距离最近的一个点加入集合,再用这个点去更新其他节点。
这样的操作,会以递进的方式逐渐将所有点到集合的距离变到最小,且无重复的边,则形成一颗最小生成树。
先将一个点作为根节点塞入集合,更新他所连接的点。
然后将一个距离最近的点加入集合,再通过这个点更新遍历其他点。
不断进行此操作,直至遍历所有的结点。
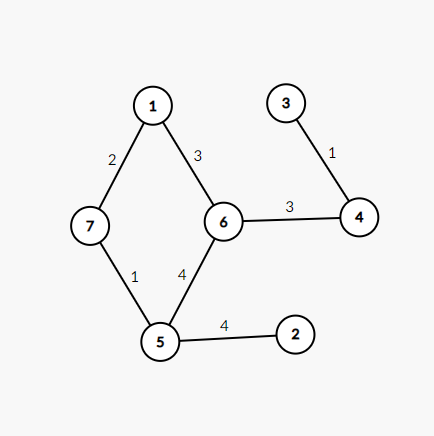
以该图为例,我们进行如下的推导:
集合 集合内边的权值之和 描述
0 1 0 操作前将1放入集合当作根节点
1 1,7 2 将2放入集合
2 1,7,5 3 将3放入集合
3 1,7,5,6 6 将6放入集合
4 1,7,5,6,4 9 将4放入集合
5 1,7,5,6,4,3 10 将3放入集合
6 1,7,5,6,4,3,2 14 将2放入集合
通过程序可以发现,加入集合的顺序正好是1,7,5,6,4,3,2,最小生成树的树边权重之和为14.
完成了的最小生成树
![]
O(N)
AC code
#include<bits/stdc++.h>
using namespace std;
const int N=510,INF=0x3f3f3f3f;
int n,m;
int g[N][N];
int d[N]; bool st[N];
int prim()
{
memset(d,0x3f,sizeof d);
int res=0;
for(int i=0;i<n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
if(!st[j]&&(t==-1||d[t]>d[j]))
t=j;
if(i&&d[t]>=INF/2) return INF;
if(i) res+=d[t];
for(int j=1;j<=n;j++) d[j]=min(d[j],g[t][j]);
st[t]=true;
}
return res;
}
int main()
{
memset(g,0x3f,sizeof g);
cin>>n>>m;
while(m--){
int a,b,c; cin>>a>>b>>c;
g[a][b]=g[b][a]=min(g[a][b],c);
}
int ans=prim();
if(ans>=INF/2) puts("impossible");
else cout<<ans;
return 0;
}
最小生成树的性质
在一个有N个结点的无向图中:
- 它的最小生成树必有N-1边
- 最小生成树的权值之和小于或等于其他生成树
- 若该图不连通,无生成树
通过以上几点可以对一个图做一些基础的最小生成树判断。
题目
Acwing.858 Prim求最小生成树
Acwing.858 代码
Acwing.1140 最短网络
Acwing.1140 代码
Kruscal
贪婪的算法
这个算法以贪心为轴线,展开最小生成树的构造。
和prim算法一样,有一个集合。
将所有边按从小到大排序,然后从小到大遍历每一条边。
在遍历过程中,判断他们是否在同一集合内,如果不在就将他们合并,如果在,则表示这是一条多余的边,已经有更短的边了,所以可以直接舍去。
图例

还是拿上面的图下手。
排好序的边:
5 7
3 4
1 7
1 6
4 6
5 2
5 6
集合 集合内边的权值之和 描述
0 NULL 0
1 5,7 1 +5,7
2 3,4,7,5 2 +3,4
3 3,4,7,5,1 4 + 1
4 1,7,3,4,5,6 7 + 6
5 1,7,3,4,5,6 10 合并两个集合
6 1,7,5,6,4,3,2 14 + 2
完成了的最小生成树
通过上述的推导,发现Kruscal算法可以保证最优解
O(E log E)
AC_code
#include<bits/stdc++.h>
using namespace std;
const int N=200010;
struct edge{
int a,b,w;
}e[N];
bool cmp(const edge a,const edge b){
return a.w<b.w;
}
int n,m;
int f[N]; //并查集
int cnt=1; //记录点数
int find(int x)
{
if(f[x]!=x) f[x]=find(f[x]);
return f[x];
}
int kruscal()
{
int res=0;
for(int i=1;i<=n;i++) f[i]=i; //初始化集合
for(int i=0;i<m;i++)
{
int a=e[i].a,b=e[i].b,w=e[i].w;
a=find(a),b=find(b);
if(a!=b)
{
f[a]=b;
res+=w;
cnt++;
}
}
return res;
}
int main()
{
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b,c; cin>>a>>b>>c;
e[i]={a,b,c};
}
sort(e,e+m,cmp);
int ans=kruscal();
if(cnt<n) puts("impossible");
else cout<<ans;
return 0;
}
题目
Acwing.859 Kruskal算法求最小生成树
Acwing.859 代码
Acwing.1141 局域网
Acwing.1141 代码
Acwing.1142 繁忙的都市
Acwing.1142 代码
制作不易
如果发现学术问题,请私聊我;如果你觉得对你有帮助,就支持一下我。


