背包模型

01背包问题

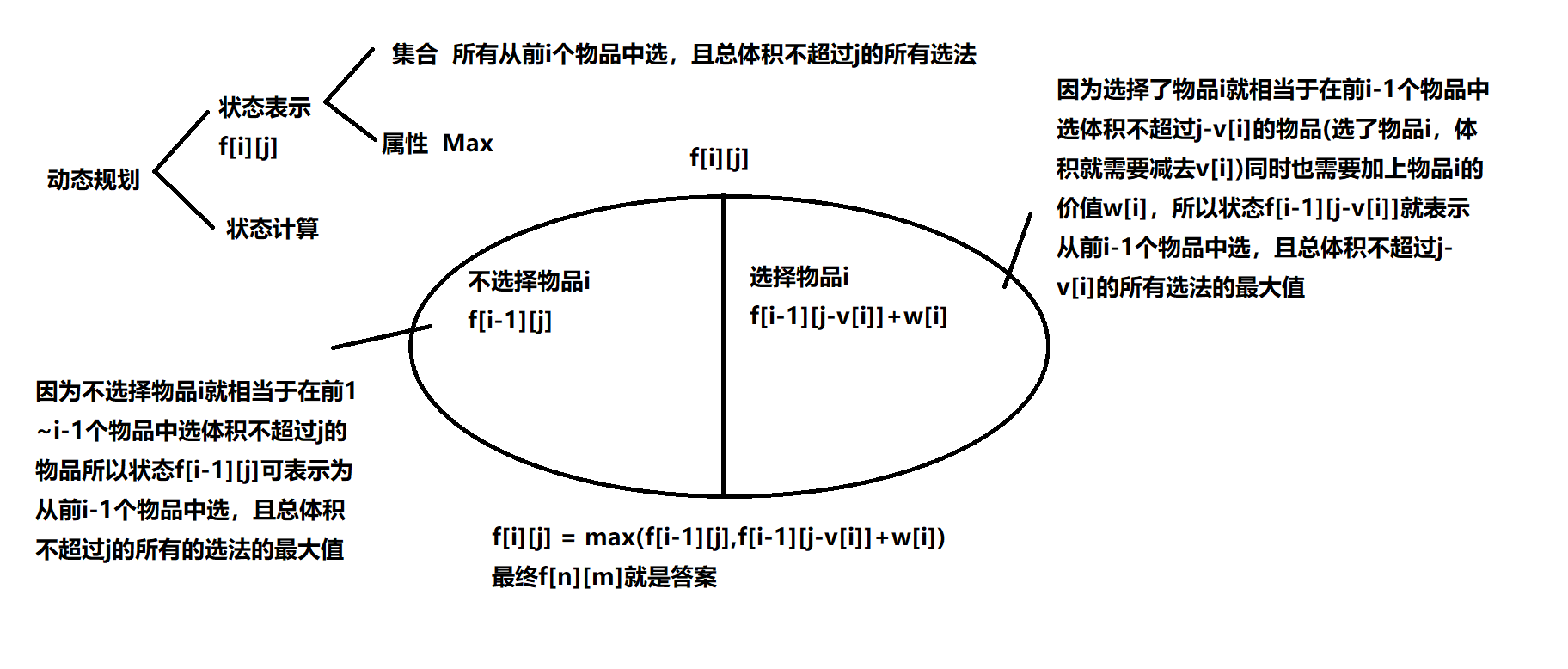
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;

const int N = 1010;

int n, m, f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        int v, w;
        cin >> v >> w;
        for(int j = 0; j <= m; j ++){
            f[i][j] = f[i - 1][j];// 这个如果不赋值，就丢失f[i][j < v[i]]的数据
            if(j >= v)  f[i][j] = max(f[i][j], f[i - 1][j - v] + w);
        }
    }
    cout << f[n][m] << endl;

    return 0;

}

滚动数组优化

从推导公式f[i,j] = max(f[i-1,j], f[i - 1, j - vi] + wi)可以看出，第i阶段的状态只和i-1阶段的状态有关，所以我们可以将f数组的空间由[0~n,0~m]改为[0~1,0~m]，通过变量c来控制每次用到的哪一个阶段的状态

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;

const int N = 1010;

int n, m, f[2][N];

int main()
{
    cin >> n >> m;
    int c = 0;
    for(int i = 1; i <= n; i ++){
        int v, w;
        cin >> v >> w;
        c = 1 - c;
        for(int j = 0; j <= m; j ++){
            f[c][j] = f[1 - c][j];
            if(j >= v)  f[c][j] = max(f[c][j], f[1 - c][j - v] + w);
        }
    }
    cout << f[c][m] << endl;


    return 0;

}

其实我们还可以将它优化为一维的滚动数组，但是这个时候滚动的方向就非常重要，01背包问题就需要从m~0循环，这样才能保证我当前i阶段用到的是i-1阶段的时候的状态(推f[j]时用的f[j - vi]用的是f[i-1, j - vi]时的状态)

例如，容量为10，有3个物体，

重量为5 1 2

价值为1 1 28

在递推第3阶段时，最后状态f[10]的值是由f[8] + 28和f[10]比较而来，此时我们要保证f[8]是上一个阶段的值，如果循环的顺序相反，就很难保证f[8]不会被更新过

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;

int f[N], n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        int v, w;
        cin >> v >> w;
        for(int j = m; j >= v; j --)
            f[j] = max(f[j], f[j - v] + w);
    }
    cout << f[m] << endl;


    return 0;

}

最后有一个Mod滚动数组，就是在当前阶段需要用到前面好几个状态的时候

例如f[n] = f[n - 1] + f[n - 2];我们就可以开一个f[3]

f[1] = 1;f[2] = 2;
for(int i = 3; i <= n; i ++){
    f[i % 3] = f[(i - 1) % 3] + f[(i - 2) % 3];
}

最后的最后，滚动数组是一种节约空间的办法。

3、完全背包问题

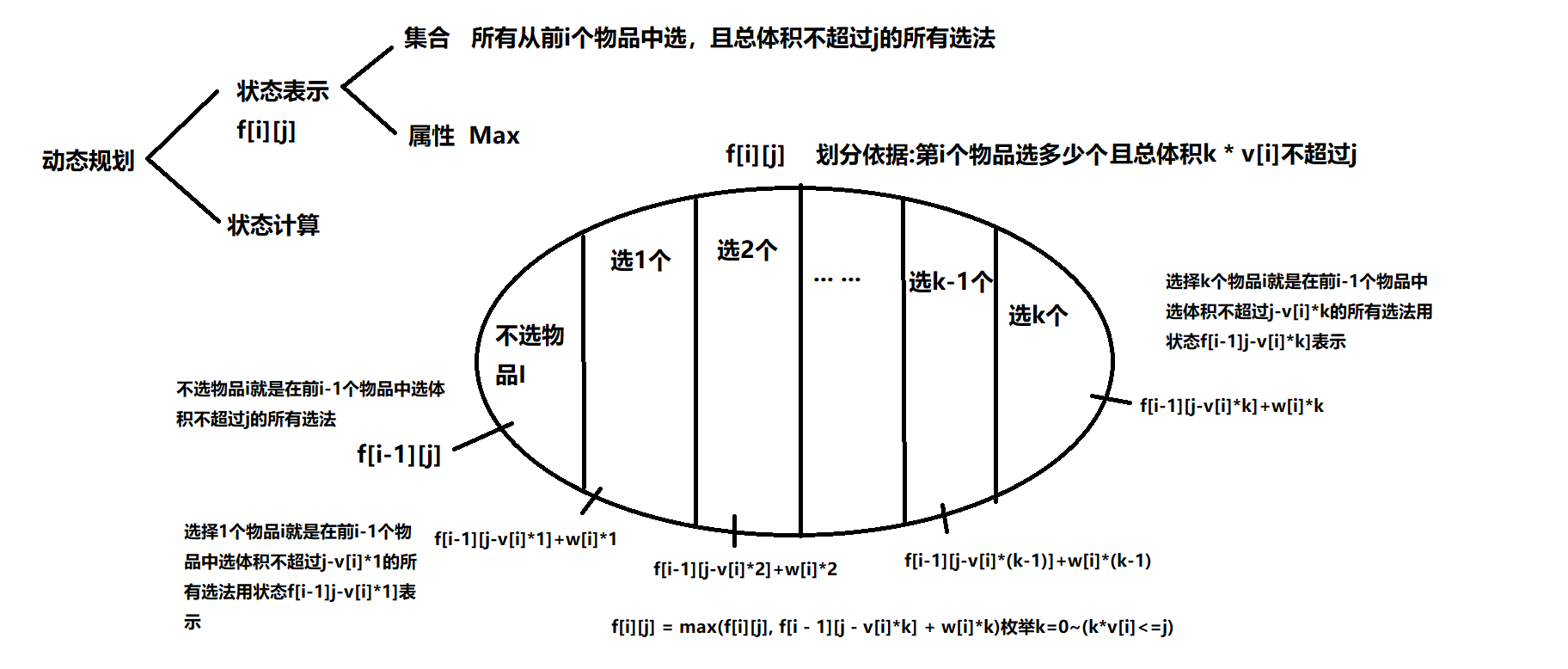
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;

int f[N][N], n, m;

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++){
        int v, w;
        scanf("%d%d", &v, &w);
        for(int j = 0; j <= m; j ++)
            for(int k = 0; k * v <= j; k ++)
                f[i][j] = max(f[i][j], f[i - 1][j - v * k] + w * k);
    }
    cout << f[n][m] << endl;


    return 0;

}

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;

int f[N][N], n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        int v, w;
        cin >> v >> w;
        for(int j = 0; j <= m; j ++){
            f[i][j] = f[i - 1][j];
            if(j >= v)  f[i][j] = max(f[i][j], f[i][j - v] + w);
        }
    }
    cout << f[n][m] << endl;


    return 0;

}

最后完全背包问题也可以用滚动数组来优化，但是枚举的顺序是和01背包相反的，因为完全背包用的都是当前状态从小到大枚举就可以保证每次f[j-v]都是最新的状态，虽然对于每个体积为j时，只在体积为j-v的基础上加上一个当前物品，但是体积为j-v的时候已经考虑过当前物品，并且已经取出了最大值，所以体积为j时如果可以更新最大值f[j]，也就是在对应的容量加上了最合适数目的当前物品。

例如，容量为10，有3个物体，

重量为5 1 2

价值为1 1 28

在递推第3阶段时，最后状态f[10]的值是由f[8] + 28和f[10]比较而来，此时我们要保证f[8]是已经充分得拿了合适数量的当前物品i，如果循环顺序从大到小，就不能保证当前体积已经充分拿了当前物品i

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;

int f[N], n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        int v, w;
        cin >> v >> w;
        for(int j = v; j <= m; j ++)
            f[j] = max(f[j], f[j - v] + w);
    }
    cout << f[m] << endl;


    return 0;

}

多重背包问题

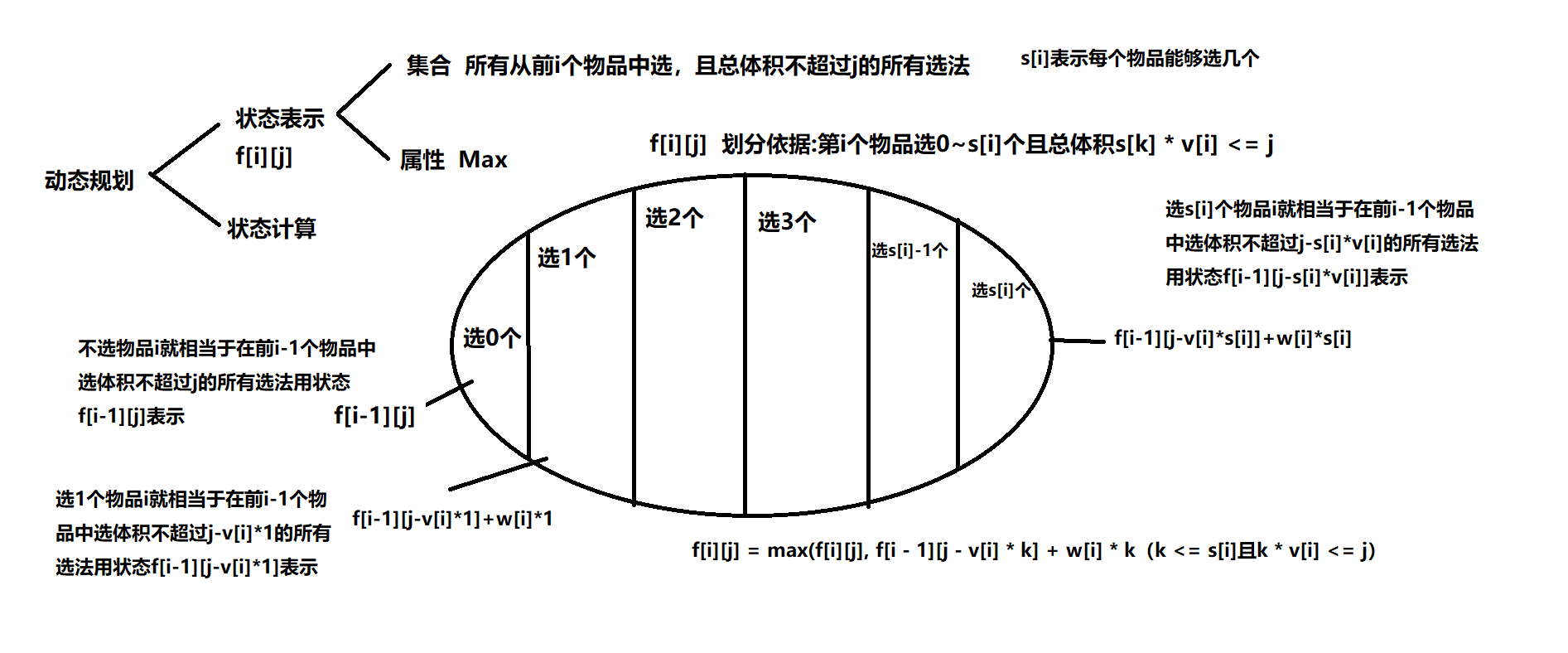
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;

const int N = 110;

int n, m, f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        int v, w, s;
        cin >> v >> w >> s;
        for(int j = 0; j <= m; j ++)
            for(int k = 0; k <= s && k * v <= j; k ++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v] + k * w);
    }
    cout << f[n][m] << endl;


    return 0;

}

二进制优化

首先多重背包可以拆分成完全背包和01背包来解

如果题目给的物品的个数大于等于当前体积能装的物品个数那么当成完全背包来解，如果题目给的物品的个数小于当前体积能装的物品个数那么就需要将当前物品当成s[i]个01背包来解
比如体积为8时
物品   A    B
体积   1    4
个数   3    10
对于物品A来说实际能装8个但是物品数量只有3所以需要将物品A当成3个01背包来解，但是对于物品B体积为8时只能装2个但是物品数量有10个所以可以当成完全背包来解
然后对于01背包（其实完全背包应该也是一样把）可以用一个二进制优化
二进制优化就是将一个数拆成二进制的形式
比如体积为9 ： 可以拆成1， 2， 4如果要组成9就再加一个9-7=2，这样就一个组成01背包的每一种选择比如要装8个物品就拿2个a[i]4个a[i]2个a[i]

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;

const int N = 2010;

int n, m, s, f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        int v, w, s;
        cin >> v >> w >> s;
        for(int k = 1; k <= s; k *= 2){
            for(int j = m; j >= k * v; j --)
                f[j] = max(f[j], f[j - k * v] + w * k);
            s -= k;
        }
        if(s)
            for(int j = m; j >= s * v; j --)
                f[j] = max(f[j], f[j - s * v] + s * w);
    }
    cout << f[m] << endl;


    return 0;

}

emmmm。。。单调队列优化，以后来补

分组背包问题

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 110;

int f[N], n, m, v[N], w[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        int x;
        cin >> x;
        for(int j = 0; j < x; j ++) cin >> v[j] >> w[j];
        for(int j = m; j >= 0; j --)
            for(int k = 0; k < x; k ++)
                if(j >= v[k])   f[j] = max(f[j], f[j - v[k]] + w[k]);


    }
    cout << f[m] << endl;

    return 0;

}

采药

emmm，模型就是01背包

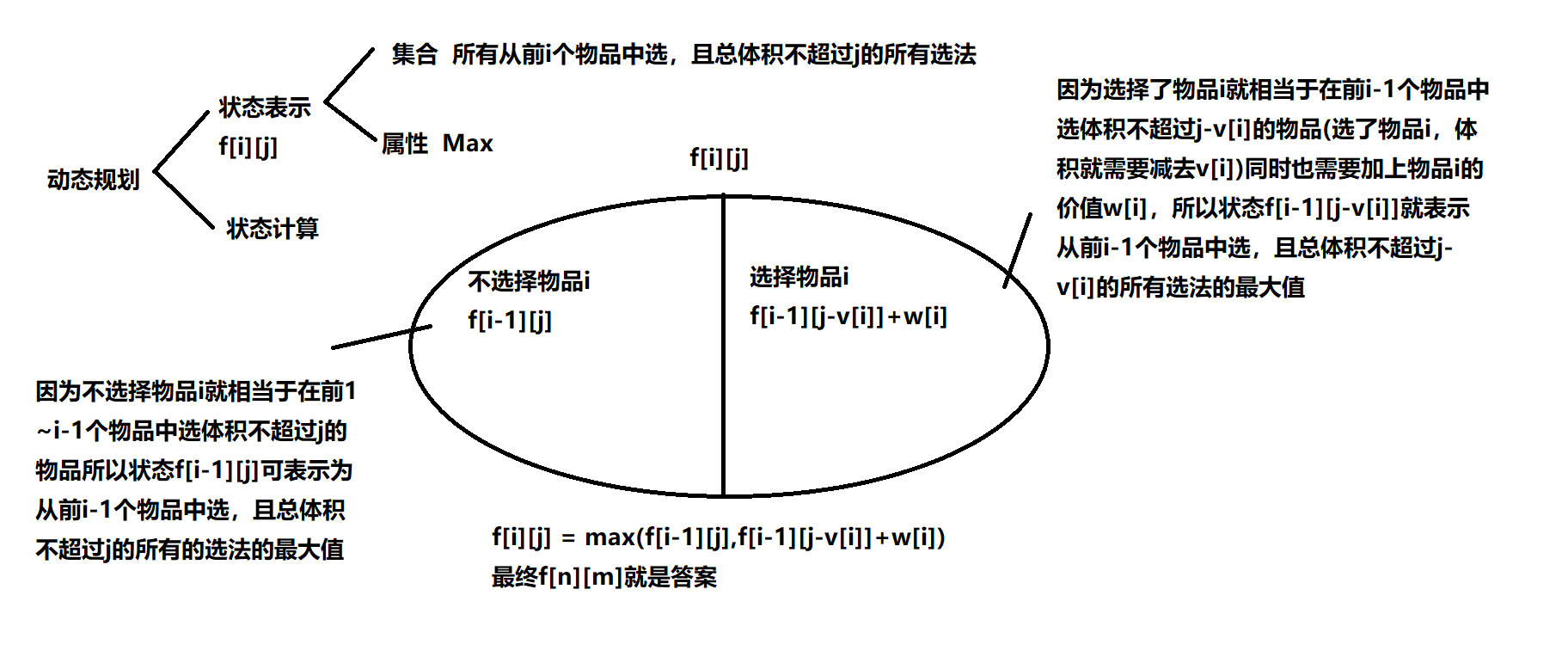
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;

int n, m;
int f[N];

int main()
{
    scanf("%d%d", &m, &n);
    for(int i = 0; i < n; i ++){
        int v, w;
        cin >> v >> w;
        for(int j = m; j >= v; j --){
            f[j] = max(f[j], f[j - v] + w);
        }
    }


    cout << f[m] << endl;

    return 0;

}

装箱问题

emmm，要让箱子的剩余体积最小，那么就要让装进去的体积最大，所以物品的价值就是体积还是01背包

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 20010;

int f[N], n, m;

int main()
{
    scanf("%d%d", &m, &n);
    for(int i = 0; i < n; i ++){
        int v;
        scanf("%d", &v);
        for(int j = m; j >= v; j --)
            f[j] = max(f[j], f[j - v] + v);
    }


    cout << m - f[m] << endl;

    return 0;

}

数字组合

emmm，01背包求方案数

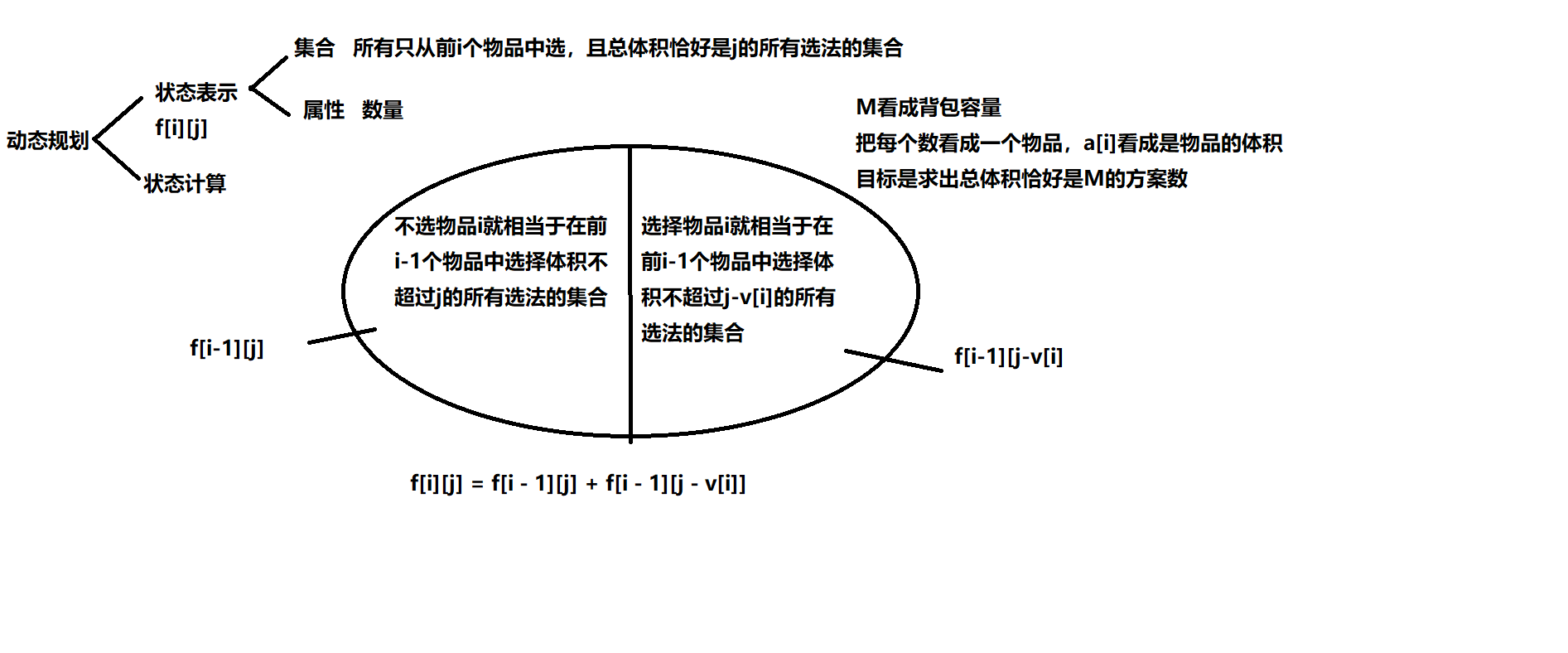
#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 10010;

int n, f[N], m;

int main()
{
    cin >> n >> m;
    f[0] = 1;
    for(int i = 1; i <= n; i ++){
        int v;
        cin >> v;
        for(int j = m; j >= v; j --)
            f[j] += f[j - v];
    }
    cout << f[m] << endl;


    return 0;

}

买书

emmmm,完全背包求方案数

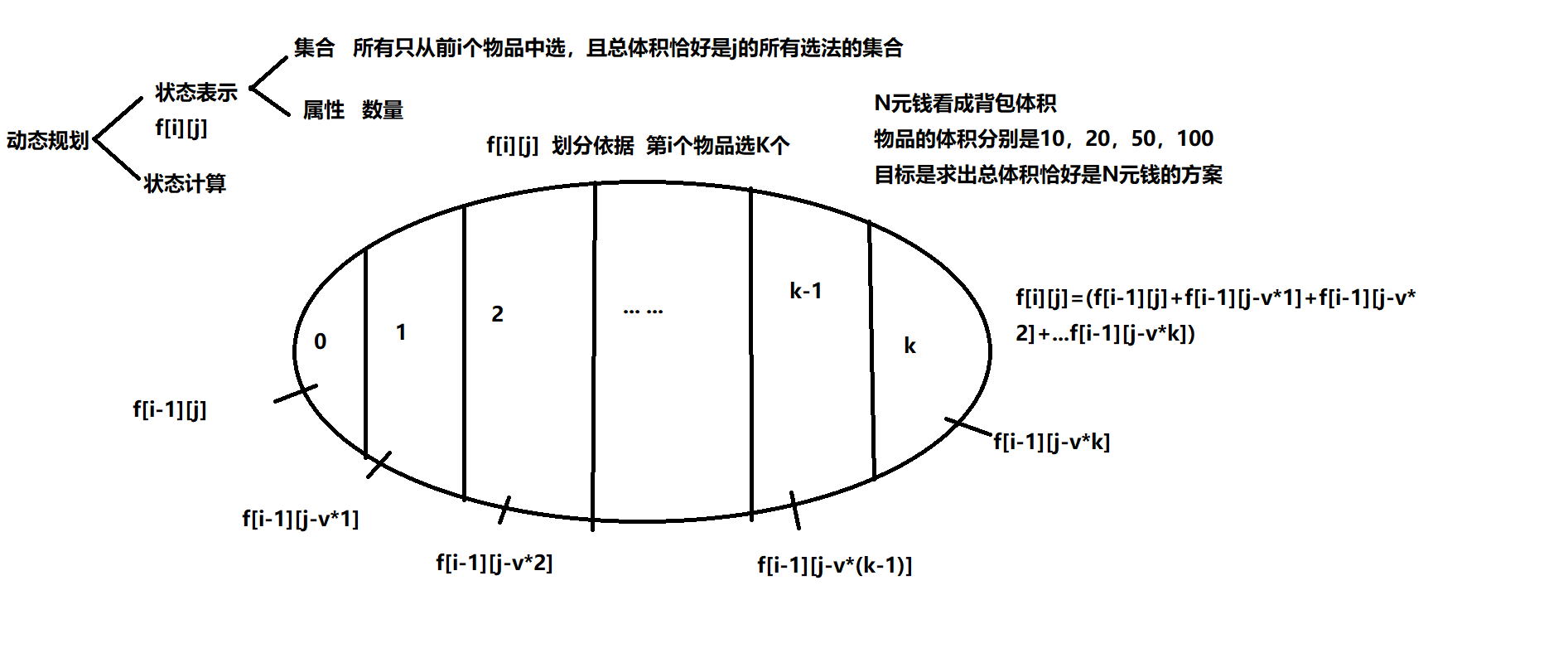
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;

int f[N], n;
int v[5] = {10, 20, 50, 100};

int main()
{
    cin >> n;
    f[0] = 1;
    for(int i = 0; i < 4; i ++)
        for(int j = v[i]; j <= n; j ++)
            f[j] += f[j - v[i]];
    cout << f[n] << endl;


    return 0;

}

货币系统

emmmm....完全背包求方案数

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 3010;

long long f[N], n, m;

int main()
{
    cin >> n >> m;
    f[0] = 1;
    for(int i = 1; i <= n; i ++){
        int v;
        cin >> v;
        for(int j = v; j <= m; j ++)
            f[j] += f[j - v];
    }
    cout << f[m] << endl;


    return 0;

}

货币系统

性质1：a1,a2,...,an一定都可以被表示出来
性质2:在最优解中，b1,b2,...,bm一定都是从a1,a2,...,an中选择的
性质3:b1,b2,...,bm一定不能被其它bi表示出来
emmmm，具体证明请参考y总提高课

当一种货币可以被其它货币表示的时候，那么当它被需要被某一中货币表示的时候，就可以用那些货币代替之，也就是这种货币可以去掉

先做一遍完全背包求方案数，当一种货币的方案数为1时，也就是只能被自己表示的时候就是一个答案

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 110, M = 25010;

int f[M], a[N], n, T;

int main()
{
    cin >> T;
    while(T -- ){
        scanf("%d", &n);
        for(int i = 1; i <= n; i ++)    scanf("%d", &a[i]);

        sort(a + 1, a + 1 + n);
        int res = 0, m = a[n];
        memset(f, 0, sizeof f);
        for(int i = 1; i <= n; i ++){
            if(!f[a[i]])    res ++;
            f[a[i]] = 1;
            for(int j = a[i]; j <= m; j ++)
                f[j] += f[j - a[i]];
        }
        cout << res << endl;
    }

    return 0;
}

庆功会

emmmm…模型就是多重背包

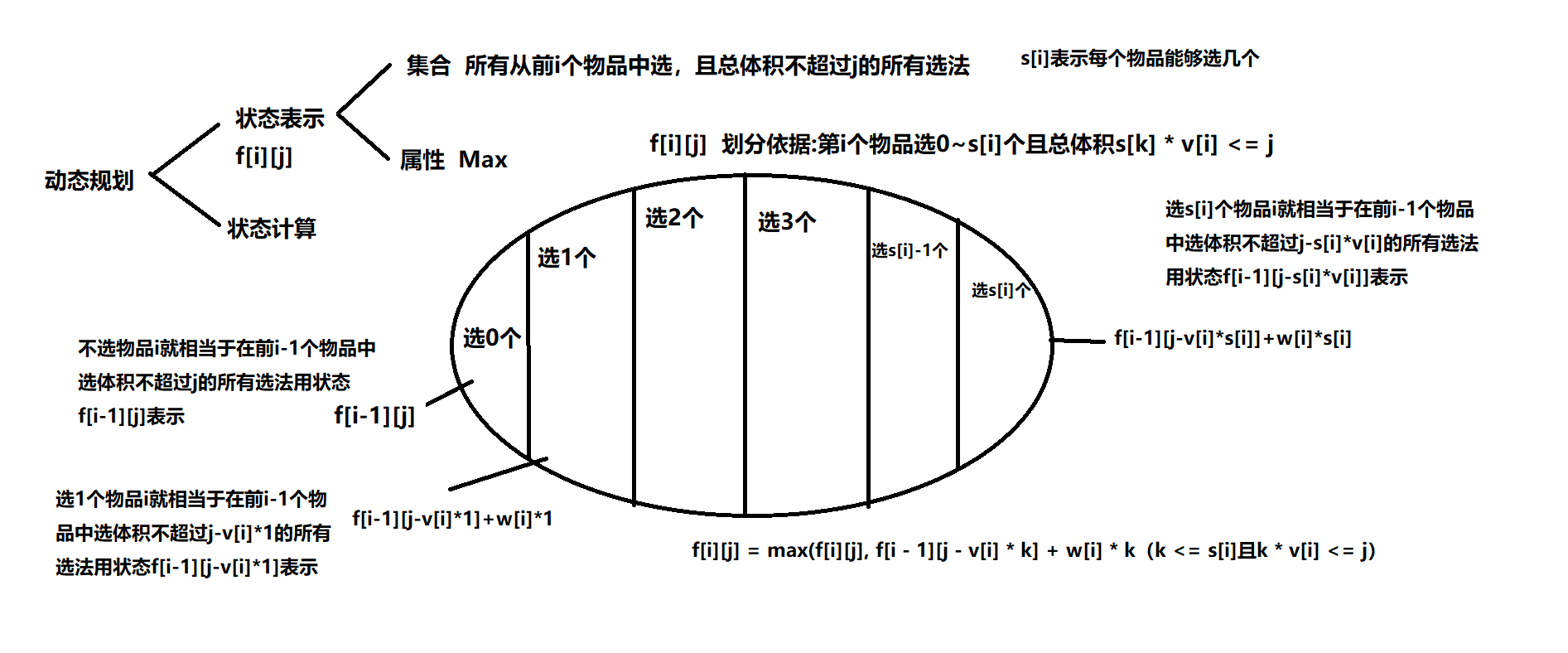
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 6010;

int f[N], n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        int v, w, s;
        cin >> v >> w >> s;
        for(int k = 1; k <= s; k *= 2){
            for(int j = m; j >= k * v; j --)
                f[j] = max(f[j], f[j - k * v] + k * w);
            s -= k;
        }
        if(s)
            for(int j = m; j >= s * v; j --)
                f[j] = max(f[j], f[j - s * v] + s * w);
    }
    cout << f[m] << endl;

    return 0;
}

混合背包问题

emmmm…01背包就是多重背包在物品数量为1时的情况，再一个就是注意完全背包和01背包的循环方式不同

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;

int n, m, f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        int v, w, s;
        cin >> v >> w >> s;
        if(!s)
            for(int j = v; j <= m; j ++)
                f[j] = max(f[j], f[j - v] + w);
        else{
            if(s == -1) s = 1;
            for(int k = 1; k <= s; k *= 2){
                for(int j = m; j >= k * v; j --)
                    f[j] = max(f[j], f[j - k * v] + k * w);
                s -= k;
            }
            if(s)
                for(int j = m; j >= s * v; j --)
                    f[j] = max(f[j], f[j - s * v] + s * w);
        }
    }
    cout << f[m] << endl;

    return 0;
}

二维费用的背包问题

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;

const int N = 1010;

int f[N][N], V, M, n;

int main()
{
    cin >> n >> V >> M;
    for(int i = 1; i <= n; i ++){
        int v, m, w;
        cin >> v >> m >> w;
        for(int j = V; j >= v; j --)
            for(int k = M; k >= m; k --)
                f[j][k] = max(f[j][k], f[j - v][k - m] + w);
    } 
    cout << f[V][M] << endl;

    return 0;
}

潜水员

#include<iostream>
#include<cstring>

using namespace std;

const int N = 22, M = 80;

int f[N][M], x, y, n;

int main()
{
    cin >> x >> y >> n;
    memset(f, 0x3f, sizeof f);
    f[0][0] = 0;

    for(int i = 1; i <= n; i ++){
        int v, w, m;
        cin >> v >> m >> w;
        for(int j = x; j >= 0; j --)
            for(int k = y; k >= 0; k --)
                f[j][k] = min(f[j][k], f[max(0, j - v)][max(0, k - m)] + w);
    }
    cout << f[x][y] << endl;

    return 0;
}

背包问题求具体方案

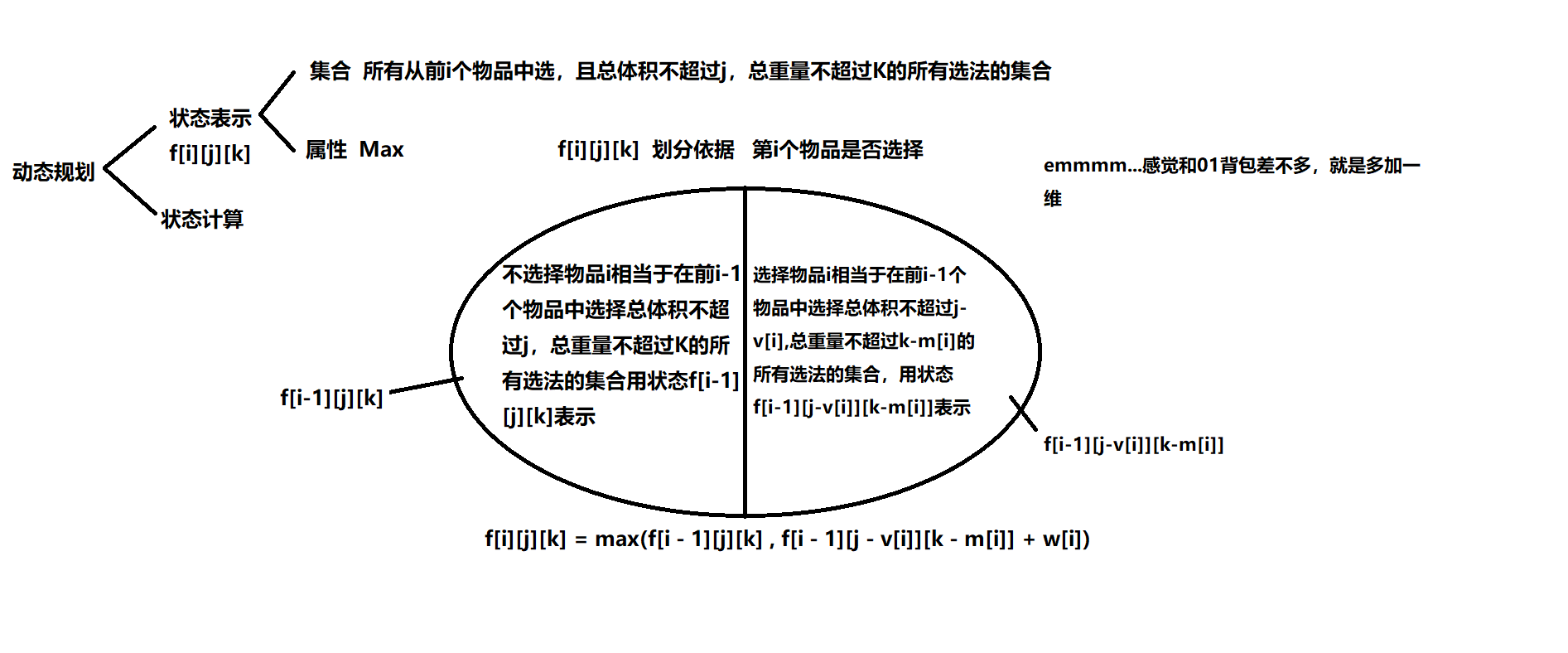
emmm…01背包求具体方案

先考虑状态转移方程
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
可以发现状态f[i][j]由f[i-1][j](不选物品i)和f[i-1][j-v[i]]+w[i](选择了物品i)转移而来
那么求具体方案时可以枚举每个物品的2种情况：选或者是不选
如果不选物品i就相当于状态f[i][j] = f[i-1][j](f[i][j]由状态f[i-1][j]转移过来),同时也相当于在前i - 1个物品中选择体积为j的物品所以最优解中体积不需要减去物品i的体积
如果选择了物品i就相当于f[i][j] = f[i - 1][j - v[i]] + w[i](f[i][j]由状态f[i-1][j - v[i]] + w[i]转移过来),同时也相当于在前i - 1个物品中选择体积为j - v[i]的物品所以最优解中体积需要减去物品i的体积
然后还有一种情况就是f[i][j] = f[i - 1][j - v[i]] + w[i] = f[i - 1][j]，这种情况说明物品可选可不选
考虑到要字典序最小，所以可以倒着做一遍01背包，然后正着枚举每个物品，同时为保证字典序最小，第3中情况必须选来保证字典序最小
求具体方案的时候需要用到每个物品的决策，所以不能用滚动数组优化（滚动数组优化会覆盖前i-1种物品的状态）

#include<iostream>
#include<cstring>

using namespace std;

const int N = 1010;

int v[N], w[N], f[N][N], n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)    cin >> v[i] >> w[i];

    for(int i = n; i >= 1; i --)
        for(int j = 0; j <= m; j ++){
            f[i][j] = f[i + 1][j];
            if(j >= v[i])   f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }

    int j = m;
    for(int i = 1; i <= n; i ++){
        if(j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]){
            cout << i << ' ';
            j -= v[i];
        }
    }

    return 0;
}

机器分配

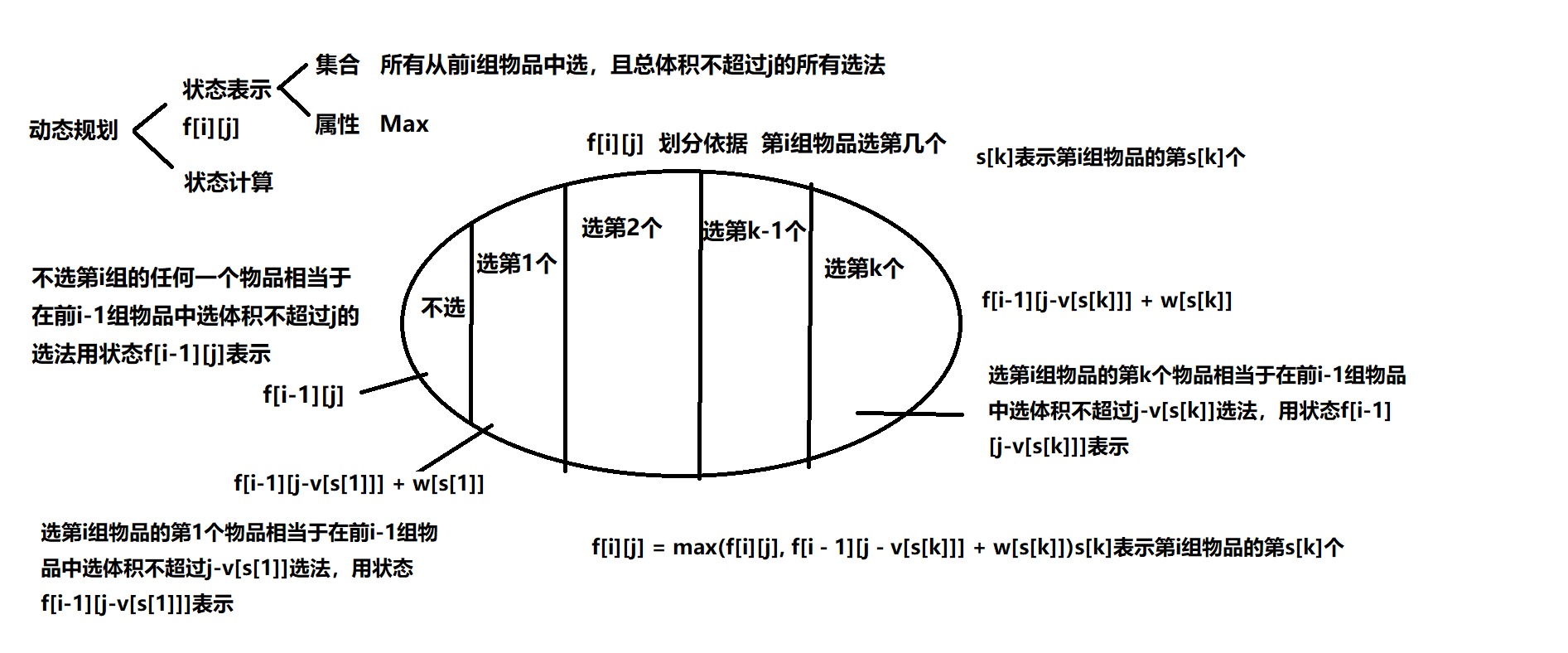
emmm..分组背包求具体方案(和01背包差不多吧)

先考虑状态转移方程
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i][k]] + w[i][k]);
可以发现状态f[i][j]由f[i-1][j](不选物品i)和f[i - 1][j - v[i][k]] + w[i][k](选择了i组物品的第k个)转移而来
然后求具体方案可以枚举每组物品有k + 1种情况：不选任何一种物品和选择第K个物品
如果不选第i组物品的任何一个物品就相当于状态f[i][j] = f[i-1][j](f[i][j]由状态f[i-1][j]转移过来),同时也相当于在前i - 1组物品中选择体积为j的物品所以最优解中体积不需要减去第i组物品的任何一个物品的体积
如果选择了物品i就相当于f[i][j] = f[i - 1][j - v[i][k]] + w[i][k](f[i][j]由状态f[i-1][j - v[i][k]] + w[i][k]转移过来),同时也相当于在前i - 1组物品中选择体积为j - v[i][k]的物品所以最优解中体积需要减去第i组物品的第k个物品的体积
然后还有一种情况就是f[i][j] = f[i - 1][j - v[i][k]] + w[i][k] = f[i - 1][j]，这种情况说明第i组物品可不选或者选择第k个物品
然后题目要求任意合法方案，就可以顺便循环顺序，第3种情况都可选
求具体方案的时候需要用到每个物品的决策，所以不能用滚动数组优化（滚动数组优化会覆盖前i-1组物品的状态）

#include<iostream>
#include<cstring>

using namespace std;

const int N = 20;

int f[N][N], n, m, a[N][N], g[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            cin >> a[i][j];

    for(int i = 1; i <= n; i ++)
        for(int j = 0; j <= m; j ++){
            f[i][j] = f[i - 1][j];
            for(int k = 1; k <= m; k ++)
                if(j >= k)  f[i][j] = max(f[i][j], f[i - 1][j - k] + a[i][k]);
        }

    int j = m;
    for(int i = n; i >= 1; i --)
        for(int k = 1; k <= m; k ++)
            if(j >= k && f[i][j] == f[i - 1][j - k] + a[i][k]){
                g[i] = k;
                j -= k;
                break;
            }

    cout << f[n][m] << endl;
    for(int i = 1; i <= n; i ++)    cout << i << ' ' << g[i] << endl;

    return 0;
}

背包问题求方案数

emmm…01背包求方案数

首先考虑状态转移方程
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i])
可以发现状态f[i][j]由f[i-1][j](不选物品i)和f[i-1][j-v[i]]+w[i](选择了物品i)转移而来
所以开一个数组g[N]来记录总方案数，初始化g数组为1，因为啥不选也是一种方案
如果状态f[i][j]由状态f[i - 1][j]转移而来，说明不选当前物品最大值更大，所以g[j]不变
如果状态f[i][j]由状态f[i - 1][j - v[i]] + w[i]转移而来，说明选了当前物品最大值发生了改变，g[j]就需要由g[j - v[i]]转移而来,g[j] = g[j - v[i]];
第3种情况就是f[i - 1][j] == f[i - 1][j - v[i]] + w[i] 说明选当前物品和不选当前物品最大值一样，那么g[j]就可以同时由g[j - v[i]]和g[j]转移来g[j] = g[j] + g[j - v[i]];

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;

const int N = 1010, mod = 1e9 + 7;

int f[N], g[N], n, m;

int main()
{
    scanf("%d%d", &n, &m);
    memset(f, -0x3f, sizeof f);
    g[0] = 1, f[0] = 0;
    // for(int j = 0; j <= m; j ++)    g[j] = 1;
    for(int i = 1; i <= n; i ++){
        int v, w;
        cin >> v >> w;

        for(int j = m; j >= v; j --){
            int maxv = max(f[j], f[j - v] + w);
            int cnt = 0;
            if(maxv == f[j])    cnt += g[j] % mod;
            if(maxv == f[j - v] + w)    cnt += g[j - v] % mod;
            g[j] = cnt % mod;
            f[j] = maxv;
        }
        for(int j = 0; j <= m; j ++)    cout << g[j] << " ";
        cout << endl;


    }

    int res = f[m], cnt = 0;
    for(int i = 1; i <= m; i ++)
        if(f[i] == res)
            cnt = (cnt + g[i]) % mod;

    cout << cnt << endl;

    return 0;
}

金明的预算方案

emmm…具体请参考y总的题解和y总的视频课啦

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;
#define v first
#define w second
typedef pair < int , int > pii;

const int N = 70, M = 32010;

int f[M], n, m;
pii a[N];
vector < pii > g[N];

int main()
{
    scanf("%d%d", &m, &n);
    for(int i = 1; i <= n; i ++){
        int v, w, p;
        cin >> v >> w >> p;
        if(!p)  a[i] = {v, v * w};
        else    g[p].push_back({v, v * w});
    }
    for(int i = 1; i <= n; i ++)
        if(a[i].v)
            for(int j = m; j >= 0; j -- )
                for(int k = 0; k < 1 << g[i].size(); k ++){
                    int v = a[i].v, w = a[i].w;
                    for(int u = 0; u < g[i].size(); u ++)
                        if(k >> u & 1){
                            v += g[i][u].v;
                            w += g[i][u].w;
                        }
                    if(j >= v)  f[j] = max(f[j], f[j - v] + w);
                }
    cout << f[m] << endl;
    return 0;
}

有依赖的背包问题

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 110, M = 200 + 10;

int h[N], ne[M], e[M], idx;
int n, f[N][N], root, w[N], m, v[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

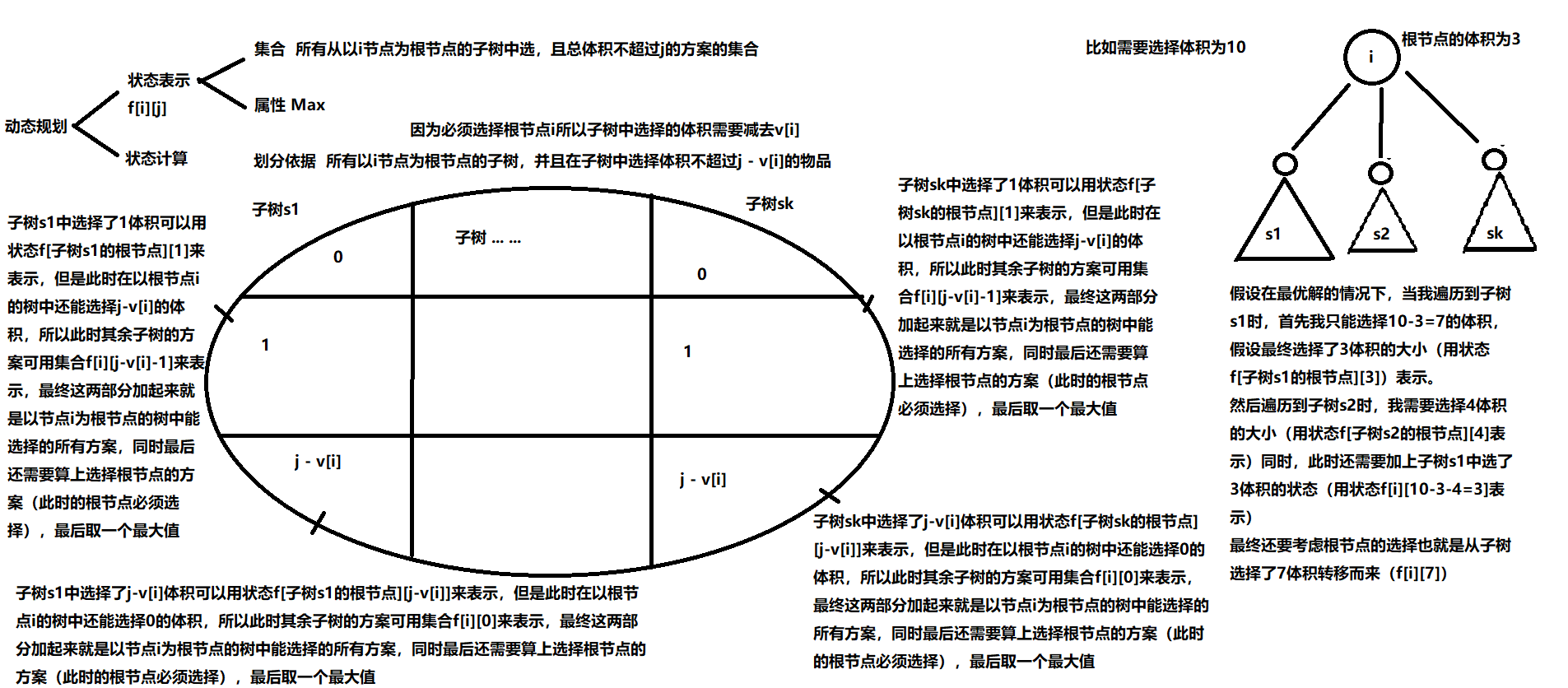
void dfs(int u)
{
    for(int i = h[u]; ~i; i = ne[i]){
        int ver = e[i];

        dfs(ver);// 先遍历子节点，先算子状态的值，然后回溯算大状态的值
        for(int j = m - v[u]; j >= 0; j --)// 因为必须考虑根节点所以必须从m-根节点的体积开始循环
            for(int k = 0; k <= j; k ++)
                f[u][j] = max(f[u][j], f[u][j - k] + f[ver][k]);
    }
    for(int j = m; j >= v[u]; j --) f[u][j] = f[u][j - v[u]] + w[u];// 考虑根节点的情况（此时必须选择）
    for(int j = v[u] - 1; j >= 0; j -- )    f[u][j] = 0;
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for(int i = 1; i <= n; i ++){
        int p;
        cin >> v[i] >> w[i] >> p;
        if(p == -1) root = i;
        else add(p, i);
    }

    dfs(root);

    cout << f[root][m] << endl;

    return 0;
}

能量石
emmmm…下次来补吧